Nomogramas para el predimensionamiento económico de muros de contención de tierras de hormigón armado

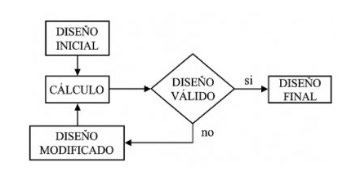
Los muros de contención son una de las estructuras más habituales en ingeniería civil y edificación, y el hormigón armado es el material predominante en la construcción de muros en ménsula. El diseño de este tipo de estructuras implica una interacción compleja entre el terreno y la propia estructura con el fin de garantizar su estabilidad de manera segura y rentable. El proceso de diseño suele comenzar con una geometría inicial obtenida a partir de reglas empíricas de prediseño o de referencias basadas en estudios de casos previos (MOPT, 1984; Calavera, 2001). A continuación, se lleva a cabo un análisis preliminar en el que se consideran los requisitos de estabilidad, resistencia y durabilidad. Si la propuesta inicial no cumple alguno de estos criterios o lo hace con márgenes de seguridad excesivos, se realizan ajustes y se repite el proceso (véase la Figura 1).

A medida que se avanza hacia una solución estructuralmente adecuada, esta metodología basada en prueba y error presenta importantes limitaciones: carece de objetividad en la selección de dimensiones y materiales y su eficiencia económica depende en gran medida del criterio y la experiencia del proyectista. No obstante, en el diseño de infraestructuras no basta con satisfacer los requisitos de seguridad, calidad y funcionalidad, también es necesario abordar el proceso desde una perspectiva de eficiencia de costes. Para ello, herramientas como la optimización heurística se han consolidado como recursos eficaces para afrontar este tipo de retos (Carbonell et al., 2011; Penadés-Plà et al., 2018). Asimismo, el uso de metamodelos representa otra vía prometedora para mejorar la eficiencia y la objetividad del diseño (Yepes-Bellver et al., 2025).

La nomografía, introducida por Maurice d’Ocagne en 1884, fue una herramienta fundamental para la resolución de problemas de ingeniería mediante el uso de nomogramas o ábacos durante el siglo XX (Adams, 1964). Su precisión y utilidad permitieron a científicos y proyectistas abordar problemas complejos con eficacia. Sin embargo, con la llegada y popularización de las calculadoras de mano y los ordenadores, su uso fue disminuyendo progresivamente. No obstante, la nomografía sigue teniendo un valor significativo, especialmente en el ámbito educativo (Martínez-Pagán y Roschier, 2022).

En los últimos años, se ha observado un renovado interés por los nomogramas, impulsado por el desarrollo de programas de código abierto que permiten crearlos de forma rápida, precisa y accesible, sin necesidad de tener conocimientos matemáticos avanzados. Los docentes de escuelas de ingeniería reconocen su utilidad pedagógica, lo que garantiza su vigencia a pesar del avance tecnológico (Blight et al., 2025).

La incorporación de la nomografía como herramienta digital en la enseñanza de la ingeniería y las ciencias responde a varias razones. En primer lugar, al tratarse de un recurso poco habitual, capta la atención del alumnado. En segundo lugar, fomenta habilidades clave relacionadas con el diseño y la interpretación de nomogramas, que se mantienen vivas en el entorno académico. En tercer lugar, permite visualizar fórmulas complejas a través de la representación gráfica de sus variables y relaciones. Por último, resulta especialmente útil para quienes comprenden de forma intuitiva las representaciones gráficas.

En la actualidad, la nomografía se beneficia de cálculos actualizados y del uso de herramientas de software avanzado y de código abierto, lo que facilita la generación de ábacos personalizados, precisos y eficientes para tareas que requieren cálculos repetitivos. Además, constituye una alternativa fiable en entornos en los que no se dispone de calculadoras ni de dispositivos electrónicos (Douglas y Danciu, 2020; Glasser y Doerfler, 2019).

Históricamente, una de las tareas más complejas en el ámbito de la nomografía era la construcción del nomograma, que requería una representación gráfica precisa y minuciosa. Esta etapa implicaba el trazado detallado de escalas, divisiones y mallas, lo que suponía un gran desafío técnico para los diseñadores. Esta dificultad fue uno de los factores que contribuyó al progresivo abandono de los nomogramas hacia finales del siglo XX, un proceso que se aceleró con la aparición de las calculadoras programables y los ordenadores personales, herramientas que ofrecían alternativas más rápidas y flexibles.

En el contexto del diseño estructural, los muros de contención, y en particular los muros en ménsula de hormigón armado, exigen alcanzar un equilibrio adecuado entre estabilidad, seguridad y coste. Los métodos tradicionales para su dimensionamiento, basados en procedimientos de ensayo y error, han demostrado su eficacia, aunque presentan ciertas limitaciones. Se trata de procesos subjetivos, altamente dependientes de la experiencia del ingeniero, y que pueden resultar poco eficientes desde el punto de vista económico. En este sentido, la nomografía, respaldada actualmente por herramientas de código abierto, se presenta como una alternativa valiosa para facilitar el aprendizaje de cálculos estructurales complejos y para apoyar la toma de decisiones durante el diseño final de los muros de contención.

El objetivo principal de este artículo es presentar un conjunto de nomogramas desarrollados para facilitar el diseño geométrico preliminar de muros de contención de hormigón armado y proporcionar una estimación fiable de su coste por metro lineal. Estas herramientas gráficas ofrecen una alternativa intuitiva y ágil a los métodos tradicionales basados en ensayo y error, y permiten a los proyectistas tomar decisiones con mayor rapidez y eficacia.

Además, el estudio incluye una serie de recomendaciones prácticas para optimizar el diseño, fruto de una investigación exhaustiva. Dichas recomendaciones tienen como objetivo mejorar la eficiencia estructural, reducir el consumo de materiales y maximizar la rentabilidad económica de estas estructuras.

Al integrar estas herramientas con una comprensión profunda del problema, este trabajo aspira a cerrar la brecha entre los métodos tradicionales de diseño y las técnicas modernas de cálculo, contribuyendo a establecer un procedimiento más objetivo, eficiente y económico para el diseño de muros de contención de hormigón armado.

En el estudio de Yepes et al. (2008), se aplicó el algoritmo Simulated Annealing (Kirkpatrick et al., 1983) para llevar a cabo un análisis paramétrico de muros de contención. En dicho trabajo se tuvieron en cuenta veinte variables de diseño y se evaluó el comportamiento estructural de los muros en distintas condiciones de empuje y capacidad. Como resultado, se obtuvieron 63 diseños optimizados, cuyos datos permitieron formular expresiones preliminares de diseño.

El presente trabajo amplía esta línea de investigación mediante el desarrollo de modelos lineales que permiten calcular variables geométricas clave en función de la altura del muro, el tipo de relleno y las condiciones del soporte. Estos modelos se han utilizado para elaborar nomogramas que simplifican el diseño preliminar con un enfoque centrado en la optimización de costes.

Las condiciones de diseño abarcan todos los estados límite que deben cumplir tanto la estructura del muro de contención como su cimentación. Antes de verificar estos estados límite, es necesario determinar la presión ejercida por el terreno, que depende directamente de las características del relleno y de las cargas superficiales. Esta presión se considera en el estado activo del terreno, según lo establecido por la teoría de Coulomb. En el caso de los muros de contención que se modelan como cuerpos rígidos, es imprescindible comprobar tres estados límite fundamentales: el vuelco, el deslizamiento y la presión del terreno. El análisis de estos estados se realiza mediante un procedimiento riguroso y claramente definido.

Paralelamente, el desarrollo de herramientas de código abierto basadas en el lenguaje de programación Python ha simplificado la generación de nomogramas, lo que facilita su construcción de manera rápida y precisa. En este estudio se ha utilizado el programa Pynomo (Roschier, 2022), una herramienta que permite crear nomogramas personalizados para el diseño preliminar de la geometría de los muros de contención. Este enfoque permite representar de manera eficiente las relaciones clave involucradas en el diseño de estas estructuras, de modo que los proyectistas puedan estimar los parámetros fundamentales en función de la altura del muro, el tipo de relleno y las condiciones de carga (véase la Figura 2).

Los nomogramas generados en este estudio están disponibles en formatos vectoriales PDF y EPS, lo que facilita su edición, refinamiento o rediseño posterior según las necesidades específicas del usuario final. Gracias a esta flexibilidad, pueden adaptarse con programas de diseño como Adobe Illustrator o Microsoft Visio, lo que garantiza una presentación clara y una integración eficaz en aplicaciones de ingeniería (Martínez-Pagán et al., 2023; Mottola y Cocconcelli, 2023). Esta metodología contribuye a consolidar el valor de los nomogramas propuestos como herramientas fiables y prácticas para el diseño preliminar de muros de contención y favorece soluciones estructurales optimizadas en términos de coste.

Para obtener más información sobre el uso del programa Pynomo, se recomienda visitar las páginas web http://pynomo.org/wiki/index.php/Pynomo_details y http://lefakkomies.github.io/pynomo-doc/installation/installation.html (Boulet et al., 2021), donde se pueden encontrar enlaces para descargar el programa, instrucciones sobre su uso, tutoriales y documentación esencial para su manejo.

La documentación básica proporciona toda la información necesaria para construir nomogramas, incluso para quienes no tienen experiencia previa en programación con Python (Doerfler, 2009). Es importante destacar la amplia variedad de nomogramas que pueden abordarse y generarse siguiendo estos conceptos fundamentales, así como su amplia aplicabilidad en diferentes disciplinas científicas e ingenieriles. Entre las disciplinas ingenieriles que pueden beneficiarse de estos nomogramas se encuentran la ingeniería civil, minera, energética, mecánica, hidráulica, etc. (Martínez-Pagán y Roschier, 2022; Mottola y Cocconcelli, 2023).

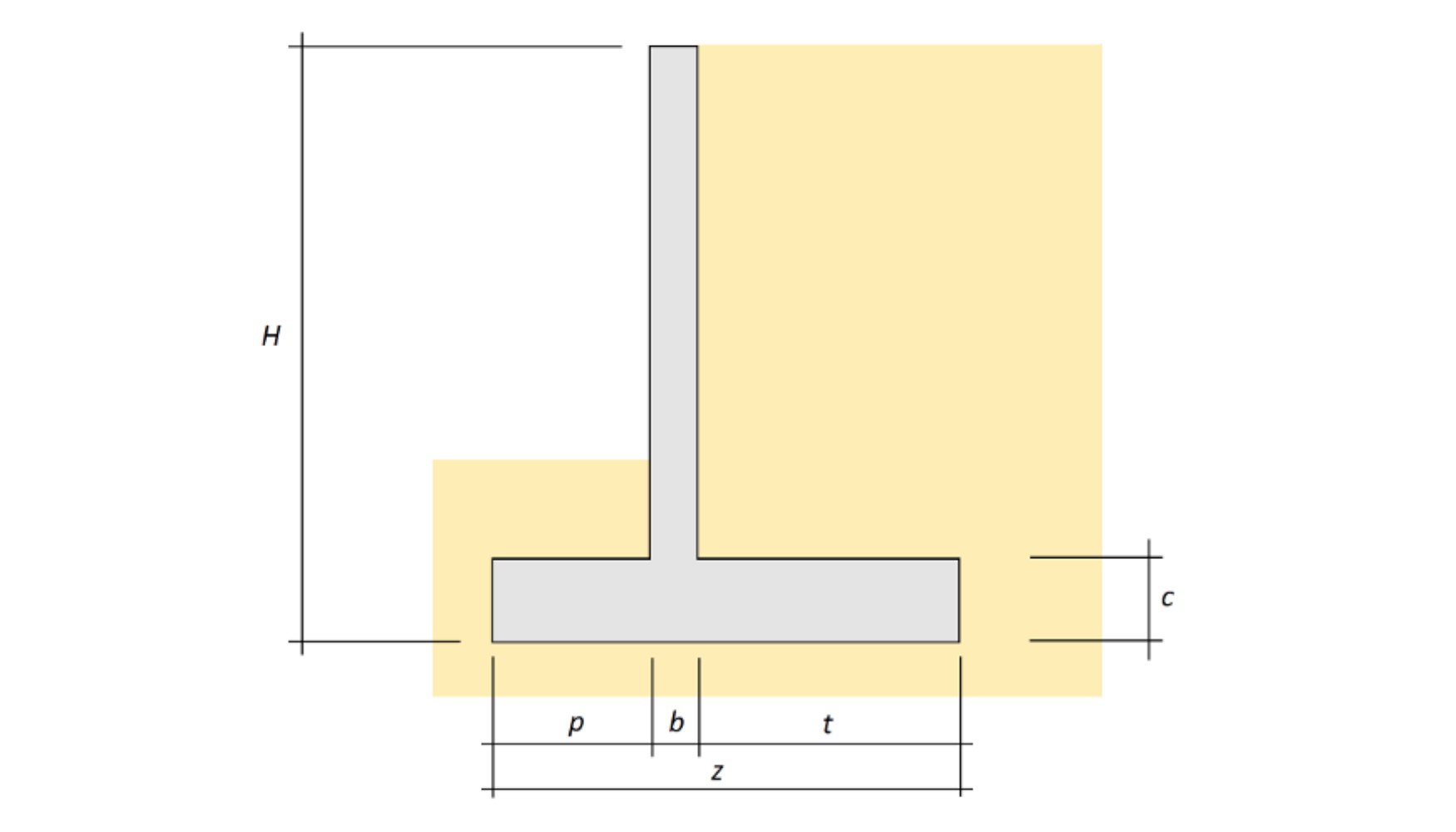
La siguiente sección presenta los nomogramas desarrollados específicamente para el diseño preliminar de muros de contención. Estas herramientas gráficas permiten estimar de manera rápida y sencilla los parámetros geométricos clave a partir de las variables fundamentales del diseño. Los altos coeficientes de correlación obtenidos en los modelos lineales utilizados confirman su eficacia para predecir con precisión las variables que definen las dimensiones geométricas de estos muros. En concreto, los modelos tienen en cuenta tres variables principales: la altura total del muro H (m), el peso específico del material de relleno γ (kN/m³) y la capacidad portante del terreno σ (MPa). Los nomogramas resultantes constituyen una herramienta fiable y funcional, ya que permiten realizar una estimación preliminar de forma ágil y mantienen una adecuada correlación con las soluciones optimizadas obtenidas mediante métodos más complejos.

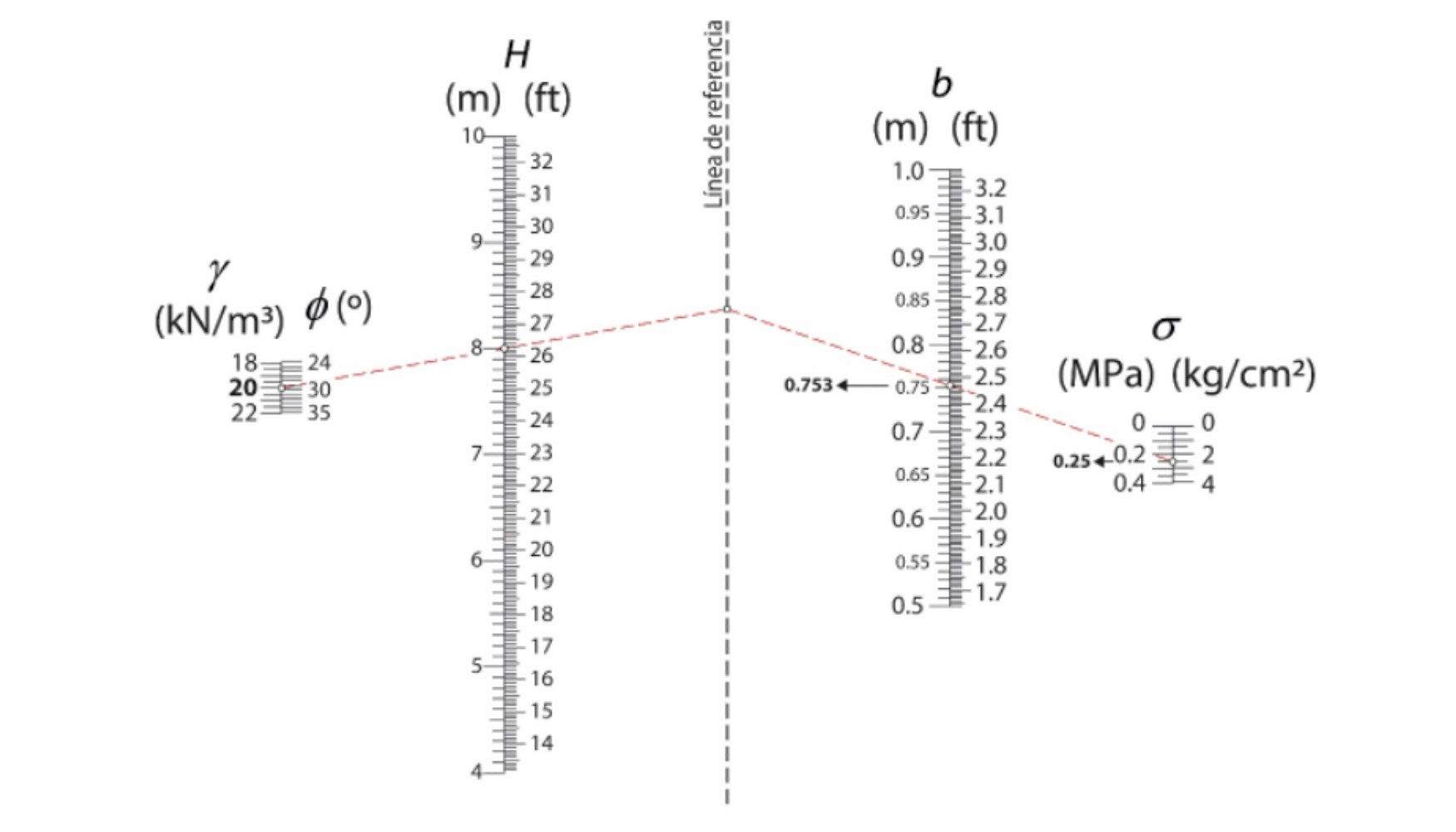
La Figura 3 muestra un nomograma que ilustra cómo varía el espesor del alzado del muro b en función de la altura total H. Esta herramienta gráfica permite estimar de forma intuitiva y rápida dicho espesor para distintas alturas de muro, lo que facilita la toma de decisiones en las primeras etapas del diseño. La relación mostrada en el nomograma se ajusta adecuadamente a las recomendaciones empíricas de prediseño, que sugieren que el espesor del alzado debería ser aproximadamente una décima parte de la altura del muro. Esta regla práctica es una referencia útil para los proyectistas a la hora de definir las dimensiones iniciales.

Además, el nomograma muestra el impacto del espesor del alzado causado por factores adicionales, como las propiedades del material de relleno y la capacidad portante del terreno. Aunque estos parámetros geotécnicos contribuyen a la variación del valor b, su influencia es secundaria en comparación con la altura total del muro, que sigue siendo la variable principal. A medida que aumenta la altura del muro, también debe incrementarse el espesor del alzado para garantizar su estabilidad estructural y una distribución adecuada de las cargas.

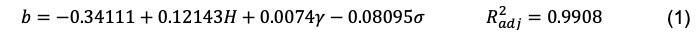
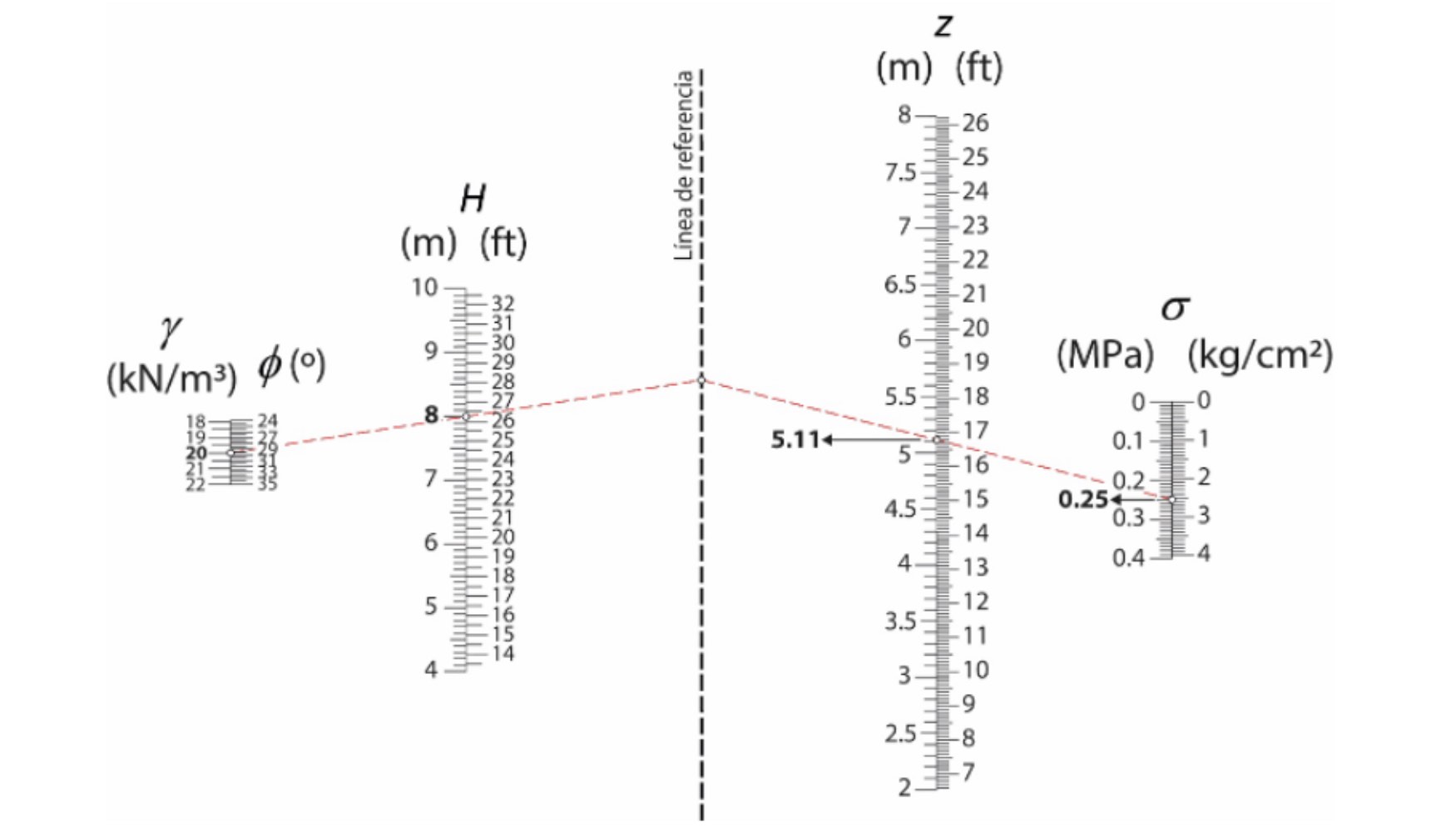
La Figura 4 muestra un nomograma para analizar la longitud de la zapata del muro. Los resultados indican que esta dimensión suele estar comprendida entre el 50% y el 60% de la altura total del muro, lo que proporciona una referencia práctica para las consideraciones preliminares del diseño.

La capacidad portante del terreno y el peso específico del material de relleno influyen en las variaciones de la longitud de la zapata, aunque su impacto es relativamente limitado. La variable que más influye en este parámetro es la altura total del muro (H), que determina las dimensiones que debe tener la zapata para garantizar la estabilidad de la estructura. Al analizar estas relaciones, se confirma que el nomograma es una herramienta eficaz para seleccionar diseños optimizados que consigan un equilibrio adecuado entre los requisitos de seguridad y la eficiencia en el uso de materiales.

Además, en la Figura 4 se observa que la capacidad portante del suelo influye más en la longitud de la zapata que en la Figura 3. Esta diferencia pone de manifiesto cómo las variaciones en las condiciones portantes del terreno pueden afectar significativamente a las dimensiones requeridas de la base y subraya la importancia de tener en cuenta las propiedades geotécnicas locales en el proceso de diseño. La ecuación (2) se ha utilizado para generar el nomograma de la Figura 4.

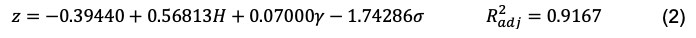
La Figura 5 muestra el nomograma que se utilizó para estimar la variación del canto de la zapata en función de la altura total del muro. Los resultados indican que esta dimensión suele estar comprendida entre el 7% y el 18% de la altura total del muro, lo que es comparable al espesor habitual del alzado. Esto sugiere una relación proporcional entre estos elementos estructurales.

Además, el nomograma subraya que, si bien factores como la capacidad portante del suelo y las propiedades del material de relleno podrían influir, la altura total del muro (H) sigue siendo la variable predominante que determina el canto de la zapata. Esta consistencia a lo largo de diferentes elementos estructurales refuerza la fiabilidad del método de diseño preliminar propuesto y proporciona una herramienta importante para optimizar el dimensionamiento de los muros de contención en las primeras etapas del diseño.

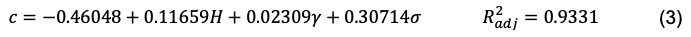
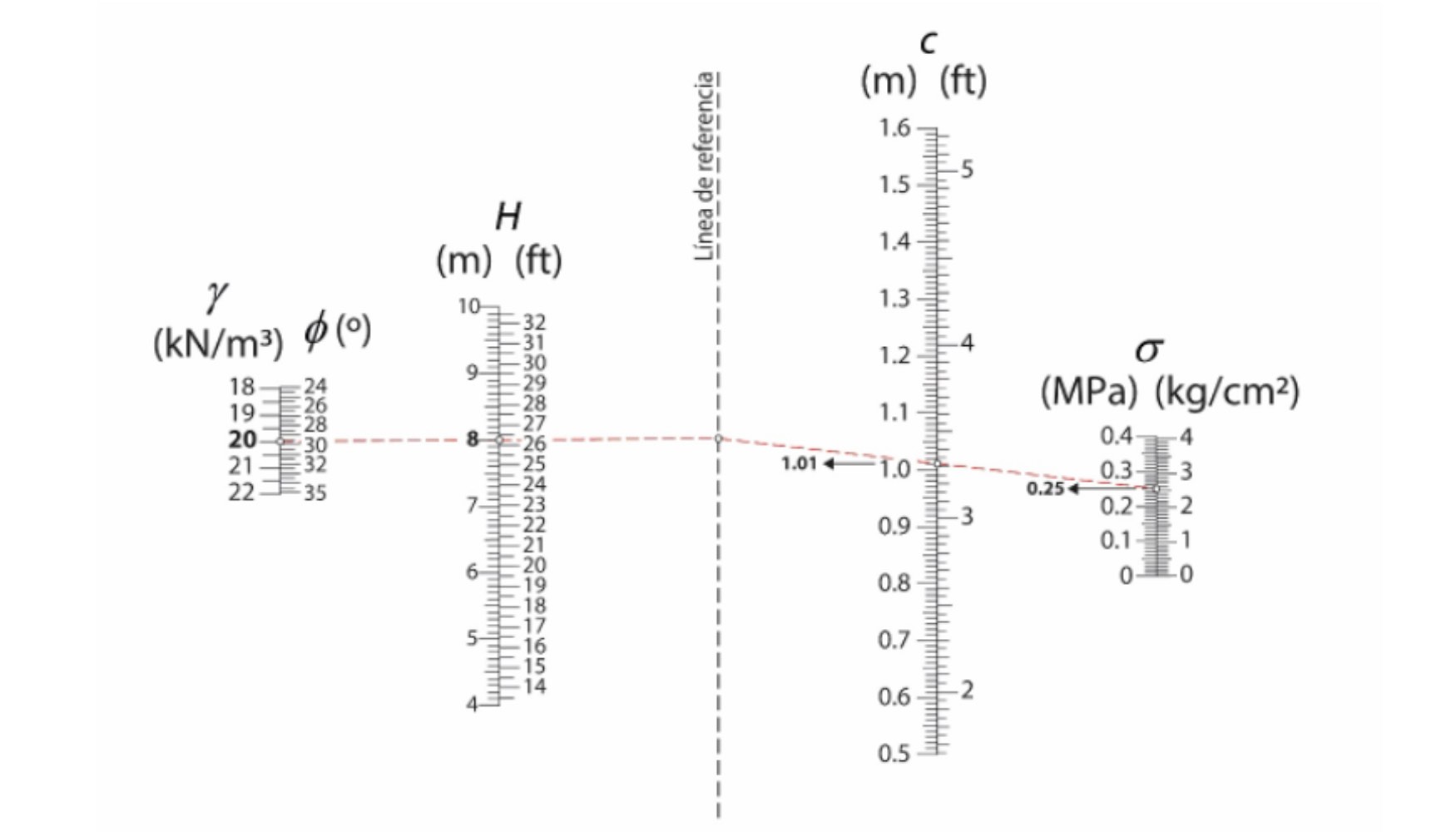
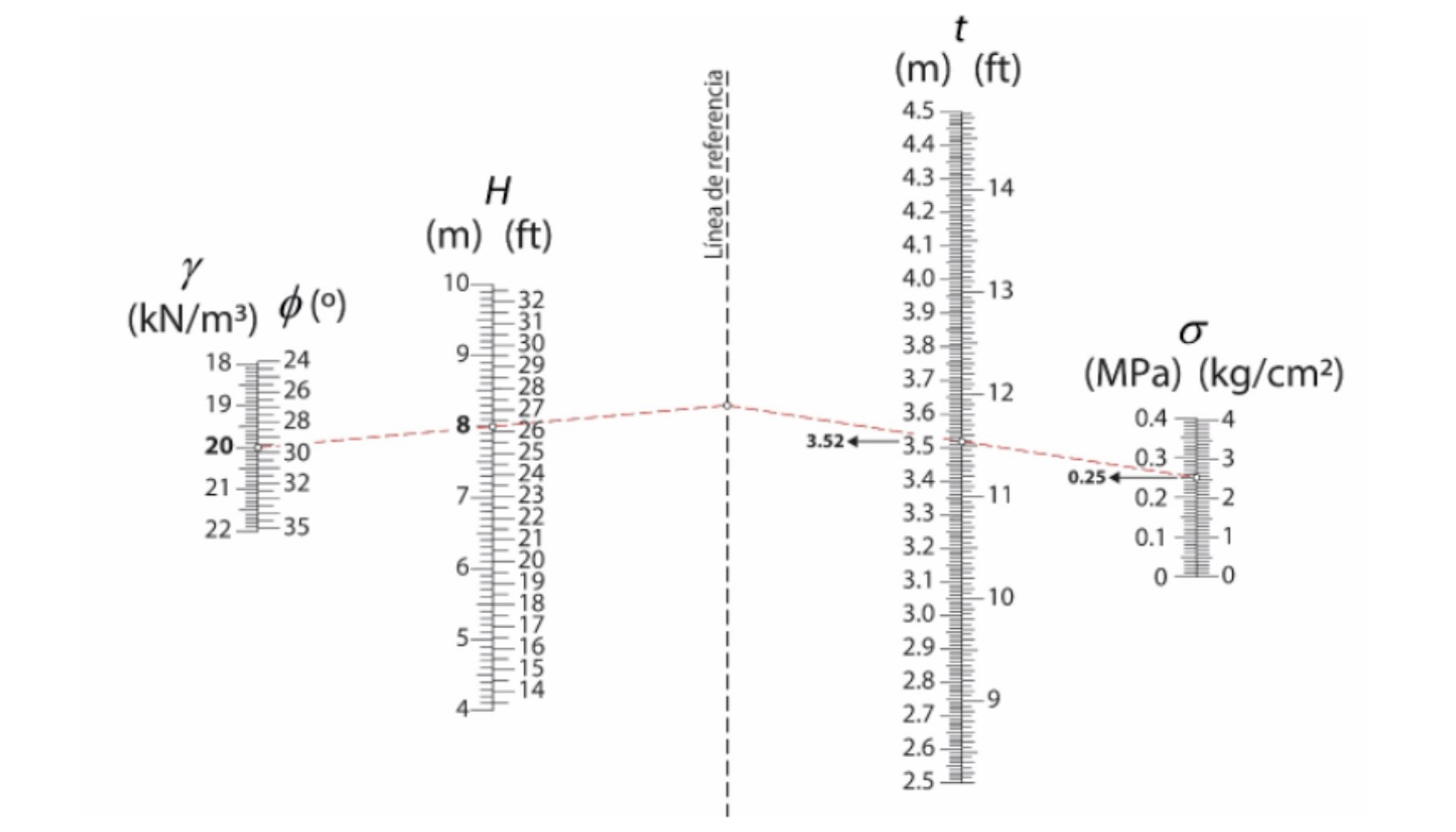
La Figura 6 muestra el nomograma que representa la variación de la longitud del talón (t) de la base en función de la altura del muro, el tipo de material de relleno y las condiciones portantes del suelo, según las conclusiones de Yepes et al. (2008). Los resultados revelan una clara tendencia en la relación entre la longitud del talón y la altura total del muro, que muestra cómo la geometría del pie se adapta a la necesidad de un mayor incremento estructural.

La proporción entre la longitud del talón (t) y la longitud de la zapata (z), expresada como t/z, tiende a disminuir a medida que aumenta la altura del muro. En estructuras más altas, se amplía la sección correspondiente al talón con el objetivo de desplazar el punto de equilibrio de la base, gestionar adecuadamente la presión ejercida por el terreno y satisfacer los requisitos de estabilidad. En la práctica, el cociente t/z es aproximadamente 0,80 para muros más cortos, mientras que se reduce a 0,50 para estructuras más altas. Esta tendencia subraya la necesidad de adaptar el diseño para distribuir mejor la carga y favorecer la estabilidad global del muro de contención.

Estos resultados ponen de manifiesto la importancia de optimizar las dimensiones de la base para garantizar la eficiencia estructural y la viabilidad económica del diseño. Al ajustar sistemáticamente la proporción entre el talón y la zapata en función de las propiedades del terreno y de la altura del muro, se puede conseguir un diseño más equilibrado que satisfaga los requisitos de estabilidad y capacidad portante. Este enfoque permite evitar el uso excesivo de materiales y promover soluciones constructivas más sostenibles y rentables.

Además, la Figura 6 subraya una influencia más pronunciada del peso unitario del material de relleno y de la capacidad portante del suelo en relación con los demás parámetros analizados en las figuras anteriores. Esto se hace evidente en los rangos de escala más amplios asignados a estas variables, en particular en relación con las de la Figura 3, lo que indica que las variaciones de estos parámetros influyen significativamente en la longitud del talón y subraya su papel crítico en el diseño de la zapata.

Basándose en los resultados de Yepes et al. (2008), se pueden establecer algunas conclusiones clave en relación con el coste de los muros de contención de hormigón armado. El coste total de un muro muestra una fuerte correlación (R² = 0,9705) con el valor de su altura total (H) elevada al cuadrado. En esta fórmula, la altura se define como la diferencia de elevación entre la parte superior del muro y la superficie de contacto de la zapata con el terreno. Asimismo, la capacidad portante del suelo reduce los costes totales, mientras que la presión horizontal que ejerce el terreno sobre el relleno posterior al muro también influye. Teniendo en cuenta los precios de mercado actuales, los diseños más eficientes en términos de coste incorporan de forma consistente aceros de alta resistencia (500 N/mm²) y, en la mayoría de los casos, hormigón con las características de resistencia más bajas permitidas (25 N/mm²). Resultados similares se pueden consultar para este tipo de muros con bajas emisiones de CO₂ (Yepes et al., 2012).

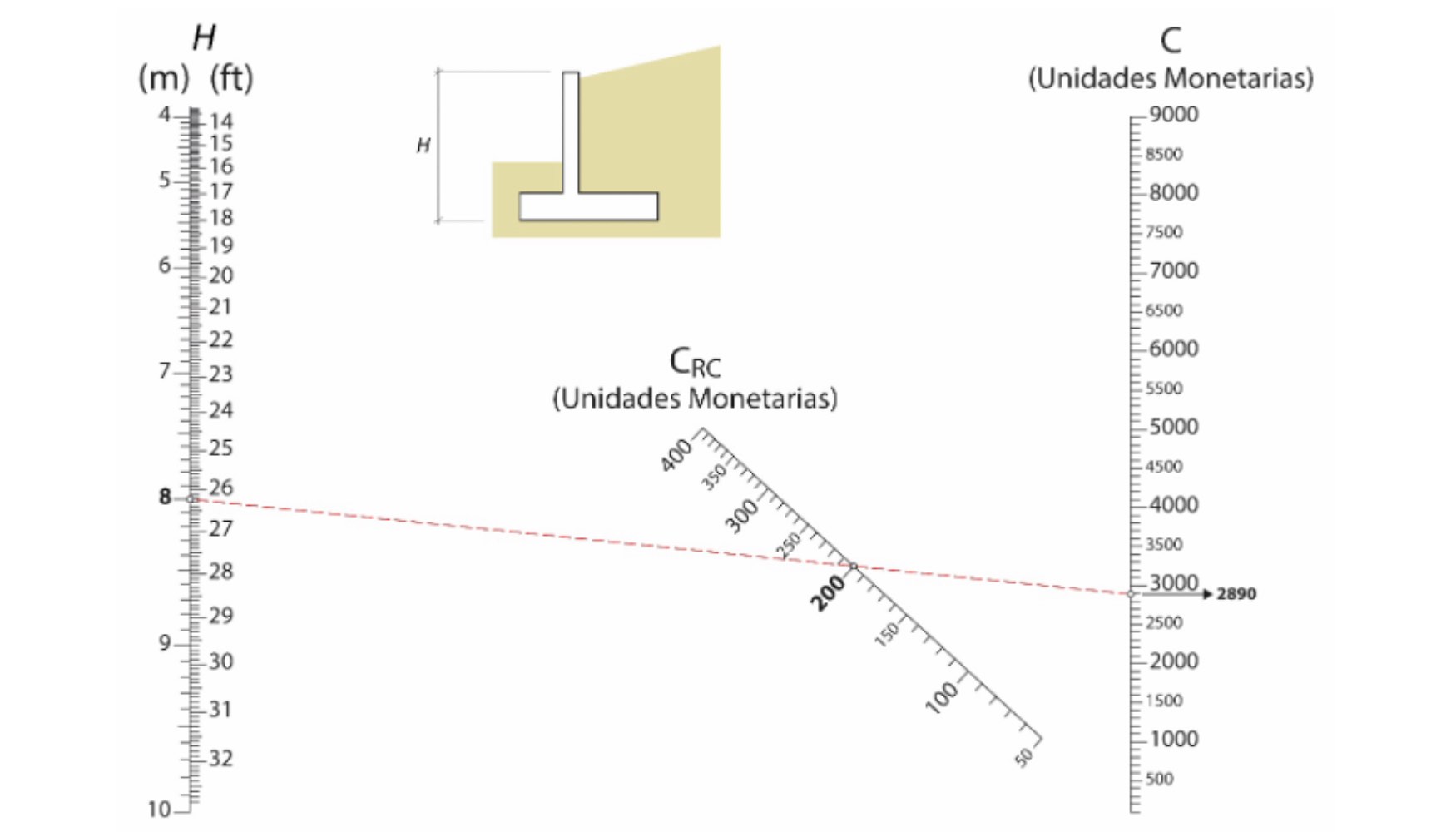
Por último, se incluye un nomograma que facilita la estimación del coste por metro lineal de un muro de contención de hormigón armado. Esta estimación no solo tiene en cuenta el coste del hormigón armado (CRC), sino también otros gastos adicionales, como los asociados a la forma de trabajo y diversos factores relacionados con la construcción y ejecución de la obra. Al integrar estos elementos, el cálculo obtenido ofrece una evaluación más precisa y completa de los requerimientos económicos del proyecto y proporciona a los proyectistas una herramienta útil para valorar su viabilidad.

El coste se expresa en unidades monetarias, en lugar de en una unidad monetaria específica, para garantizar su aplicación en diferentes contextos económicos y que la metodología siga siendo relevante a pesar de las variaciones regionales en los costes de materiales y mano de obra. El nomograma simplifica la estimación, ya que solo requiere dos variables de entrada: la altura total del muro (H, en metros) y el coste unitario de colocar el hormigón armado por metro cúbico. De este modo, los proyectistas pueden obtener una estimación del coste de forma rápida, sin necesidad de realizar cálculos complejos.

Es importante señalar que la expresión matemática y el correspondiente nomograma derivado de ella proporcionan solo una estimación aproximada. Por tanto, son una herramienta muy útil para realizar análisis preliminares de costes, pero no deben sustituirse por análisis de costes más exhaustivos durante la elaboración del presupuesto final de un proyecto de construcción. Será necesario realizar un estudio de costes más detallado cuando deban tenerse en cuenta variables específicas relacionadas con las características del emplazamiento, como las condiciones del suelo, los costes de transporte y los costes de mano de obra, con el fin de garantizar la exactitud de los resultados y su adecuación a las aplicaciones del mundo real.

Los resultados de este estudio contribuyen al avance de las metodologías de diseño preliminar de muros de contención de hormigón armado al relacionar de forma sistemática datos empíricos de optimización con diseños heurísticos tradicionales. En concreto, la elaboración de nomogramas basados en 63 diseños optimizados en términos de coste (Yepes et al., 2008) permite establecer una conexión directa y cuantificable entre los procedimientos computacionales modernos y las prácticas ingenieriles más tradicionales (MOPT, 1984; Calavera, 2001).

Los métodos tradicionales para diseñar muros en ménsula se basan generalmente en procesos iterativos de ensayo y error, en los que las decisiones finales dependen en gran medida de la experiencia del diseñador o ingeniero. Aunque estos procedimientos ofrecen soluciones estructuralmente adecuadas, no garantizan la eficiencia económica.

Los nomogramas propuestos en este trabajo superan estas limitaciones, ya que permiten obtener estimaciones rápidas con variables clave relacionadas con aspectos geométricos y de coste, validadas mediante modelos. De este modo, se presenta un método de optimización accesible (Carbonell et al., 2011; Penadés-Plà et al., 2018), que facilita su aplicación diaria por parte de los proyectistas.

La correspondencia entre los resultados del modelo y las reglas establecidas de forma empírica confirma la validez de la metodología propuesta. Por ejemplo, el hecho de que los espesores de la zapata y del alzado estén relacionados con la altura del muro en una décima parte de esta refleja su coherencia con las normas tradicionales (Calavera, 2001). No obstante, los modelos de regresión también ponen de manifiesto y cuantifican los efectos secundarios de los parámetros geotécnicos, como el peso específico del material de relleno y la capacidad portante del suelo. Estos factores tienden a descartarse en las primeras fases del diseño, por lo que los modelos mejoran los enfoques clásicos al adaptarse a los datos actuales.

Además, la evolución del cociente t/z en función de la altura del muro muestra una adaptación estructural que equilibra la seguridad con la eficiencia en el uso de materiales. Este comportamiento respalda las conclusiones previas de Yepes et al. (2008) sobre las ventajas económicas de la respuesta geométrica a las condiciones de carga y del terreno. Al integrar este comportamiento en un nomograma, se facilita su aplicación en las decisiones preliminares de diseño que, tradicionalmente, se han obviado en estas etapas.

El nomograma para la estimación de costes complementa este entorno de trabajo al traducir los parámetros estructurales en implicaciones monetarias. Al expresar los parámetros en unidades monetarias abstractas, se garantiza su flexibilidad en diferentes contextos económicos y su adaptación a las tendencias actuales en la planificación de infraestructuras en sus primeras etapas. A diferencia de los modelos puramente teóricos, este enfoque incorpora componentes prácticos de coste hasta la ejecución, lo que mejora su utilidad a la hora de tomar decisiones en el mundo real.

Por último, el programa PyNomo (Roschier, 2022) soluciona una limitación histórica en la construcción de nomogramas: su complejidad a la hora de realizarlos de forma manual (Adams, 1964). Esto ha despertado un renovado interés por la nomografía, respaldado por su relevancia técnica y didáctica (Doerfler, 2009), especialmente en el ámbito educativo (Martínez-Pagán y Roschier, 2022; Blight et al., 2025). De este modo, este estudio contribuye a la práctica ingenieril al preservar el cálculo tradicional, que tiene un gran potencial pedagógico.

A partir de los resultados obtenidos por Yepes et al. (2008), este trabajo presenta recomendaciones prácticas para el diseño de muros de contención de hormigón armado, que se han derivado de estudios previos de optimización. El objetivo de estas recomendaciones es mejorar la eficiencia estructural, reducir el coste de los materiales y facilitar la viabilidad constructiva. Al aplicar estas directrices durante el proceso de diseño, los proyectistas pueden desarrollar soluciones económicamente eficientes y funcionalmente óptimas para los muros de contención.

Las reglas para un diseño económico preliminar son las siguientes:

• La longitud de la zapata debe ser dos tercios de la altura total del muro.
• El espesor de la zapata y del alzado debe ser una décima parte de la altura total del muro.
• La longitud del talón debe ser una quinta parte de la altura total del muro más un metro.

Las reglas adicionales para el diseño aproximado de muros de contención de entre 4 y 10 metros de altura son las siguientes:

• La longitud de la zapata varía entre el 50% y el 60% de la altura total.
• La longitud del talón varía entre el 30% y el 40%, mientras que la longitud de la puntera podría llegar hasta el 20%.
• El espesor de la zapata y del alzado debería ser siempre del 10% de la altura total.

En cuanto a los requerimientos de material, el volumen de hormigón necesario se puede estimar como una sexta parte del valor del cuadrado de la altura total del muro, distribuido en una proporción de 3/2 entre el alzado y la zapata. Además, serán necesarios aproximadamente 60 kg de acero por metro cúbico de hormigón.

Este estudio presenta un conjunto de nomogramas diseñados para facilitar el proceso de diseño preliminar de muros de contención de hormigón armado y ofrece a los proyectistas una alternativa eficiente y fiable frente a los métodos tradicionales de prueba y error. Basados en datos de 63 diseños optimizados, estos gráficos permiten estimar rápidamente los parámetros geométricos clave y su coste, lo que agiliza la toma de decisiones en las primeras etapas del diseño. La incorporación de estos nomogramas en la práctica ingenieril fomenta un enfoque más sistemático y objetivo, y reduce la dependencia de suposiciones empíricas y de la experiencia individual.

Los resultados muestran que la altura total del muro es el factor principal que determina sus dimensiones. La longitud del pie suele situarse entre el 50% y el 60% de la altura, mientras que el espesor del alzado y de la zapata varía entre el 7% y el 18%. Además, conforme aumenta la altura del muro, la proporción de la zapata destinada al talón disminuye, mientras que la correspondiente a la puntera aumenta para resistir mejor las presiones del terreno. Esta tendencia respalda la solidez de la metodología propuesta, en concordancia con los principios estructurales establecidos.

Más allá de la estimación geométrica, el estudio destaca la importancia de los nomogramas para optimizar los costes. La herramienta de estimación permite evaluar de manera práctica los gastos de material y comparar distintas alternativas de diseño sin necesidad de realizar cálculos extensos y laboriosos. También se ofrecen recomendaciones clave para un diseño económico, entre las que se destaca que la longitud del pie debe ser aproximadamente dos tercios de la altura total del muro. También facilita la estimación del consumo de material con indicaciones sencillas y fiables.

En particular, los nomogramas propuestos constituyen un conjunto de herramientas intuitivas y prácticas para los proyectistas, ya que promueven un enfoque más estructurado y eficiente para la reducción de costes en muros de contención. Estas herramientas simplifican el diseño preliminar sin sacrificar la precisión, la seguridad estructural, la eficiencia en el uso de materiales ni la viabilidad económica, y facilitan una toma de decisiones más informada.

Referencias

Adams, D. P. (1964). Nomography: Theory and application. Archon Books.

Blight, T., Martínez-Pagán, P., Roschier, L., Boulet, D., Yepes-Bellver, L., & Yepes, V. (2025). Innovative approach of nomography application into an engineering educational context. PLOS ONE, 20(2), e0315426. https://doi.org/10.1371/journal.pone.0315426

Boulet, D., Doerfler, R., Marasco, J., & Roschier, L. (2021). What Can PyNomo Do for Me? Retrieved March 18, 2025, from http://lefakkomies.github.io/pynomodoc/introduction/introduction.html

Calavera, J. (2001). Muros de contención y muros de sótano. Madrid: Intemac.

Carbonell, A., González-Vidosa, F., & Yepes, V. (2011). Design of reinforced concrete road vaults by heuristic optimization. Advances in Engineering Software, 42(4), 151–159. https://doi.org/10.1016/j.advengsoft.2011.01.002

Doerfler, R. (2009). Creating nomograms with the PyNomo software. Retrieved March 18, 2025, from https://deadreckonings.com/2009/07/31/creating-nomograms-with-the-pynomo-software/

Douglas, J., & Danciu, L. (2020). Nomogram to help explain probabilistic seismic hazard. Journal of Seismology, 24(1), 221–228. https://doi.org/10.1007/s10950-019-09891-2

Glasser, L., & Doerfler, R. (2019). A brief introduction to nomography: Graphical representation of mathematical relationships. International Journal of Mathematical Education in Science and Technology, 50(8), 1273–1284. https://doi.org/10.1080/0020739X.2019.1656827

Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680. https://doi.org/10.1126/science.220.4598.671

Martínez-Pagán, P., & Roschier, L. (2022). Nomography: A renewed pedagogical tool for science and engineering higher education studies. Heliyon, 8(6), e09731. https://doi.org/10.1016/j.heliyon.2022.e09731

Martínez-Pagán, P., Yepes, V., Roschier, L., Boulet, D., & Blight, T. (2023). Introducción de los códigos abiertos Pynomo y Nomogen para la elaboración de nomogramas en el ámbito de la ingeniería civil y minería. Ingeopres, 302, 54-58.

Ministerio de Obras Públicas y Transportes. (1984). Norma Tecnológica de la Edificación NTE A+C: Acondicionamiento del terreno. Cimentaciones. Madrid.

Mottola, G., & Cocconcelli, M. (2023). Nomograms in the history and education of machine mechanics. Foundations of Science. https://doi.org/10.1007/s10699-022-09890-w

Penadés-Plà, V., García-Segura, T., Martí, J. V., & Yepes, V. (2018). An optimization-LCA of a prestressed concrete precast bridge. Sustainability, 10(3), 685. https://doi.org/10.3390/su10030685

Roschier, L. (2022). PyNomo 0.3.2. Retrieved from http://lefakkomies.github.io/pynomo-doc/installation/installation.html (Accessed 18 March 2025).

Yepes, V., Alcalá, J., Perea, C., & González-Vidosa, F. (2008). A parametric study of optimum earth retaining walls by simulated annealing. Engineering Structures, 30(3), 821–830. https://doi.org/10.1016/j.engstruct.2007.05.023

Yepes, V., González-Vidosa, F., Alcalá, J., & Villalba, P. (2012). CO2-Optimization Design of Reinforced Concrete Retaining Walls based on a VNS-Threshold Acceptance Strategy. Journal of Computing in Civil Engineering, 26 (3):378-386. https://doi.org/10.1061/(ASCE)CP.1943-5487.0000140

Yepes-Bellver, L., Brun-Izquierdo, A., Alcalá, J., & Yepes, V. (2025). Surrogate-assisted cost optimization for post-tensioned concrete slab bridges. Infrastructures, 10(2), 43. https://doi.org/10.3390/infrastructures10020043