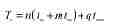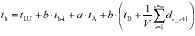Obtención automática de las secuencias de plegado de la chapa

Este artículo presenta un método para resolver el problema de la secuencia de plegado en la fabricación de piezas de chapa. El algoritmo desarrollado descompone la pieza en formas básicas (canales y espirales) y obtiene las secuencias parciales asociadas a cada una de ellas. Combinando estas secuencias parciales se obtienen las secuencias completas asociadas a la pieza completa. Para hacer esta combinación de secuencias y reducir el número de posibles soluciones, se establecieron diversas estrategias. Las secuencias (parciales y completas) son chequeadas desde el punto de vista de posibles colisiones con la herramienta y de las restricciones impuestas por las tolerancias. En la última etapa se ordenan las secuencias teniendo en cuenta el tiempo total de proceso de cada una de ellas y la secuencia asociada al menor tiempo se selecciona como solución óptima.

Palabras clave: chapa, plegado, secuencias de plegado, CAPP

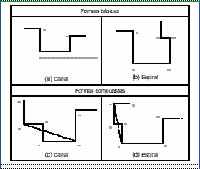
Figura 1. Formas básicas y compuestas

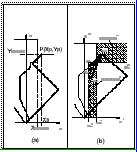
Figura 2. Análisis de colisiones

Tener en cuenta todos los factores (colisiones, tolerancias, tiempos de plegado, etc.) que influyen a la hora de seleccionar las secuencias válidas de plegado de una chapa es algo complejo, pero aún lo es más si se tiene en cuenta el número elevado de posibles secuencias (n!2n) que deberían ser analizadas con el fin de comprobar su validez. Por esta razón, y con el fin de reducir el número de secuencias a analizar, se deben establecer estrategias y reglas de tipo heurístico que permitan rápidamente la búsqueda de aquellas secuencias válidas [2, 4]. Algunas investigaciones han tenido en cuenta las restricciones impuestas por las tolerancias [1], mientras que otras se han centrado más en aspectos económicos y en el análisis de los tiempos de plegado [3, 5].

En este trabajo, se propone un sistema para la obtención de secuencias en piezas de chapa con pliegues paralelos, teniendo en cuenta los tres aspectos de influencia citados. El método desarrollado, se basa en dividir la pieza en formas básicas y compuestas de tipo canal (dos pliegues consecutivos sobre la misma cara) o espiral (tres pliegues consecutivos sobre la misma cara) (Figura 1). Los canales y espirales compuestos son aquellos que contienen, a su vez, uno o más canales básicos (Figura 1c y 1d).

La ventaja de este método consiste en que para eliminar una secuencia completa de plegado de la pieza, basta con haber eliminado previamente alguna secuencia parcial de pliegues asociada a una de sus formas básicas. Si a esto se añaden las estrategias definidas para ensamblar entre sí las secuencias parciales de la pieza, se reducirá sustancialmente el tiempo de búsqueda de las secuencias de plegado completas.

Tras descomponer la pieza en formas básicas y compuestas, se procede a la construcción de un árbol que muestra las relaciones jerárquicas existentes entre ellas. Para ello, basta con saber que una forma básica está relacionada con una compuesta cuando uno de sus pliegues principales coincide. Así, el árbol tendrá tantos niveles como relaciones de ascendencia entre formas básicas y compuestas existan (Figura 6).

Forma básica Posible colisión Restricciones para evitar colisión

Canal B * A

Espiral C * (A, B)

La posible colisión con el punzón se detecta comprobando si las coordenadas de cada uno de los nodos (pliegues ya realizados o no) de la chapa se encuentra a uno u otro lado de las fronteras que definen la geometría del punzón. En algunos casos, este cálculo no es suficiente. Por ejemplo, en el caso mostrado en la Figura 2a, el nodo P de coordenadas (XP, YP) está fuera del contorno del punzón y sin embargo existe colisión. Para encontrar este tipo de choques se divide el entorno del punzón en una serie de regiones y se lleva a cabo el estudio de varios casos particulares en función de la región en la que se encuentre cada nodo analizado y sus nodos contiguos. A modo de ejemplo, en el caso mostrado en la Figura 2b, el nodo P que se está estudiando puede estar en una cualquiera de las tres posiciones (P1, P2 ó P3) de la Zona_2+ y el anterior a él (P0) en la Zona_1+, lo que puede motivar un choque a la altura de la coordenada Y6+. Para comprobarlo se calcula el valor de la coordenada X para un punto (X, Y6+) sobre la recta que une los puntos P0 y P (P1, P2 ó P3) y se compara con X6+. Si, X(Y6+) > X6+ se producirá choque y P _ P2 ó P _ P3. Si por el contrario, X(Y6+) > X6+ entonces no habrá choque y P _ P1.

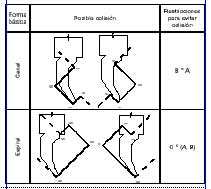
Figura 3. Ejemplo de restricciones de orden impuestas para evitar colisiones (*:antes que)

En la Figura 3 se muestran dos ejemplos de las restricciones impuestas a canales y espirales con el fin de evitar posibles colisiones herramienta-pieza. A modo de ejemplo, en la Figura 6 se muestran las secuencias parciales libres de colisión asociadas a las forma básicas y compuestas de la pieza usada como ejemplo.

Como criterio para encontrar rápidamente una primera secuencia de plegado, se establece en primer lugar el orden de unión entre las formas básicas o compuestas de un mismo nivel. Para ello, se tiene en cuenta la Profundidad de cada forma en el mismo nivel. Los pliegues con mayor Profundidad son los más alejados del centro de la pieza y el criterio establece que estos deben realizarse en primer lugar. Para el nivel_1 de la pieza representada en la Figura 6, la profundidad media de la espiral es mayor que la del canal y por tanto las secuencias de pliegues correspondiente al nivel_1 de este ejemplo, estarán formadas por las secuencias de los pliegues asociados a la espiral, seguidas por las secuencias asociadas a los pliegues del canal compuesto (ver Figura 6).

A continuación se añaden el resto de secuencias correspondientes a niveles inferiores. Esta última operación se realiza teniendo en cuenta que las formas de unos y otros niveles están ligadas por un nodo común utilizado anteriormente en la construcción de la estructura de árbol. La cifra de secuencias obtenida (240) se puede reducir modificado el orden de prioridad entre las secuencias parciales correspondientes al canal básico del nivel_2 con el fin de el fin de eliminar más rápidamente las posibles secuencias completas que originan colisión.

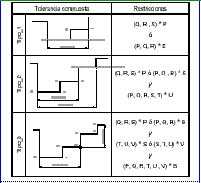
Figura 4. Restricciones debidas a las tolerancias su proceso de plegado

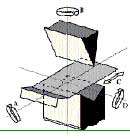
Figura 5. Direcciones de manipulación de la pieza durante el proceso de plegado

Las tolerancias que pueden afectar a la secuencia de plegado son aquellas denominadas compuestas, que afectan a más de dos pliegues consecutivos [4]. En la Figura 4 se muestran las restricciones impuestas para obtener las secuencias de plegado compatibles con cada tipo de tolerancia compuesta considerada. Estas tolerancias pueden afectar a pliegues de alguna forma básica (canal o espiral) de la pieza o a pliegues contenidos en dos formas básicas, lo que obliga a analizar, desde el punto de vista de las tolerancias, tanto las secuencias parciales (asociadas a formas básicas) como las completas (asociadas a la pieza completa). La Figura 6 muestra la aplicación de las restricciones impuestas por las tolerancias compuestas sobre la pieza ejemplo, así como las secuencias válidas obtenidas.

Para calcular el tiempo total de plegado se empleará la expresión siguiente [4]:

(1)

donde, n es el tamaño del lote a fabricar, tb es el tiempo de plegado de cada pieza, tB es el tiempo en realizar un giro de tipo B, m es el número de veces que se cambia la zona de sujeción, tSU es el tiempo de montaje y ajuste de las parejas punzón-matriz y q el número de parejas punzón-matriz utilizadas. El tiempo de plegado se calcula mediante la expresión (Figura 5):

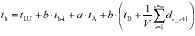
(2)

donde b es el número de pliegues de cada secuencia completa, a es el número de giros de tipo A necesarios para realizar todos los pliegues de la misma y tA y tD son respectivamente los tiempos empleados en realizar cada giro de tipo A y D, tb-i es el tiempo empleado en el ascenso y descenso del punzón para cada pliegue i, tLU es el tiempo de carga y descarga de la pieza y di_i+1 representa la distancia, medida en la dirección C entre dos pliegues de una misma secuencia situados en el orden i e i+1.

En la Figura 6 se incluye el tiempo de plegado para todas las secuencias válidas correspondiente a la pieza ejemplo, considerando como datos: n = 1, q = 1, tb-i = 5s, tA = tC = 1s, tB = 15s, tSU = 120s, tLU = 6s, V = 300 mm/s. El tiempo mínimo obtenido es de 241,5s, y se corresponde con la secuencia: 7-6-5-4-8-2-3.

El sistema descrito permite gran rapidez en la obtención de soluciones válidas, sin necesidad de realizar el análisis de cada una de las secuencias teóricas de plegado. Otra ventaja importante del sistema desarrollado es que permite al usuario fijar la búsqueda de secuencias válidas en base a una o más restricciones, independientemente. Así por ejemplo, se pueden obtener las secuencias válidas desde el punto de vista exclusivo de las colisiones o de las tolerancias o teniendo en cuenta ambas restricciones conjuntamente. En cualquier caso se pueden ordenar las secuencias obtenidas en base al tiempos total de plegado.

1. de Vin, L.J., de Vries, J. y Streppel, T., Process planning for small batch manufacturing of sheet metal parts. Int. J. Prod. Res., 38 (17) (2000) pp. 4273-4283.

2. Duflou, J.R., van Oudheusden, D., Kruth, J.-P. y Cattrysse, D., , Methods for the sequencing of sheet metal bending operations. Int. J. Prod. Res., 37 (14) (1999) pp. 3185-3202.

3. Gupta, S.K., Bourne, D.A., Kim, K.H. y Krishnan, S.S., Automated Process Planning for sheet metal bending operations. J. Mfg. Systems, 17 (5) (1998) pp. 338- 360.

4. Shpitalni, M. y Radin, B., Critical Tolerance Oriented Process Planning in Sheet Metal Bending. Journal of Mechanical Design, 121 (1999) pp. 136-144.

5. Wang, CH.-H. y Bourne, D.A., Design and manufacturing of sheet-metal parts using features to aid process planning and resolve manufacturability problems. Robotics & Computer Integrated Manufacturing, 13 (3) (1997) pp. 281-294.

Este artículo es resultado de la investigación realizada en el Proyecto FEDER (Ref. 1FD97-0677) cuyo objetivo se centraba en el desarrollo de un sistema de planificación para el punzonado y plegado de la chapa

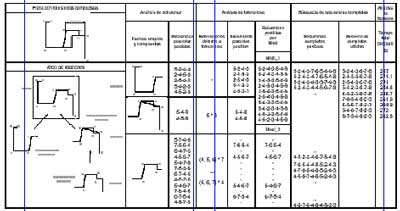
Figura 6. Ejemplo de secuencias parciales y completas válidas (según colisiones, tolerancias y tiempo de plegado) para una pieza ejemplo