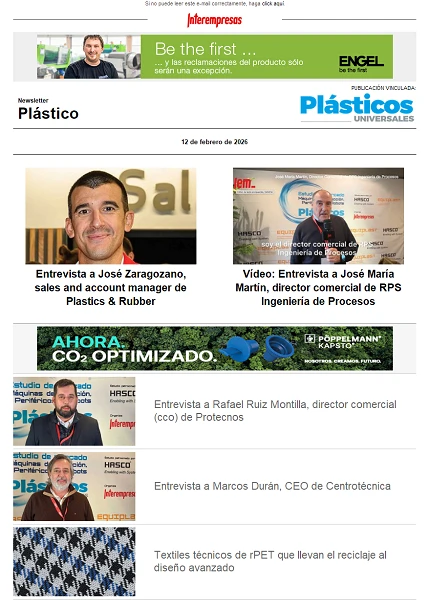
Simulación del proceso de inyección en el diseño de piezas de plástico

Introducción

El diseño de una pieza o artículo de plástico es un proceso de gran complejidad en el que el diseñador, además de conocer los requerimientos funcionales de la pieza, debe conocer y estar familiarizado con las propiedades de los materiales plásticos, el proceso de transformación, así como las condiciones a que estará sometida la pieza durante su vida en servicio.

En el lanzamiento al mercado de un nuevo producto, deben seguirse una serie de etapas, todas ellas interrelacionadas. Esto incluye básicamente todos los pasos esenciales en la vía de obtener piezas de gran calidad [1] como diseño de la pieza, diseño del molde, mecanizado del molde e inyección de las piezas.

A medida de que las piezas inyectadas han ido ganando más y más campo en el ámbito de la ingeniería ha ido creciendo la necesidad de incrementar la calidad de los productos transformados. Todo ello hace que los requisitos que se piden a las piezas y al proceso de inyección sean cada vez más exigentes.

La distribución del material dentro del molde, así como las orientaciones de flujo, y los diferentes grados de contracción que pueden producirse deben calcularse, y en su caso estimarse antes de la construcción del molde.

De todo ello se deriva la complejidad del diseño y el completo conocimiento del proyecto que debe tener el diseñador, pues cada cambio producido puede afectar y condicionar a todos los demás, sufriendo así el proyecto diversas iteraciones y replanteamientos en las diferentes etapas, lo que requiere un cierto grado de experiencia, así como el empleo de criterios conservadores en las estimaciones efectuadas, antes de proceder a la construcción del molde, determinar la fiabilidad de la pieza transformada y pasar al proceso de fabricación en serie.

Simulación del proceso de inyección

El desarrollo de métodos de cálculo numérico por ordenador y la aparición de ordenadores cada vez más potentes, está permitiendo la implementación cada vez más extensiva de técnicas CAD/CAE para el cálculo y diseño de piezas de plástico. Comercialmente existen diversos paquetes informáticos para el diseño de moldes y control del proceso de inyección [2] que proporcionan al ingeniero nuevas herramientas para el diseño. La utilización de la simulación numérica reduce la probabilidad de cometer errores y disminuye costes en la fabricación, en el proceso de fabricación, y en la no calidad del producto final.

Una de las más importantes técnicas de simulación numérica es el método de los elementos finitos/diferencias finitas, tal como comentamos en artículos anteriores [3]. Cabe recalcar el hecho de la importancia de una correcta modelización de la geometría y discretización del molde [4], de la caracterización de los materiales (polímero, molde y refrigerante), parámetros de proceso, ecuaciones aproximadas que gobiernan los campos de temperatura, flujo y presiones del sistema, y de los diferentes algoritmos de cálculo [5-6].

A título de ilustrar esta exposición, se acompañan los principales resultados del análisis mediante el programa C-Mold de A.C.Technology [7] de un molde del cuerpo de una bomba periférica. Dichos resultados permiten establecer los parámetros óptimos de transformación, así como prever cuantitativamente la contracción y deformación final de la pieza.

Todos los programas de simulación del proceso de inyección tienen la misma estructura interna (Figura 1):

Figura 1 Estructura modular del C-mold

- Un preprocesador para la modelización de la geometría de manera que sea inteligible por el ordenador.

- Unas bases de datos que almacenan características necesarias para el cálculo. Así es necesaria una constante actualización de la base de datos de polímeros comerciales, refrigerantes, materiales del molde y de características de las máquinas de inyectar existentes en el mercado.

- Una serie de módulos de cálculo específicos para cada proceso de transformación. Es usual en estos programas disponer de una plantilla para agilizar el proceso de preparar los parámetros necesarios para el cálculo.

- Un postprocesador que presenta los resultados del análisis de una manera fácil de interpretar por el usuario.

El modelo geométrico se ha realizado partiendo de una geometría sencilla importada desde un programa de CAD. Dicha geometría básica ha sido con posterioridad modificada convenientemente a través del preprocesador del programa para una correcta modelización y discretización del molde, incluyendo coladas de alimentación y circuitos de atemperación (Figura 2). Los espesores de la carcasa de la bomba varían desde los 1.6 mm de los diferentes nervios laterales a los 11 mm de la zona próxima al rodete.

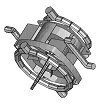Figura 2 Geometría del cuerpo de una bomba periférica

La baja conductividad térmica, junto con las contracciones que sufre el material plástico al enfriarse dentro del molde condicionan el espesor máximo que puede tener la pieza inyectada, obligando a diseñar con grandes superficies específicas, a fin de evitar vacuolas internas o los rechupes superficiales que puedan producirse al enfriarse la acumulación de material producida. Esta característica y la poca potencia de cálculo que tenían antiguamente los ordenadores hace que todos los programas comerciales de simulación del proceso de inyección modelicen la geometría de las piezas a través del mallado de superficies y no trabajen con elementos tridimensionales..

Los diferentes parámetros para la caracterización del polímero utilizado (Hostacom GUO1, polipropileno cargado con un 30% de fibra de vidrio) fueron suministrados por Hoechst. Estos parámetros comprenden calor específico, conductividad térmica, densidad, temperatura de transición, curvas de viscosidad, curvas PVT, tensor isoelástico y coeficiente de expansión isotérmica.

Una vez analizados los requerimientos de funcionamiento de la bomba en servicio, un estudio de la simulación reológica del llenado del molde permite optimizar el proceso de inyección y mejorar la calidad final de la pieza.

Según el nivel de análisis se pueden distinguir tres tipos de soluciones dentro del proceso de simulación de la inyección de termoplásticos: una solución de proceso, una solución de productividad y una solución de calidad.

Solución de proceso

La solución de proceso, fruto exclusivamente del estudio del llenado del molde, permite: conocer el número y disposición de las entradas; la obtención de un sistema bien balanceado; determinar el perfil de velocidades de inyección óptimo para minimizar las tensiones residuales [8]; encontrar el tiempo de llenado más adecuado; evaluar la posición y calidad de las líneas de soldadura y atrapamientos de aire; determinación de la orientación de las fibras; y estimar la presión de inyección. Así esta solución permite diseñar en una primera fase la cavidad del molde, el sistema de llenado y evacuación de gases, así como dimensionar en una primera etapa las características de la máquina de inyectar necesaria.

Para establecer los parámetros óptimos de transformación hay que establecer lo que se conoce como un a ventana de proceso, que consiste en fijar los parámetros de transformación lo más centrados posible en el margen de tolerancia propio de cada uno de ellos, de forma que se pueda aceptar unos márgenes amplios de variabilidad del proceso, manteniendo costes y calidad de fabricación dentro de las especificaciones. Además de estas consideraciones hay que optimizar el proceso, tendiendo a minimizar el tiempo de ciclo y energía gastada en la transformación.

Uno de los criterios de determinación de tiempo óptimo es el de la mínima presión de inyección, siempre que la diferencia de temperatura entre las zonas más calientes y más frías de la pieza no sean excesivas. Asimismo hay que asegurarse que todos los parámetros están dentro de las especificaciones.

Algunas de las principales conclusiones obtenidas del análisis del llenado de la cavidad del molde en nuestro caso son:

- En el gráfico de la Figura 3 se muestra la evolución del llenado del molde desde los primeros instantes de la inyección (colores fríos) hasta el final del llenado (colores cálidos). Aunque la distancia entre isocronas no sea del todo constante y el final del llenado no se produce al mismo instante a ambos lados de la pieza, el flujo del material plástico puede considerarse relativamente bien balanceado, lo que favorece la estabilidad dimensional.

Figura 3 Frente de llenado del molde

- La situación de las líneas de soldadura no reviste especial importancia para la resistencia de la pieza ya que los espesores son muy elevados y las temperaturas en la unión de los dos frentes es suficientemente elevada.

- Todas las oclusiones de aire se presentan en el plano de partición del molde o de las correderas.

Solución de troductividad

La solución de productividad permite: evaluar la eficacia en la evacuación de los diversos circuitos de refrigeración; establecer el caudal y temperaturas del refrigerante; evitar la existencia de puntos calientes; conocer la distribución de temperaturas; estimar el tiempo de consolidación de la entrada; y la determinación del tiempo de ciclo mínimo.

El análisis del atemperado del molde es un factor de gran importancia en la rentabilidad y calidad de la pieza transformada, en especial si se utilizan materiales semicristalinos. Desde el punto de vista de la productividad el análisis de la productividad del molde puede proporcionar dos tipos de datos muy importantes para el diseño del molde:

Uno de ellos es el gráfico de diferencias de temperatura entre las paredes del molde y el centro de la pieza (Figura 4), promediado a lo largo de todo el ciclo.

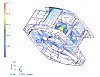Figura 4 Diferencia de temperaturas entre el centro y la superficie

Cualitativamente representa el potencial de deformación o alabeo debido a la refrigeración no balanceada. En el caso que estamos analizando estas diferencias son muy acusadas -más de 40C- por la insuficiente refrigeración en la zona interior de la carcasa de la bomba periférica, por lo que ocasionará un enfriamiento asimétrico contribuyendo a la generación de tensiones residuales.

Esta deficiencia en la refrigeración es difícil de solucionar por la propia geometría de la pieza y por la forma y disposición de las correderas del molde.

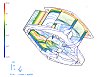Figura 5 Mapa de temperatura en el molde

Otro gráfico de interés es el tiempo que necesita cada punto en enfriarse hasta la temperatura de expulsión especificada (Figura 5). A partir de este mapa se identifican claramente las zonas que necesitan mucho más tiempo que otras para enfriar y que hacen aumentar el tiempo de ciclo total.

Solución de calidad

La solución de calidad, además de las características de la solución de productividad, permite evaluar: el aspecto externo, el cumplimiento de tolerancias, la existencia de rechupados, contracciones y deformaciones (alabeos); la visibilidad de las líneas de soldadura; la predicción de tensiones residuales y conocer el perfil óptimo de presión de mantenimiento.

La magnitud y duración de la presión de mantenimiento es de gran importancia para la estabilidad dimensional y calidad de la pieza. El criterio para establecer dicho perfil será el evitar reflujos de material y minimizar la contracción volumétrica [9-10].

Para minimizar la contracción volumétrica se debe buscar un equilibrio entre el tiempo de mantenimiento de presión y el perfil de presión posterior. Con el tiempo de mantenimiento escogido no se observa reflujo de material. Sin embargo la contracción volumétrica es realmente elevada a causa de los elevados espesores (11 mm) en la zona más alejada del punto de inyección, mientras que en zonas cercanas varía entre 1.6 y 6 mm (Figura 6). Todo ello hace que se solidifique la entrada de material mucho antes que el resto de la pieza con lo que no se puede suministrar más material que contrarreste la contracción al enfriarse la pieza en la cavidad del molde.

Figura 6 Contracción volumétrica

La deformación total de la pieza es debida casi exclusivamente a deficiencias en la compactación de la misma y no por una refrigeración mal balanceada (Figura 7). No obstante, estos valores son muy inferiores al milímetro de diferencia, por lo que se puede asegurar la estanqueidad de la bomba en funcionamiento.

Figura 7 Deformación axial del cuerpo de la bomba

Conclusiones

Inevitablemente, el desarrollo tecnológico de nuestra sociedad exige la aplicación de programas de simulación de llenado de moldes, especialmente en el caso de piezas de plástico de geometría complicada cuya realización práctica con los métodos tradicionales sería casi imposible de seguir. De todo ello segura una mejora en la calidad de vida, un avance tecnológico, y una ventaja competitiva.