Caracterización de un robot para aplicaciones de mecanizado con requerimientos de tolerancias
Hasta la fecha, los robots industriales se aplican a rebarbados sin requerimientos de tolerancias, en las 2 variantes posibles; robot coge pieza / robot coge herramienta; mecanizado con requerimientos de tolerancias poco exigentes, de tipo desbaste; y mecanizado con exigencias de tolerancias para dedicación exclusiva a operaciones de mecanizado, siendo en la práctica un CNC.
Motivado por este potencial, el presente artículo analiza la caracterización preliminar del comportamiento de un robot en un entorno dinámico típico de mecanizado. Se pretende entender cómo se comporta este tipo de recurso para conocer qué habría que añadirle para su participación en operaciones de mecanizado con requerimientos de tolerancias en apoyo a los CNCs.
La arquitectura de robot seleccionada es de tipo Scara. La búsqueda de un robot cómodo de modelar y de analizar cinemática y dinámicamente, sin limitaciones relevantes en la multifuncionalidad de trabajos solicitados, ha llevado a esta elección inicial, frente a la arquitectura objetivo de los robots antropomórficos de 6 grados de libertad, tan extendidos a nivel industrial.
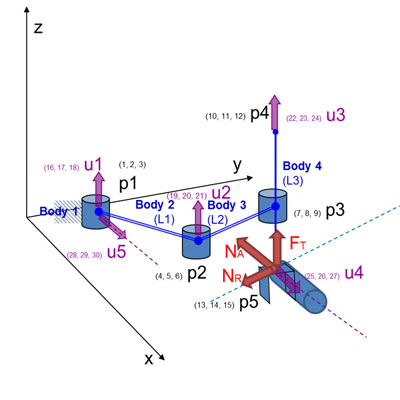
Dispone de 3 uniones, de las cuales 2 son de tipo par de revolución (1 grado de libertad cada una) y la tercera es de tipo corredera o par cilíndrico (2 grados de libertad). La primera unión, de tipo par de revolución, sirve para unir el suelo (considerado como eslabón número 0) con el eslabón número 1. La segunda unión, también de ese tipo, une el eslabón número 1 con el eslabón número 2. Estos 2 brazos pueden describir un movimiento horizontal en el plano x-y. El tercer eslabón está unido al eslabón número 2 por la unión de tipo corredera. El movimiento que puede describir es paralelo al eje z. El robot es de 4 grados de libertad (4 motores).
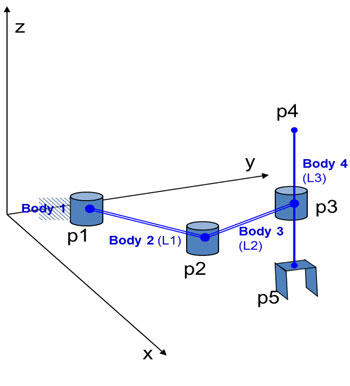

En relación a los posibles trabajos que puede realizar este tipo de robot, su versatilidad abarca tanto operaciones típicas de manipulación (funcionalidad inicial) como operaciones de arranque de viruta (nueva funcionalidad añadida).
Uno de los mecanizados más usuales es el taladrado, por lo cual se elige éste para su modelización y análisis. Dentro del taladrado se elegirá para acotar las fuerzas, taladrado en macizo con broca de diámetro 9 mm.
Se ha considerado para este estudio que el robot tenga comportamiento de sólido rígido, al ser el mayor efecto esperado el de los pares en las uniones.
Para modelarlo se utiliza el método de los sistemas multicuerpo. Dentro de este método existen diversos tipos de formulaciones, p.e. Denavit-Hartenberg (D-H). D-H genera una cantidad muy elevada de ecuaciones e incógnitas. Esas incógnitas son de difícil comprensión y, para cada posición, es preciso detenerse a interpretar qué significado físico tienen.
Se ha optado por la formulación de coordenadas naturales. Este sistema utiliza puntos y vectores unitarios para definir la posición de los distintos cuerpos, y permite compartirlos cuando es posible y se quiere para definir los pares cinemáticos y reducir al mismo tiempo el número de variables. Las incógnitas son intuitivas, las ecuaciones de restricción muy sencillas y se reduce considerablemente el número de ecuaciones e incógnitas.
Sin embargo, las coordenadas naturales ‘puras’ tienen 2 problemas. El primero, que 2 elementos con un ángulo de 0 ó 180 grados dan lugar a puntos singulares que pueden crear problemas en las ecuaciones de restricción y por lo tanto han de evitarse. El segundo, que tampoco inciden directamente sobre la definición o el origen de los movimientos. Por lo tanto, es muy conveniente complementar esta formulación con ángulos y distancias (coordenadas relativas). Esto da lugar a las coordenadas naturales mixtas, que es la formulación final elegida.
Las coordenadas naturales mixtas no tienen el problema de los puntos singulares. La ventaja más significativa reside en su utilidad a la hora de aplicar fuerzas motrices, momentos o evaluar errores. Al incidir sobre la incógnita origen (ángulos o distancias) controla los motores de manera directa.
El algoritmo, la simulación y la obtención de resultados se ha programado mediante Matlab.
Para realizar el modelo en coordenadas naturales mixtas, es preciso modelar en 2 pasos el robot a estudio; designados por modelo 1 y modelo 2.
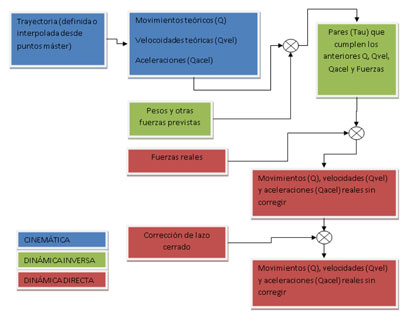
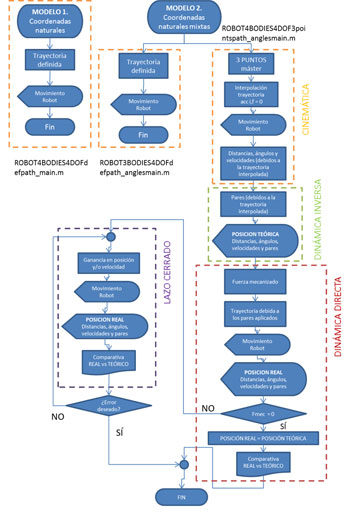
Modelo 1
El primer modelo se basa en coordenadas naturales. Para su validación, se plantea una trayectoria definida y se analiza cinemáticamente si el robot satisface el movimiento solicitado, manteniendo su integridad como sistema multicuerpo.
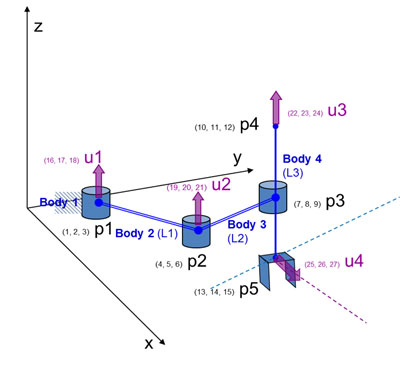
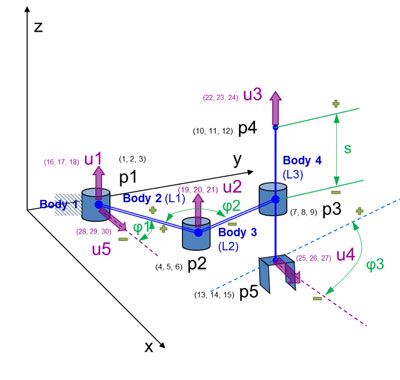
Se cuantifican los puntos (en este caso inicial y final) que configuran el robot. Al tratarse de sólidos rígidos, cada eslabón queda definido por sus respectivos puntos inicial y final (que son los más interesantes para la cinemática y la dinámica) y por un vector unitario no colineal a esos 2 puntos. Los vectores unitarios se colocan en los lugares en los que se tenga un eje de rotación o cuando se desee obtener información de un ángulo. No son necesarios vectores unitarios para medir distancias. Tampoco tienen por qué coincidir los grados de libertad con el número de vectores unitarios.
Las longitudes de cada eslabón quedan definidas como constantes geométricas. Se establecen las restricciones que definen la naturaleza del robot y las relaciones entre los diferentes elementos y su entorno.
La trayectoria se genera por una nube de puntos continua, definidos en coordenadas independientes.
Cada conjunto de coordenadas independientes define en un instante concreto, una posición y postura de robot determinada. Para conocerla, es necesario saber qué coordenadas dependientes hay en ese instante. Las coordenadas se obtienen al resolver, por el método de Newton-Rhapson, las ecuaciones de restricción en función de las coordenadas independientes. El motivo de hacerlo así es porque las coordenadas dependientes deben satisfacer las restricciones, cosa que no ocurre con las coordenadas independientes.
Una vez probado el modelo (primera validación), se pasa al modelo 2.
Modelo 2, con análisis cinemático con trayectorias definidas
El modelo 2 incorpora a las coordenadas naturales del modelo 1 las coordenadas relativas en forma de ángulos en los pares de revolución (3 ángulos; ϕ1, ϕ 2 y ϕ3) y distancias en los pares prismáticos (1 distancia; s). Estas coordenadas relativas pasan a ser las nuevas coordenadas independientes (sustituyendo a las coordenadas independientes cartesianas del modelo 1, que eran coordenadas naturales).
Es necesario revisar si el sistema de vectores unitarios del modelo 1 es suficiente o no. Para este caso concreto, se ha necesitado añadir 1 vector unitario adicional con objeto de que los ángulos queden perfectamente determinados con las correspondientes ecuaciones de producto escalar y/o vectorial.
Las restricciones habrán de ser incrementadas en, al menos, 4 ecuaciones, una por cada nueva incógnita.
La validación del modelo 2, se hace en 2 etapas. La primera, al igual que se hizo en el modelo 1, a través del análisis cinemático del comportamiento con una trayectoria definida. Podrían obtenerse del modelo 2 en este análisis, velocidades y aceleraciones, pero no son necesarias. Tan sólo interesan los movimientos o desplazamientos finitos.
Comprobada la coherencia de movimientos (segunda validación), se pasa a analizar cinemáticamente el comportamiento con trayectorias interpoladas.
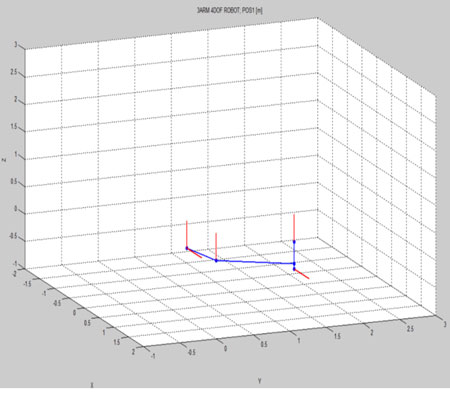
Modelo 2, con análisis cinemático con trayectorias interpoladas
El análisis cinemático con trayectorias interpoladas, trabaja con un número mínimo de 3 puntos máster. En este caso se han elegido 3; punto inicial, punto intermedio y punto final. El número de interpolaciones con el que se actúa es de 50 interpolaciones en cada tramo (cada 2 puntos máster hay un tramo), resultando un total de 100 interpolaciones.
El método de interpolación utilizado es el de splines cúbicas con condición de aceleración inicial y final constantes, que genera las coordenadas independientes de los puntos interpolados de cada tramo. Las coordenadas dependientes se obtienen resolviendo las ecuaciones de restricción no lineales con el método de Newton-Rhapson.
El método de las splines cúbicos es muy continuo, por lo que si se desea modelar una trayectoria en el que haya al menos 2 movimientos claramente diferenciados, es preciso hacerlo en 2 tramos y unirlos posteriormente. Sería el caso en el que alguno de los motores se desee expresamente que esté parado durante el primer movimiento y otro distinto lo esté durante el segundo movimiento (y así sucesivamente).
Obtenido el movimiento, se calculan, mediante fórmulas de diferenciación numérica, las velocidades y aceleraciones independientes. El proceso es análogo al anteriormente explicado, recordando la condición impuesta de que la aceleración en el instante t= 0 y en instante t= final, se ha tomado como 0. Las velocidades y aceleraciones dependientes se calculan resolviendo las correspondientes derivadas de las ecuaciones de restricción.
En esta tercera validación del modelo, se revisa la coherencia del movimiento interpolado.
Modelo 2, con análisis dinámico inverso
La dinámica inversa calcula, para un movimiento definido —conocidas la posición, velocidad y la aceleración en cada instante de tiempo y conocidas las fuerzas externas que actúan (por ejemplo el peso)— qué fuerzas hay que aplicar en los motores (donde hay control) para que se obtenga el citado movimiento. En la dinámica inversa, cada instante del tiempo es independiente de los demás y tiene una posición, una velocidad y una aceleración y unas fuerzas conocidas.
En este caso concreto, se desean aplicar, de momento, sólo las fuerzas debidas al peso, aunque se podrían haber incorporado fuerzas de otra naturaleza si se hubiese deseado.
Las posiciones, velocidades y aceleraciones, proceden del cálculo cinemático. El efecto inercial de las fuerzas tenidas en cuenta (el peso) es calculado. Como resultado final del análisis dinámico inverso, se obtienen los pares que han de ejercer los cuatro motores para replicar el movimiento prescrito con las fuerzas que estaban actuando.
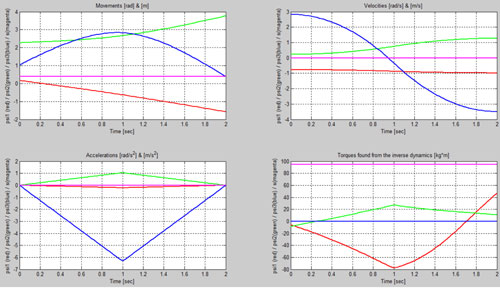
Modelo 2, con análisis dinámico directo
La cuarta validación del modelo consiste en confirmar que el movimiento obtenido por aplicar los pares obtenidos en la dinámica inversa, coinciden con el obtenido en el análisis cinemático (movimiento teórico). Para ello, es necesario acudir a la dinámica directa.
La dinámica directa se encarga de calcular el movimiento del robot, resultante de aplicar unos pares en motores y unas fuerzas en el robot.
Por lo tanto, el movimiento real resultante, al no haber cambiado ninguna condición de las obtenidas en la dinámica inversa (pares de motor y fuerzas inerciales debidas al peso de los eslabones) ha de ser el mismo al movimiento teórico. Siendo así, se considera que el modelo del robot generado está listo para trabajar.
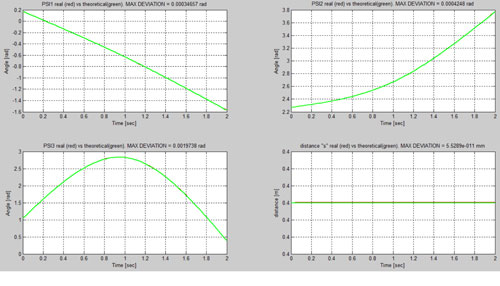
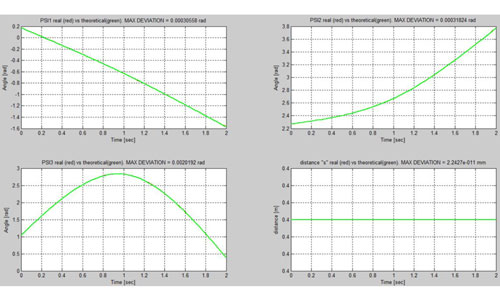
Modelo 2, con control de lazo cerrado
Si se introduce una fuerza exterior de mecanizado no contemplada en la dinámica inversa y se asigna en los motores los mismos pares resultantes de la resolución del problema dinámico inverso, el movimiento real obtenido no es igual al movimiento teórico.
El control de lazo cerrado se basa en ir comparando el movimiento real con el deseado e introducir las correcciones necesarias para minimizar o anular las diferencias.
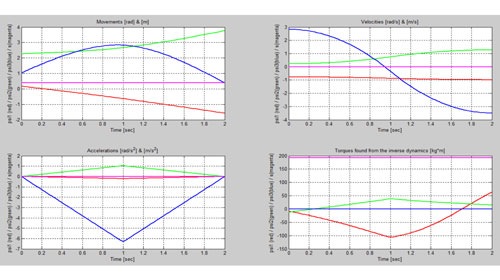
Figura 10. Movimientos, velocidades, aceleraciones Qmec = -35 kg (t>1,8 s), Kpos=0, Kvel=0.
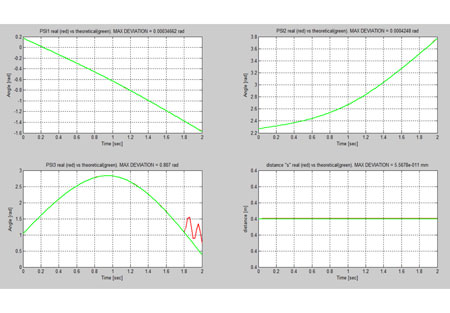
Figura 11. Detalle ángulos y distancia para Qmec = -35 kg (t>1,8 s), Kpos=0, Kvel=0.
Se aplican ganancias en forma de correcciones en posición y/o velocidad para eliminar esas diferencias. Se evalúa el error de posición como la diferencia, en cada punto, entre el movimiento teórico deseado en el modelo cinemático y el movimiento real obtenido para cada fuerza de mecanizado y una ganancia concreta.
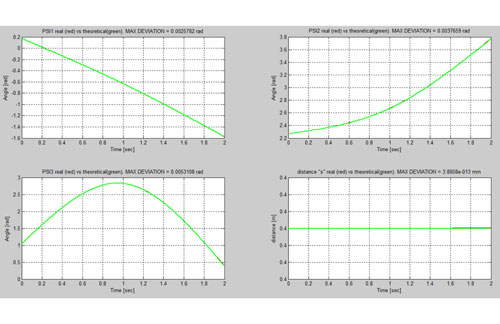
Figura 12. Detalle ángulos y distancia para Qmec= -70 kg (t>1,8 s), Kpos=10.000, Kvel=0, tintegración= 74,125 s.
Resultados
Finalmente se mapea el error de posición obtenido para cada fuerza de mecanizado y las diferentes ganancias previstas, graficando la mejor precisión que puede dar el robot para cada operación que se le requiere, y en qué condiciones.
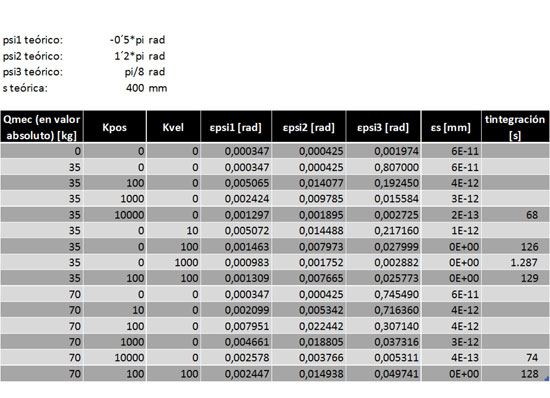
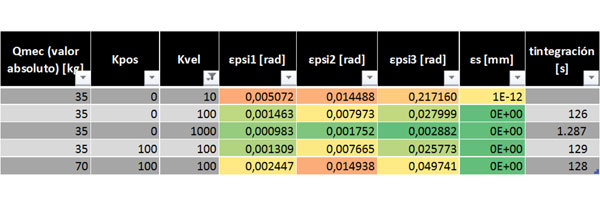
Las gráficas que se consideran interesantes son:
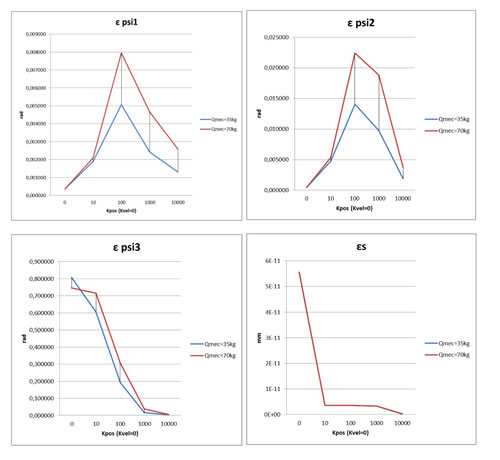
Conclusiones y posibles aplicaciones
Las conclusiones obtenidas son:
- Cuanto mayor es la fuerza de mecanizado que se precisa, el error es mayor para una misma ganancia; la ganancia tiene que ser aumentada para minimizar el error.
- Si se aplica una ganancia, la mejora se produce en todas las coordenadas.
- Es necesario aplicar valores altos de ganancia de posición, en torno a 10.000 para reducir de forma importante los errores.
- La ganancia de velocidad aplicada con valores de ganancia de posición 0, no tiene un efecto significativo y penaliza gravemente el tiempo de respuesta si toma valores altos.
- La ganancia de velocidad en valores bajos, combinada con ganancia alta de posición, da buenos resultados.
- Si el control de lazo cerrado fuese lo suficientemente rápido en dar la respuesta, podría llegarse a tolerancias de posición equiparables a los CNCs.
Las posibles aplicaciones detectadas son:
- Se está interesado en estudiar las posibilidades de apoyo en el mecanizado mediante robots en fábrica. Tiene sus dificultades, porque son mucho más flexibles, pero presentan ventajas en cuanto a la economía, equilibrado de ciclos de mecanizado, e incluso incorporación directamente a las células de fundición.
- Como futuras líneas de investigación en ese sentido, dentro de un programa de doctorado (en curso), a la vista de los resultados obtenidos, es:
- Prueba inicial real en fábrica sobre robot industrial.
- Estudio teórico; comportamiento con movimiento en 2 etapas (en cada etapa, algún motor estaría inactivo); aplicación de otros mecanizados; análisis del robot con trayectorias interpoladas con condición de velocidad inicial y final 0; modelización como sólido no rígido; y diseño del modelo de robot estándar antropomórfico de 6 grados de libertad.
- Aplicación a modelo real en fábrica.
Referencias
- Ferreras Higuero, E. Caracterización de un robot para aplicaciones de mecanizado con requerimientos de tolerancias. ETSII-UPM. Máster de Especialización de Ingeniería Mecánica, 2014
- García de Jalón de la Fuente, J. Análisis cinemático y dinámico de sistemas multicuerpo 3-D: aplicación a la dinámica vehicular. Mecánica Computacional, Máster de Ingeniería Mecánica. ETSII-INSIA, 2009.
- García de Jalón de la Fuente, J: Interpolación y aproximación de funciones. ETSII-UPM Departamento de Matemática Aplicada a la Ingeniería Industrial; 2014.
- García de Jalón de la Fuente, J., Bayo, E. Kinematic and Dynamic Simulation of Multibody Systems. Springer-Verlag, New York, 2011.
- García de Jalón de la Fuente, J., Shimizu, N. Matlab programs for kinematic and dynamic multibody simulation. ETSII-UPM and Motion Labo Inc, 2007.
- García de Jalón de la Fuente, J., Shimizu, N. Numerical Methods for Kinematic and Dynamic of 3D Multibody Systems. ETSII-UPM and Motion Labo Inc, 2007.



































































