Simulación de aplicación aerográfica de pintura sobre plástico

Fernando Varela López y Arantza Odriozola González
Cemitec - Centro multidisciplinar de innovación y tecnología de Navarra- Fundación Cetena15/10/2006

En la actualidad es indiscutible la importancia que están teniendo las piezas pintadas de plástico en la fabricación de componentes para automoción. Así como se han alcanzado mejoras considerables en la calidad de los materiales y de los procesos de inyección, la aplicación de piezas de plástico para fines estéticos o su integración con otros materiales ha requerido un esfuerzo considerable de parte de los fabricantes de pintura así como de los aplicadores.

Dentro de los diversos procesos de aplicación, el más extendido en el ámbito de piezas inyectadas es la aplicación aerográfica. En particular, debido a su impacto en el acabado final de las piezas, este análisis se centra en la aplicación de recubrimientos líquidos.

El proceso en sí mismo presenta tanto ventajas como desventajas respecto a otras alternativas:

Ventajas:

Es posible aplicar capas de pintura de un espesor relativamente bajo.
El acabado superficial es muy satisfactorio.
Permite trabajar con formas de piezas muy diferentes en la misma instalación.

Desventajas:

Las instalaciones suelen ser costosas
El “overspray” (pintura que es atomizada pero que es desaprovechada).
La gestión de los VOCs (componentes orgánicos volátiles) y residuos sólidos.

Pese a sus desventajas, es el sistema más práctico a la hora de aplicar pintura sobre piezas inyectadas. El aplicador debe asumir en muchos casos el coste extra debido al overspray como gastos indirectos relacionados al proceso. De la misma forma, el exceso de pintura necesario para el funcionamiento del proceso repercute en una gestión de residuos más compleja.

Por todas estas razones, resulta necesario optimizar la aplicación aerográfica de pintura. En ocasiones, esto es posible adaptando el proceso a las condiciones específicas de operación. En este delicado proceso intervienen tanto variables del proceso mismo (tipo de boquillas, instalación, extracción de nieblas) como de los materiales que se utilizarán: el sustrato (grado de limpieza/activación de la superficie, estática) y la pintura (tensión superficial, grado de mojabilidad sobre el plástico, efectos reológicos). Esta conjunción de factores hacen que el proceso de puesta a punto de una instalación requiera una considerable inversión de tiempo y recursos. Por esa razón, en este trabajo se introducirán las herramientas de simulación disponibles para poder optimizar este proceso de una forma rápida y eficiente, reduciendo el número de ensayos y el tiempo de puesta a punto.

El método de optimización se basa en la simulación computacional de fluidos, o CFD (Computational Fluid Dynamics). Partiendo de la base que el proceso de aplicación aerográfico es un problema fluidodinámico (en el que intervienen varias fases fluidas), las técnicas CFD permitirán reproducir en el ordenador el comportamiento de la pintura desde que sale de la pistola hasta que impacta sobre el sustrato sólido, formando la capa de recubrimiento líquido. En las siguientes secciones se detallan los fundamentos físicos que intervienen en la formación de la niebla de pintura y de qué manera esa niebla es afectada por el flujo de aire generado. Además, se señalan las bases del esquema computacional a partir del cual se puede predecir el comportamiento de la pintura en un proceso industrial real.

Caracterización físico-química de recubrimientos

El primer paso antes de desarrollar el modelo consiste en caracterizar de forma adecuada el recubrimiento líquido. Diversas propiedades de la pintura influyen en la formación de gotas, en particular:

La viscosidad a altas cizallas
La tensión superficial dinámica

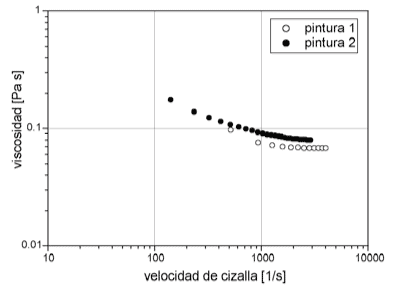
Es bien sabido que la viscosidad de las pinturas no es constante a lo largo del proceso, ya que depende de las condiciones de cizalla. Por esa razón, las medidas típicas de viscosidad (usualmente mediante copa Ford) no son suficientes, y la pintura debe caracterizarse mediante curvas reológicas, las cuales reflejan esta dependencia. En la figura 1 se muestran los resultados para pinturas utilizadas típicamente en este tipo de procesos.

En el límite de altas cizallas la viscosidad alcanza un valor constante, y es ése valor el que suele describir mejor el comportamiento de la pintura a la salida de la boquilla de pulverización. Valores típicos de viscosidad van desde los 20 hasta los 100 mPa s.

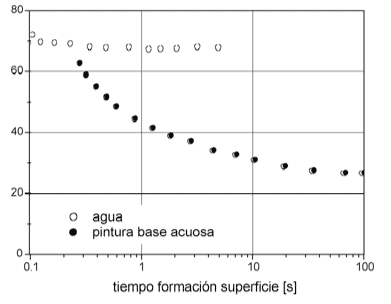
Las medidas reológicas se complementan con la determinación de la tensión superficial dinámica. Así como el concepto de tensión supercial indica la situación de equilibrio entre el líquido que forma parte de la interfase y las fuerzas cohesivas del seno del líquido, la tensión dinámica surge en aquellos casos en que la velocidadde formación de superficie es rápida respecto a la migración de aditivos desde el seno del líquido a la interfase. En estos casos es posible contar con una tensión superficial mucho más alta que la medida de manera estática. Esta diferencia se hace más importante en el caso de trabajar con pinturas de base acuosa, en las que la formación de superficie es rápida. En estas circunstancias, los aditivos tienen menos oportunidades de participar de la formación y coalescencia de gotas en la niebla. Una vez creada la película sobre el sustrato, tienen el tiempo suficiente para migrar y reducir la tensión superficial, logrando un acabado satisfactorio. Sin embargo, para la modelización de la formación de niebla, es necesario conocer el valor a frecuencias de creación de superficie altas. En la figura 2 se muestra el resultado para una pintura aerográfica de base acuosa. Además, se compara el comportamiento con un líquido puro (en este caso agua bidestilada).

Los datos obtenidos para la pintura son complementados con medidas de las condiciones aeráulicas del flujo de aire comprimido a través de la pistola; a partir de esto, se cuenta con todo lo necesario para la puesta en marcha del modelo computacional de procesos aerográficos.

Figura 1: Viscosidad de dos pinturas de aerografía

Flujo de aire a través de la pistola

El proceso físico que da lugar a la pulverización de la fase líquida en pequeñas gotas, así como la migración de estas gotas desde la pistola hasta el recubrimiento, está determinado, además de por las propiedades de la pintura vistas anteriormente, por las condiciones fluidodinámicas que se generan en la boquilla de la pistola. El diseño de cada sistema de pulverización (desde los más sencillos hasta los sistemas HVLP o tipo vortex) está pensado para generar un tipo determinado de niebla y una forma definida para cada necesidad. Sin embargo, estas consideraciones generalmente son afectadas por variaciones en las propiedades de la pintura, variaciones en el caudal de aire, envejecimiento del equipo, etc).

En la práctica, la utilización de un tipo particular de pistola está más cerca del “arte” que de la ingeniería, y el operario es quien, basado en horas y horas de uso, es capaz de lograr los resultados más satisfactorios. De forma de poder comprender mejor estas desviaciones y conocer de qué forma afecta la pintura y las condiciones de operación a la niebla generada, se plantea un modelo computacional que comprenda todas las variables y que permita predecir el comportamiento de un sistema de pulverización dado.

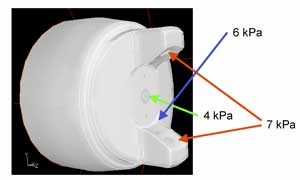
En la figura 3 se muestra un sistema de pulverización tradicional, en el cual la pintura es inyectada por gravedad. La presión de operación es de alrededor de 2 bar, con un sistema de regulación tanto de la presión de aire como del caudal de pintura pulverizado. Para la modelización, es necesario conocer, además, la presión a la salida de la boquilla, que es donde se crean las condiciones que determinarán la distribución de gotas que formarán la niebla. Estos valores han sido determinados experimentalmente mediante manómetros piezoeléctricos, encontrándose ligeras variaciones entre cada una de las salidas, debido al diseño particular de esta boquilla. El caudal de aire generado, así como el flujo de aire en el volumen considerado, queda perfectamente

determinado en el modelo. Los valores se muestran en la figura 4.

La boquilla utilizada para la creación del modelo está pensada para la creación de una hoja bien definida en una dirección, contrariamente a otros dispositivos aerográficos más sencillos. Esto se logra mediante el direccionamiento de diferentes chorros de aire que fuerzan el cono de aire central en una dirección y lo expanden en otra, creando un jet plano.

Las velocidades de aire a 15 cm de la pistola demuestran el carácter altamente anisótropo del campo de velocidades, encontrándose diferencias notables en cada una de las direcciones acimutales del flujo de aire. Los resultados de las mediciones servirán para la validación del modelo mostrado en la sección 4.

Figura 2. Tensión superficial dinámica de una pintura de base acuosa.

Figura 3: Sistema de pulverización HVLP

Figura 4: Presiones en la boquilla del sistema HVLP

El modelo fluidodinámico

El flujo de aire en la zona cercana a la boquilla está caracterizado por velocidades del orden de los 70 m/s. En estes régimen, el aire está en un régimen de turbulencia desarrollada la cual da lugar a un complicado patrón de flujo fluctuante, como puede apreciarse durante la utilización de cualquier sistema de aplicación aerográfica. Debido al esquema numérico que se va a plantear para desarrollar la pulverización de la fase líquida, es deseable contar con una descripción estacionaria, que sin embargo capte en promedio las fluctuaciones originadas en el flujo real. Esto se logra mediante un modelo de turbulencia RANS (Promedio estocástico de Navier-Stockes), en particular el modelo K-e. Como resultado, se cuenta con un campo de velocidades estático, realizado a través de un promedio en el tiempo del flujo más detallado. Si bien es una proximación, resulta adecuado para la determinación de la dinámica de las gotas.

La segunda parte de la modelización consiste en establecer un esquema numérico basado en fase discreta: la niebla estará descripta por un número de gotas generadas en la boquilla según un modelo estadístico. La evolución de esta gotas estará regida por la velocidad inicial del jet, así como por las fuerzas de arrastre viscoso debidas al aire. Estas últimas serán las responsables en última instancia de formación de la hoja. La distribución de tamaños afecta el arrastre de las partículas, concentrando o diluyendo la densidad media de pintura de la niebla.

Como resultado, se consigue establecer un modelo en el cual:

La velocidad del aire generado por la pistola es conocido en todo el espacio.
Las partículas de la niebla son identificadas y se calcula se trayectoria hasta que impactan sobre el sutrato.
Durante el vuelo, se admite la posibilidad de coalescencia y rotura de gotas según leyes semi-empíricas.
Finalmente, se contabilizan las gotas que impactan sobre el sustrato, las cuales pasan a formar parte de la película de acreción de pintura.

De esta manera, es posible establecer el espesor de pintura depositado durante el lapso definido por la actuación de la pistola. Esta predicción se comparó con aplicaciones experimentales en laboratorio, encontrándose un ajuste satisfactorio. En la figura 5 se muestra la validación experimental del modelo fluidodinámico, mientras que en la figura 6 puede verse alguno de los resultados obtenidos a partir del modelo, que describen el comportamiento de la niebla para las condiciones de operación antes mencionadas.

En la figura 7 puede verse una comparación entre una aplicación aerográfica experimental (derecha) y el resultado de la predicción. El resultado es satisfactorio, considerando que no se ha tenido en cuenta en la modelización más que una caracterización muy sencilla de la niebla. El modelo puede mejorarse de forma que tenga en cuenta otras variables como la evaporación de disolventes. Así mismo, es posible extender su aplicación a otros procesos de pulverización como la aplicación electrostática.

El modelo recoge las características principales del diseño del sistema de pulverización, así como las propiedades de la pintura, integrándolo bajo un único modelo, lo cual garantiza resultados confiables y verificables. Además, permite conocer en detalle la influencia que una pintura tiene en el proceso. Esto tiene particular importancia en los casos en que se esté realizando la migración de sistemas de base disolvente a sistemas de base acuosa: la dinámica de formación de niebla es completamente diferente en estos casos.

Conclusiones

La simulación de procesos aerográficos se basa en dos principios fundamentales: la determinación del campo de velocidades del aire y la modelización de la formación y dinámica de gotas. Ambos pasos pueden conseguirse en un esquema de flujo turbulento RANS para describir en promedio el campo de velocidades, así como un modelo estocástico de formación de gotas y el trazado de trayectorias, tratando a las mismas como una fase discreta.

Este procedimiento representa una herramienta importante para el diseñador de equipos e instalaciones de pintado aerográfico, ya que permite realizar ensayos de manera virtual y predecir el comportamiento de un sistema de aplicación en diversas circunstancias, probar nuevos materiales, etc. Para el aplicador, resulta útil a la hora de poner a punto sus procesos, extender el rando de aplicación de un sistema de aplicación, o mejorar la productividad establenciendo cambio en la forma de aplicar. Todos estos ensayos pueden realizarse de forma virtual, ahorrando tiempo y recursos, además de no interferir con el desarrollo productivo.

Artículo basado en el trabajo presentado en las 9as Jornadas de Plásticos en Automoción organizadas por el Centro Español de Plásticos