Superficies y formas complejas: siempre un reto

¿Pero, a qué se le llama superficies o formas complejas? Se podría pensar que una geometría de este estilo es aquella que a simple vista una persona piensa que es rara ya que no está formada por geometrías sencillas como cubos, cilindros y demás. Pues bien, no estaría muy alejada esa respuesta de la realidad, ya que esas geometrías son elementos que se pueden catalogar como superficies regladas, ya sean desarrollables (conos, cilindros) o no desarrollables (esferas), y son relativamente fáciles de generar mediante procesos de mecanizado. En cambio, el resto de superficies que no están englobadas en esos dos tipos se pueden catalogar como superficies libres, lo que implica una dificultad intrínseca en el mecanizado, ya que no permite, a priori, técnicas de fresado de flanco, lo que lleva a tener que acabar dichas superficies mediante copiados de bola.

Las superficies y formas libres son ese gran misterio que se quiere resolver el mundo del mecanizado a la hora de optimizar los procesos productivos en cuanto a tiempos de mecanizado y vida útil de herramienta. Esto se debe a que este tipo de geometrías son cada vez más frecuentes en el sector industrial, como, por ejemplo, en matrices de forja y estampación, o bien en numerosos componentes del motor aeronáutico, como los rotores de álabes integrados (IBRs) y demás componentes rotativos del motor.

La fabricación de este tipo de geometrías complejas se puede realizar a través de dos alternativas diferentes, una está estrechamente relacionada con la optimización de las trayectorias de mecanizado mediante el uso de algoritmos matemáticos que adapten esa superficie a una más sencilla de mecanizar, y la otra está relacionada con nuevos procesos, como complemento o reemplazo del proceso tradicional. La implementación de algoritmos matemáticos en el cálculo de las trayectorias de mecanizado no sólo genera trayectorias más sencillas, sino que, además ayuda en la reducción de tiempos de mecanizado y por ende en el coste. Por ello, el CFAA lleva trabajando los últimos años conjuntamente con BCAM (Basque Center for Applied Mathematics) en el desarrollo y verificación de algoritmos que permitan la implementación de técnicas de Flank Milling en dichas superficies.

Trabajos previos

La primera colaboración entre la Escuela de Ingenieros de Bilbao con BCAM fue a finales del año 2016, cuando se juntaron para analizar la posibilidad de implementar el cálculo matemático en la generación de trayectorias. Un primer acercamiento fue diseñar un algoritmo que fuese capaz de, dada una superficie compleja de forma libre y una herramienta cónica como datos de partida, calcular una superficie reglada desarrollable lo más parecida a la superficie de referencia en la que poder aplicar la técnica de acabado de Flank Milling.

Para demostrar la viabilidad de la implementación de este algoritmo matemático se mecanizaron una serie de álabes tanto con las trayectorias generadas por el algoritmo como por las trayectorias de un software comercial de CAM. Los resultados obtenidos dieron una gran esperanza al demostrar una mejora no sólo en cuanto al tiempo de mecanizado, sino que también en el acabado de las piezas. Esto se apreció en que mientras que el software comercial necesitaba 10 pasadas para acabar el álabe entero, el algoritmo matemático podía hacerlo en sólo tres pasadas [1].

Trabajo actual

Uno de los últimos trabajos en los que se está trabajando en torno a la implementación de algoritmos matemáticos es en el mecanizado de un engranaje espirocónico usando una técnica novedosa de mecanizado, que es el fresado de doble contacto. Este enfoque apunta a un contacto de doble tangencia entre la herramienta y la geometría de referencia, teniendo un contacto teórico a lo largo de dos curvas, en contraste con el tradicional fresado de flancos donde el contacto de la superficie de la herramienta se logra sólo a lo largo de una sola curva.

Este algoritmo, aparte de calcular las trayectorias de mecanizado para que se dé el fresado de doble contacto, requiere de una herramienta especial que se adapte a dicha geometría, en este caso la cavidad interdental de los dientes del engranaje. Esta herramienta también se calcula en el algoritmo y posteriormente se mecaniza para recubrirla con partículas abrasivas y poder usar la técnica de mecanizado super abrasivo. En resumidas cuentas, a diferencia del trabajo previo que se realizó en los álabes, no sólo la trayectoria, sino la forma propia de la herramienta es una incógnita en el algoritmo. En esta investigación conjuntas entre centros [2] se demostró que los engranajes espirocónicos poseen una geometría tal que puede ser fresada por doble contacto por herramientas de forma libre con una precisión alta.

Descripción del algoritmo

El algoritmo matemático se divide en 2 etapas, entre las que se encuentran la aproximación (i) y la optimización (ii). En la primera etapa, en la de aproximación, lo primero que se realiza en la división de la superficie de la cavidad interdental en dos mitades (S1, S2), las cuales son calculadas mediante la bisectriz (B) de la superficie de forma libre. Después, se genera una nueva superficie reglada (R) que se adapte a las superficies generadas por el corte con la bisectriz. La superficie reglada está constituida por una familia de líneas rectas de un solo parámetro y puede parametrizarse como R(s, t), donde el parámetro s está en la dirección de la línea y t es el tiempo (o pseudotiempo).

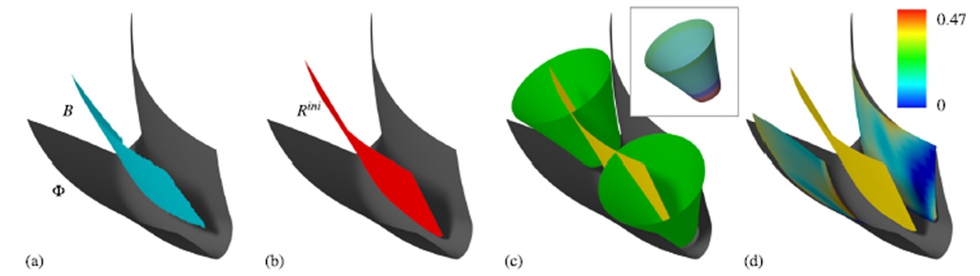
Para realizar una primera aproximación de la geometría de la herramienta hay que seguir el siguiente proceso: partiendo de un valor fijo de s, se calculan los puntos más próximos a las superficies S1 y S2. Estos puntos serán las aproximaciones de las superficies regladas a la superficie primitiva de la cavidad interdental. Mediante ese cálculo se obtienen 2 funciones de distancia d1(t) y d2(t). A continuación, se realiza una división de las funciones en n muestras y se promedia los valores, de esta manera se obtienen una primera aproximación de la geometría de la herramienta, para un valor específico de s. Aplicando esto para varios valores de s, se obtiene una función radial r(s) que describe una familia de esferas; su envolvente será la forma inicial de la herramienta.

Una vez concluida la etapa de aproximación, se procede con la optimización simultánea tanto de R (Superficie Reglada) como de r(s). Los puntos de control de ambas variables son las variables de optimización. La función objetivo tiene varios fines que cumplir, tales como un término que intenta encontrar las distancias iguales a S1 y S2, o el requerimiento de que el eje se mueva perpendicularmente a su dirección.

Próximos trabajos entre el CFAA y BCAM

Otro de los campos que se ha querido abordar es la fabricación eficiente y altamente precisa de geometrías curvas como las transmisiones de los automóviles, cajas de cambio, tornillos sin fin y otras piezas de motor de doble curvatura, ya que suponen un gran desafío en muchas industrias como la automotriz o la aeronáutica. Por ello, al igual que se hizo en el caso de estudio del engranaje espirocónico, se está estudiando la posibilidad de fabricar tornillos sin fin mediante el mecanizado superabrasivo. Para lo cual se aplicará un algoritmo similar que calcula tanto las trayectorias de mecanizado como la geometría óptima de la herramienta para el caso de estudio.

El tornillo sin fin se trata de una máquina de desplazamiento positivo provista de dos rotores helicoidales paralelos, un rotor macho y un rotor hembra, que se engranan el uno con el otro mientras giran. La interacción conserva el contacto tangencial que, debido a la naturaleza helicoidal de ambas partes, se logra a lo largo de una hélice. Esta hélice de contacto cambia con el tiempo, lo que resulta en que el fluido/gas confinado en las cavidades se transfiere en dirección axial. La geometría de los tornillos sin fin puede variar dependiendo del número de lóbulos de cada uno, del perfil básico del rotor y de las proporciones relativas de cada segmento de lóbulo del rotor, aunque geométricamente los límites de los tornillos sin fin son siempre superficies helicoidales.

En este proyecto se va abordar tanto el cálculo de las trayectorias y geometría óptima de la herramienta como de la fabricación de los tornillos sin fin y herramientas para el mecanizado superabrasivo. Concretamente, en un primer acercamiento se van a fabricar un par de tornillos sin fin, siendo un par de ellos simétricos y los otros no simétricos.

A la par que se están estudiando el fresado de doble contacto también se está investigando otros campos en torno a los componentes de superficies y formas complejas, como es la reducción del ‘jerk’ o sobreaceleración en las operaciones de acabado. Esto se debe a que la cinemática, que es la encargada de controlar las velocidades, aceleraciones y sobreaceleraciones de los movimientos de la máquina, juega un papel muy importante en el mecanizado. Tener un movimiento de accionamiento suave y con las mínimas sobreaceleraciones es fundamental, ya que afecta directamente a la calidad del mecanizado, en términos de rugosidad, por ejemplo. Los movimientos de accionamiento suaves (es decir, el perfil de avance suave) conducen a una menor variación del espesor de la viruta y, por tanto, a una menor desviación de la superficie mecanizada. Por el contrario, valores altos de jerk en los accionamientos corresponden a una aceleraciones y desaceleraciones repentinas en el movimiento que inducen vibraciones no deseadas, que pueden provocar daños en la herramienta y/o la pieza de trabajo.

Al fin y al cabo, se trata de un problema común que se da en el fresado de flanco de 5 ejes en superficies complejas y es que la tasa de variación de velocidad de los ejes rotativos de la máquina es muy elevada. Esto se debe a que la superficie que se va a mecanizar debe estar siempre en contacto con todo el flanco de la herramienta (en contraste con el proceso de copiado en el que sólo el extremo de la herramienta está en contacto con la superficie). Como resultado, los movimientos de los ejes representan variaciones instantáneas para ajustar la orientación de la superficie mecanizada en función de la complejidad del perfil de la pieza. Por otro lado, los programadores comerciales de CNC suelen considerar un avance programado para todas las líneas de comando del código G de mecanizado. Esto lleva a un escalado del avance de la trayectoria operativa cuando las velocidades de los ejes rotativos superan el límite de avance programado ya establecido en el código G. El escalado del avance de la trayectoria da lugar a derivadas de avance discontinuas y, por lo tanto, a altos valores de aceleración y sobreaceleración no deseados.

Proyecto COPTER

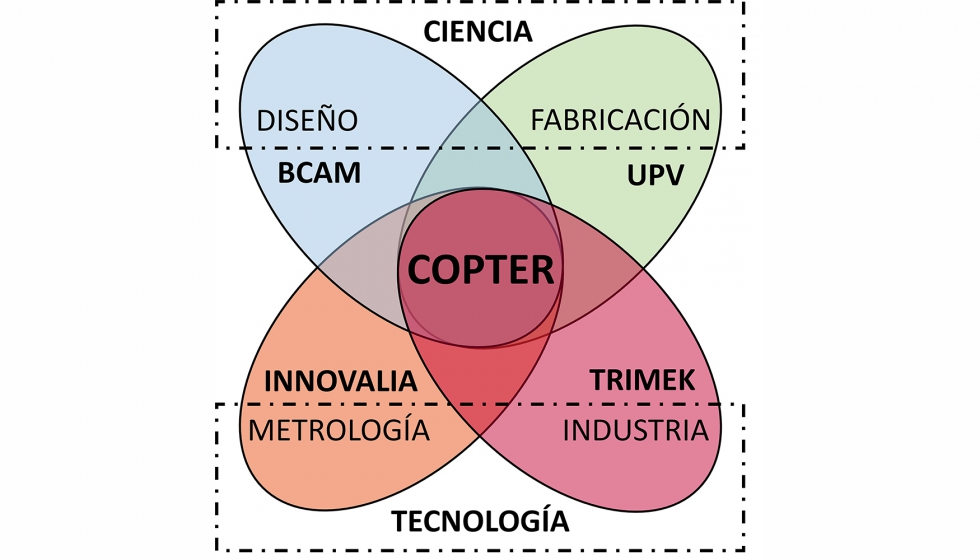
En relación a los componentes con superficies de geometrías complejas, no sólo importa cómo se fabrican, sino que también es importante como se miden para saber si cumplen o no con los requisitos geométricos establecidos. En esta línea, la Universidad del País Vasco UPV/EHU y BCAM junto con Innovalia y Trimek se han juntado en un Elkartek bajo el acrónimo COPTER, ‘Metrología aplicable a geometrías de alta complejidad para transmisiones de ultraprecisión’.

Este proyecto se presenta como una solución al diseño, fabricación e inspección de componentes formados por superficies de forma libre, en concreto trasmisiones de ultraprecisión. El proyecto se centra en investigar de manera completa las tecnologías de modelización cinemática de trasmisiones de ultraprecisión, en los fundamentos de los procesos de mecanizado de superficies libres en máquinas multi-eje, para configurar una plataforma que permita a empresas fabricantes de máquinas acceder al mercado de grandes trasmisiones de ultraprecisión especiales en series muy cortas o unitarias, y a los usuarios resolver la fabricación de esta tipología de superficies de manera competitiva y con excelentes ratios de calidad y fiabilidad. Con el trascurso del proyecto se pretende que el desarrollo tecnológico del mismo tenga un efecto multiplicador al poder ser transferido a la industria vasca a través de las instalaciones del CFAA (Centro de Fabricación Avanzada Aeronáutica) y el Centro de Competencias en Soluciones Avanzadas de Control de Calidad que operan la UPV/EHU y la Asociación de Innovalia respectivamente. Los resultados de este proyecto deben encontrar a través de estas estructuras abiertas de innovación el camino hacia productos y procesos de fabricación avanzada que mejoren la competitividad del tejido empresarial vasco y la capacidad de internacionalización de dichos productos.

Referencias

[1] Calleja, A.; Bo, P.; González, H.; Barton, M.; López de Lacalle, L. N. “Highly accurate 5-axis flank CNC machining with conical tools”. Int J Adv Manuf Technol, 97, 1605–1615 (2018). https://doi.org/10.1007/s00170-018-2033-7

[2] Bo P.; González H.; Calleja A.; López de Lacalle L.N.; Barton M., “5-axis double-flank CNC machining of spiral bevel gears via custom-shaped milling tools– Part I: modelling and simulation”, Precision Engineering, 62, 204-212 (2020)