Cómo obtener modelos 3D a partir de proyecciones axonométricas
(1) Departamento de Informática e Ingeniería Industrial. Universitat de Lleida. (2) Departamento de Expresión Gráfica en la Ingeniería. Universitat Politècnica de Catalunya15/05/2003
En los departamentos de informática e ingeniería industrial de la universidad de Lleida y en el de Expresión Gráfica en la ingeniería de la Universidad Politécnica de Cataluña se ha estudiado un nuevo método, basado en lógica proposicional multivaluada, para interpretar y comprender dibujos de objetos poliédricos formados por vértices triédicos. El objetivo es obtener modelos 3D a partir de proyecciones axonométricas.
La interpretación espacial de líneas de dibujo es un tema estudiado por las comunidades de Visión Artificial y Geometría Estructural. Éstas desarrollan algoritmos para automatizar la obtención de modelos 3D a partir de dibujos 2D tales que, como sucede con la visión humana, sean capaces de rechazar imágenes imposibles.
En este trabajo partiremos del sistema de etiquetado de Huffman [1] y Clowes [2], que asigna a cada línea o arista de una representación axonométrica R una etiqueta que denota si la arista es convexa, cóncava o de frontera u oclusión. El sistema asigna una etiqueta de tipo + a aquellas aristas que son convexas y en las que las caras que concurren en la arista son visibles en la representación R; asigna una etiqueta de tipo - a aquellas aristas que son cóncavas y en las que las caras que concurren en la arista son visibles en la representación R; y asigna una etiqueta de tipo (‡fl, ) a aquellas aristas en las que únicamente es visible una cara de las que concurren en la arista. Estas últimas serán las aristas frontera y las caras que concurren en la arista presentarán una oclusión.
Por otra parte, en función del número de aristas que concurren en un vértice y su posición en la representación, el sistema de Huffman y Clowes clasifica las uniones en los vértices. Las uniones pueden ser de cuatro tipos: L, Y, T y F. Además, como las aristas que concurren en un vértice tienen etiqueta, estos cuatro tipos de uniones dan lugar a un catálogo que está formado por 18 uniones que representan todas las uniones que son físicamente realizables en una escena poliédrica 3D. Si una proyección axonométrica admite un etiquetado de las aristas consistente con las uniones del catálogo de Huffman y Clowes, entonces podemos obtener un modelo 3D. En cambio, si el etiquetado es inconsistente, la proyección corresponde a un objeto poliédrico 3D físicamente irrealizable. Sin embargo, cabe mencionar que el conjunto de proyecciones axonométricas posibles con el catálogo de Huffman y Clowes no es completo, en el sentido que se han estudiado extensiones del mismo [3] que hacen válidas ciertas proyecciones que con el catálogo de Huffman y Clowes no son válidas.
Fórmulas multivaluadas
Definición 2. Una interpretación es una función del conjunto de variables proposicionales al conjunto de valores de verdad. Un interpretación satisface un MV-literal S :p si el valor que asigna a p se encuentra en S, satisface una MV-cláusula si satisface al menos uno de sus MV-literales y satisface una MV-fórmula si satisface todas sus MV-cláusulas.

Definición formal del problema
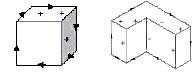
1. El dibujo bidimensional es una proyección axonométrica de una unión de objetos tridimensionales. Los objetos tridimensionales son objetos poliédricos, donde cada vértice es la intersección de exactamente tres planos. La figura 1 muestra proyecciones axonométricas válidas de dos objetos poliédricos.
2. Cada línea del dibujo representa una arista de uno de los poliedros. Se ignoran sombras, líneas ocultas y zonas de cambio de color.
Una interpretación particular del dibujo se obtiene al etiquetar todas las aristas del mismo de manera consistente. Este etiquetado nos informa sobre si las aristas son cóncavas o convexas o bien si son aristas que unen dos caras de las cuales sólo una es visible en la proyección axonométrica.
Después de considerar las diferentes formas en las que podemos formar vértices triédricos y los diferentes puntos de vista desde donde pueden ser observados, Huffman y Clowes obtuvieron el catálogo de 18 vértices posibles que pueden aparecer en una proyección axonométrica (ver la figura 2). Dentro de un vértice, numeramos sus aristas empezando por la que se encuentre en su posición superior izquierda, y avanzando en el sentido de las agujas del reloj.
Codificación mediante una MV-fórmula

2. El conjunto de variables proposicionales, Var, es el conjunto { v | v in V }. Cada variable representa un vértice distinto de la proyección axonométrica.
3. El conjunto de MV-cláusulas de la fórmula es la unión de diferentes conjuntos de MV-cláusulas. Una interpretación que satisfaga la fórmula nos dará un etiquetado válido para los vértices de la proyección. Las MV-cláusulas aseguran que el etiquetado asignado a un vértice es consistente con el de sus vértices vecinos, según el catálogo de la figura 2. Como la especificación completa de las cláusulas es muy larga, aquí nos limitamos a describir un subconjunto particular de las mismas. Consideremos el caso donde queremos asegurar que el etiquetado para un vértice v1, que es de tipo F, sea consistente con el del vértice v2, que es de tipo Y, porque se encuentran conectados mediante una arista común en las posiciones de las aristas v1i y v2i de los vértices v1 y v2, respectivamente. Tendremos un conjunto diferente de tres MV-cláusulas, en función de las posiciones de la arista en los dos vértices (v1i y v2i). Estos son los casos posibles:


Funcionamiento
En el primer ejemplo partimos de una proyección donde inicialmente sólo están etiquetadas las aristas de frontera, es decir, aquellas que confluyen en un vértice donde una de las caras no es visible. En la figura 3a mostramos la proyección con el etiquetado inicial. A partir de este etiquetado inicial, nuestro método va determinando las etiquetas únicas para este ejemplo que son consistentes con el catálago de vértices posibles. Por ejemplo, en el vértice tipo Y que se encuentra más a la derecha de la proyección vemos que debido al etiquetado inicial la única forma de etiquetar las tres aristas que confluyen en ese vértice es mediante un arista convexa (+). La aplicación reiterada de este proceso de propagación de restricciones lleva finalmente a la situación que vemos en la figura 3b. El problema es que este etiquetado final no es consistente. Esto se debe a que un vértice (el vértice con el signo de interrogación) no es un vértice posible de nuestro catálogo y por lo tanto nuestro método nos indica que esta proyección no corresponde a un objeto 3D.
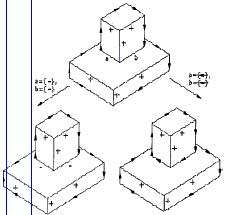
En el segundo ejemplo, que vemos en la figura 4, también partimos de una proyección inicialmente etiquetada por sus aristas frontera. Sin embargo, existen dos aristas (aristas a y b) que inicialmente no etiquetamos como de frontera porque admiten otro posible etiquetado. En la parte superior de la figura 4 mostramos la proyección con el etiquetado que determina nuestro método a partir del etiquetado inicial. Las aristas a y b quedan sin determinar puesto que admiten dos posibles etiquetados. En este punto nuestro método decide como completar el etiquetado escogiendo valores posibles y consistentes con el catálogo para las aristas a y b. Una primera elección determina las aristas a y b como cóncavas lo que le lleva a un etiquetado completo y consistente. Este etiquetado interpreta la proyección como la proyección de un único objeto 3D. La segunda elección determina las aristas a y b como de frontera lo que también le lleva a un etiquetado completo y consistente. En este caso, este etiquetado interpreta la proyección como la proyección de dos objetos 3D.
Complejidad
Referencias
[2] M.B. Clowes, “On seeing things”, Artificial Intelligence 2: 79-116, 1971.
[3] C. Ansótegui et al., “Resolution methods for many-valued CNF formulas”, SAT Conference, 2002
[4] T. Kanade, “A theory of Origami world”, Artificial Intelligence 64: 147-160, 1980.
[5] D.Waltz, “Understanding line-drawings of scenes with shadows”, in: The Psychology of Computer Vision, McGraw-Hill, 19-91, 1975
[6] L.M. Kirousis, C.H. Papadimitriou, “The complexity of recognizing polyhedral scenes”, Journal of Computer and System Sciences 37: 14-38, 1988.