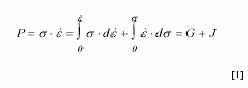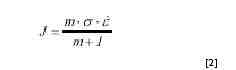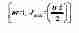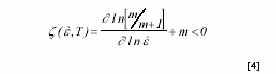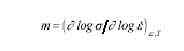INTRODUCCIÓN

MÉTODO EXPERIMENTAL

RESULTADOS Y DISCUSIÓN

CONCLUSIONES

REFERENCIAS

El presente trabajo se centra en el desarrollo de los mapas de inestabilidad plástica de un acero microaleado de medio carbono durante un proceso de forja en caliente. En estos mapas se delinean las regiones óptimas de forja y las de inestabilidad plástica que hay que evitar en un proceso de forja en caliente. La base para la construcción de los mapas de inestabilidad es el modelo dinámico de los materiales.

Uno de los procesos de fabricación de componentes mecánicos más utilizados en la industria es la forja en caliente. El problema más importante que surge en el diseño de este proceso es lograr el control de todos los parámetros (temperatura, velocidad de deformación, grado de reducción, etc.). Por ello, el diseñador del proceso debe tener un conocimiento global de la interacción existente entre la microestructura y los parámetros de control.

Para conseguir esta meta industrial se pretende, en este trabajo, desarrollar el mapa de inestabilidad plástica de un acero microaleado de medio carbono. En este mapa se delinean las regiones óptimas de forja y las de inestabilidad plástica que hay que evitar en un proceso de forja en caliente.

La base para la construcción de los mapas de procesado que se efectuará en este trabajo es el llamado "modelo dinámico de materiales" desarrollado por Prasad y col. [1,2] y revisado por Gegel y col. [3,4] y Alexander [5]. A una velocidad de deformación dada, la energía total disipada, s. , consta de dos partes. En la terminología de la modelización de sistemas [6] se representa por la suma de dos integrales:

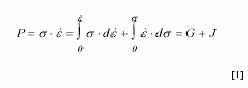
donde G es el contenido disipador y J es la función complementaria de G. En cada instante, la disipación de energía ocurre mediante un aumento de temperatura (el contenido G) y un cambio microestructural (el co-contenido J) y la partición de energía entre los dos se decide mediante el coeficiente de sensibilidad a la velocidad de deformación (m) de la tensión de fluencia (s). A una temperatura y una deformación dada, el co-contenido disipador J viene dado por [1,2]:

donde es la velocidad de deformación. El co-contenido disipador J del material, que es un dispador no-lineal, puede normalizarse con un disipador lineal para definir un parámetro adimensional llamado eficiencia de la disipación de energía (h) a través de los procesos metalúrgicos:

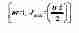
La variación de h, generalmente expresada en porcentaje, con la temperatura y velocidad de deformación representa las características de disipación de energía mediante los cambios microestructurales en la pieza conformada y constituye el mapa del procesado. Este mapa de procesado exhibe varios dominios que pueden ser correlacionados con mecanismos microestructurales específicos.

El modelo dinámico de materiales se basa en los principios de la termodinámica irreversible aplicada a la mecánica continua de la fluencia plástica a grandes deformaciones descrita por Ziegler [7]. Kumar [8] y Prasad [2] desarrollaron un criterio continuo combinando estos principios con los de la separabilidad de la disipación de energía y mostraron que, en un proceso de conformado en caliente, la inestabilidad plástica ocurre cuando:

donde m es el de sensibilidad a la velocidad de deformación,, de la tensión de fluencia definido como

La variación de z con T y con constituye el mapa de inestabilidad mediante el cual se pueden delinear las regiones donde el parámetro z toma valores negativos, y por tanto delimita las zonas a evitar en el proceso de conformación.

Para simular el proceso de forja, se llevaron a cabo ensayos de compresión en caliente de un acero comercial microaleado de medio especialmente destinado al sector de forja de componentes de automoción. Los elementos microaleantes son V, Ti y Al y su composición química se indica en la Tabla I.

Tabla 1. Composición química del acero estudiado (% en peso).

Para estudiar su comportamiento a fluencia se realizaron ensayos de compresión uniaxial a velocidades de deformación verdadera constantes. Los ensayos se efectuaron a temperaturas que oscilaron entre 1150ºC y 900ºC a incrementos de 50°C, y en un intervalo de velocidades de deformación que varió entre 10-4 y 10 s-1. Se usaron tres sistemas de ensayos: un equipo electromecánico para ensayos a velocidades < 0,3 s-1, un equipo servohidráulico para = 1 y 3 s-1 y un plastómetro por leva para =10 s-1.

Las probetas ensayadas eran cilíndricas (su eje era paralelo al de laminación) de 11,4mm de altura y 7,6mm de radio. Con estas dimensiones se conseguía minimizar los prácticamente inevitables problemas de abarrilamiento y pandeo. Las probetas se austenitizaban durante 5 minutos a 1200ºC (la velocidad de calentamiento fue de aproximadamente 1ºC s-1) y entonces se enfriaban hasta la temperatura de ensayo a una velocidad de enfriamiento de 2ºC s-1 aproximadamente. Detalles adicionales sobre la realización de los ensayos pueden encontrarse en las referencias [9] y [10].

Las curvas de fluencia obtenidas en este trabajo tienen la tendencia habitualmente observada en los materiales que sufren restauración y recristalización dinámicas: la tensión aumenta muy rápidamente (endurecimiento por deformación del material) hasta alcanzar un máximo después se mantiene o decrece de manera monótona o con oscilaciones, a causa de la recristalización dinámica (R. D.), tanto de pico simple como de pico cíclico. En algunas situaciones (a altas velocidades y bajas temperaturas) apenas se observó ablandamiento posterior a la tensión de saturación, poniéndose de relieve que el único mecanismo de ablandamiento operante entonces era la restauración dinámica.

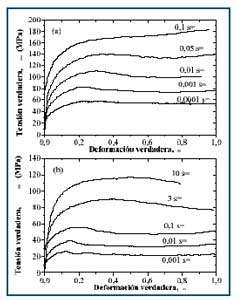
En la figura 1 se muestra una selección de las curvas de fluencia obtenidas a temperaturas 900 ºC y 1150 ºC y diferentes velocidades de deformación. Un primer hecho notable a resaltar es la equivalencia, por lo que a las características mecánicas se refiere, del efecto de disminuir la temperatura o aumentar la velocidad de deformación.

Los mapas de disipación de energía se determinan en base a datos experimentales de fluencia en un amplio rango de temperaturas y velocidades de deformación, usando los principios del modelo dinámico de materiales [1-5]. Las curvas log(s) vs log() se ajustaron a un polinomio de segundo grado, y el coeficiente de sensibilidad a la velocidad de deformación, m, se determina a partir de la pendiente en cada punto de la curva.

En la figura 2 se representan los mapas de disipación de energía obtenidos a deformaciones 0,2, 0,4 y 0,6 del acero estudiado. En esta figura, a e= 0,2, y a modo de ilustración, la variación 3-D de la eficiencia de disipación de energía con la temperatura y la velocidad de deformación se representa como mapa 3-D, y para una mejor visualización se muestra para las demás deformaciones solo los mapa de contornos de iso-eficiencia en el plano de velocidad de deformación - temperatura.

Figura 1. Curvas de fluencia del acero estudiado a (a) 900ºC y (b) 1150ºC

Los mapas obtenidos a diferentes deformaciones varían sensiblemente con la deformación y a medida que aumenta van apareciendo nuevos dominios en el mapa. Esto quiere decir que la deformación afecta sensiblemente a los mapas de procesado obtenidos, lo cual es lógico ya que diferentes mecanismos de ablandamiento están operando a distintas combinaciones de temperaturas, velocidades de deformación

Los mapas de eficiencia del acero estudiado, obtenidos a deformaciones 0,2, 0,4 y 0,6, y representados en la Fig. 2, exhiben las características siguientes [9,10,13].

1) En el mapa de eficiencia energética correspondiente a la deformación 0,2 (Fig. 2a) sólo se aprecia un dominio con un máximo de eficiencia de aproximadamente 36 % extendido sobre el rango de temperaturas de 1000 a 1075 ºC y velocidad de deformación de 10-4 s-1. La observación de las curvas de fluencia [9,10] muestra que a e= 0,2 sólo tiene lugar la recristalización cíclica cuando la deformación se efectúa a bajas y T altas. La restauración dinámica como único mecanismo de deformación está por venir y la R. D. de pico simple todavía no ha empezado para otras combinaciones de T y . Por consiguiente, el dominio bajo consideración corresponde a R. D. cíclica.

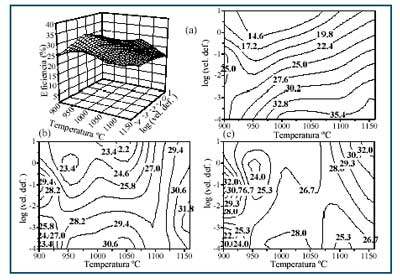
Figura 2. Mapas de disipación de energía obtenidos a deformación (a) 0,2, (b) 0,4 y (c) 0,6

Las curvas de fluencia obtenidas en este trabajo tienen la tendencia habitualmente observada en los materiales que sufren restauración y recristalización dinámicas: la tensión aumenta muy rápidamente (endurecimiento por deformación del material) hasta alcanzar un máximo después se mantiene o decrece de manera monótona o con oscilaciones, a causa de la recristalización dinámica (R. D.), tanto de pico simple como de pico cíclico.

2) A altas deformaciones (0,4 y 0,6) los mapas de contornos de iso-eficiencia energética cambian de aspecto (ver Fig. 2b y 2c). A e = 0,4 el dominio inicial de la recristalización se divide en dos, uno centrado en 1050 ºC y 10-4 s-1 y otro en 1150 ºC y 0,002 s-1 extendido hacia altas. El primer dominio es lo que queda del área de recristalización cíclica anteriormente comentado, mientras que el segundo dominio corresponde al nuevo campo de la R. D. de pico simple. Esto se entiende mejor observando el mapa correspondiente a e = 0,6 (Fig. 2c), que es aproximadamente la deformación correspondiente a fluencia de estado estable. Ahora el nuevo dominio se ha trasladado hacia altas velocidades de deformación (10 s-1 y 1150 ºC) y el dominio de la R. D. cíclica ha desaparecido prácticamente, como en ambos casos era de esperar.

La variación del parámetro de inestabilidad con la temperatura y la velocidad de deformación a deformaciones de 0,2, 0,4 y 0,6 se representa en la figura 3.

Las regiones del mapa donde el parámetro es negativo, se consideran como regiones inestables de fluencia [2,11,12], y no se recomiendan para la conformación de los dos aceros estudiados. Observando la evolución de los mapas de inestabilidad con la deformación es interesante hacer notar que, generalmente, en los dominios caracterizados por un pico de eficiencia en los mapas de procesado, el parámetro de inestabilidad toma sus valores máximos. Al contrario, en los dominios caracterizados por un mínimo de eficiencia, toma sus valores mínimos. En el mapa de inestabilidad correspondiente a la deformación e = 0,6 se destaca que el dominio de alta temperatura y alta velocidad de deformación es el dominio más estable de todo el mapa.

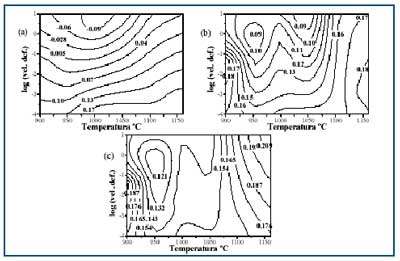
Figura 3. Mapas de contornos del parámetro de inestabilidad a las deformaciones (a) 0,2, (b) 0,4 y (c) 0,6

Foto: Uddelhom

En el mapa de variación del parámetro de inestabilidad con la temperatura y la velocidad de deformación correspondiente a la deformación 0,2 aparece un dominio a bajas y intermedias temperaturas y altas velocidades de deformación con un parámetro de inestabilidad negativo (ver Fig. 3a) lo cual supondría que esto dominio es una zona de inestabilidad microestructural [2,11,12]. Puesto que las observaciones mediante MEB [9] no evidenciaron ninguna manifestación de inestabilidad la única explicación que se puede dar a los valores negativos del parámetro de inestabilidad es la siguiente: la inestabilidad que predicen estos mapas puede ser debida al efecto térmico o calentamiento adiabático y no se puede atribuir dicha inestabilidad a las bandas de cizalladura ya que al recristalizarse el material estudiado se producen cambios estructurales que hacen desaparecer a estas bandas.

* Se han determinado los mapas de procesado del acero estudiado. En estos mapas se ha podido observar los diferentes dominios que representan los fenómenos de la restauración y la R. D., y a medida que cambia la deformación, los mapas de disipación de energía evolucionan y cambian su aspecto.

* El dominio de la R. D. es muy importante en la optimización de la conformabilidad intrínseca, puesto que reconstituye la microestructura mediante la formación y la migración de limites de grano y es el mecanismo más eficiente dentro de la región segura del procesado. Por consiguiente, en los mapas de disipación de energía, el dominio de la R. D. pondrá los limites para el control de los parámetros del proceso de conformado. Los parámetros óptimos de procesado de los dos aceros estudiados a diferentes series de ensayos son aquellos que corresponden al dominio de la R. D. de pico simple. A deformación e=0,6, el dominio de la R. D. está centrado a 1150 ºC y 10 s-1 con una eficiencia de 33% mientras que el de la restauración dinámica está centrado a 900 ºC y 10-1 s-1.

* Los mapas de inestabilidad indican que las regiones donde se prevé la aparición de los procesos de restauración dinámica y la R. D. son las regiones más estables del mapa. En estas regiones el parámetro de inestabilidad toma valores positivos y alcanza sus máximos en los dominios representantes del proceso de la R. D. de pico simple. Lo cual es enteramente consistente con que los dominios de la R. D. de pico simple son los dominios más estables de los mapas de procesado

[1] Y.V.R.K. Prasad, H.L. Gegel, S.M. Doraivelu, J.C. Malas, J.T. Morgan, K.A. Lark y D.R. Barker. Metall.Trans., vol 15A, pp 1883, (1984).

[2] Y.V.R.K. Prasad. Indian Journal of Technol., vol 28, pp 435, (1990).

[3] H.L. Gegel, J.C. Malas, S.M. Doraivelu y V.A. Shende en Metals Handbook, ASM, Metals Park, Ohio, vol 14, (1987).

[4] H.L. Gegel, J.C. Malas, S.M. Doraivelu, J.M Alexander y J.S. Gunasekera en Advanced Technology of Plasticity, vol 11, (1987).

[5] J.M. Alexander en Modelling of Hot Deformation of Steel, Ed. Springer-Verlag, Berlin, (1984).

[6] P.E. Wellstead en Introduction to Physical Systems Modelling, Ed. Academic Press, Londres, (1979).

[7] H. Ziegler en Progress in solid mechanica, Ed. I.N. Sneddon y R. Hill, New York, vol 4,(1963).

[8] A.K.S. Kumar. M.Sc (Eng) Thesis, Indian Institute of Science, Bangalore, (1987).

[9] A. Al Omar. Tesis Doctoral, Universidad Politécnica de Cataluña, Barcelona, (1996).

[10] A. Al Omar, J.M. Cabrera y J.M. Prado. Scripta Metall. et Mater., vol. 34, nº8, pp. 1303-1308. (1996).

[11] N.Srinivasan y Y.V.R.K. Prasad. Metall. Trans. vol. 25A, pp. 2275, (1994).

[12] B.V. Radhakishna Bhat, Y.R. Mahjan, H.Md. Roshan y Y.V.R.K. Prasad. Mat. Sci. and Technology, vol 11, pp 167, (1995).

[13] J.M. Cabrera, E. Flores, A. Al Omar y J.M. Prado. 2º Simposium Internacional, ESIQIE. IPN, México. (1996).