Control de vibraciones en sistemas de mecanizado
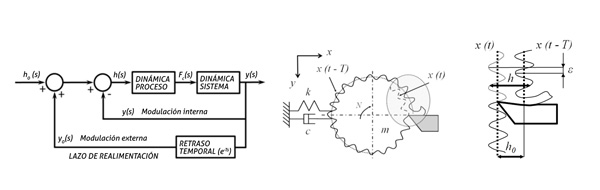
El sistema puede entonces modelizarse a través de una ecuación diferencial de 2º grado con retraso temporal T, siendo T el período de giro (dado por las revoluciones de pieza en torneado o por el giro de la herramienta en fresado):
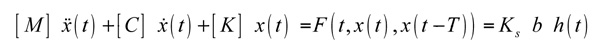
Esta ecuación permite describir el comportamiento dinámico del sistema a través de las características modales del sistema. Las matrices de masa [M], amortiguamiento [C] y rigidez [K] definen lo que se denomina función de respuesta en frecuencia (FRF), es decir, la representación matemática de la relación entre la entrada o esfuerzo de excitación de la estructura y la salida o deformación resultante del sistema de mecanizado, considerado lineal e invariante. Ks es el coeficiente de corte en la dirección de avance que relaciona la fuerza F con la sección instantánea de viruta Sc(t), definida ésta como el producto de la profundidad de corte por el espesor de viruta completo. En general, los términos del primer miembro de la ecuación varían en el tiempo (posición variable de los elementos móviles, reducción de la masa de la pieza, etc.) aunque pueden suponerse, bajo ciertas condiciones, como constantes. Por tanto, el carácter no lineal de la ecuación se supondrá esencialmente ligado a la naturaleza compleja de los esfuerzos de corte.
1.- Reducción y control de vibraciones
Dentro de los distintos métodos desarrollados para obtención de lóbulos de estabilidad (analíticos, numéricos, EF, etc.), los llamados mecanísticos o semi experimentales [Altintas 95] han tenido un éxito notable ya que simplifican la ecuación dinámica trasladándola al dominio frecuencial. Estos métodos se requieren ensayos de caracterización de herramienta de forma previa a su utilización como modelos predictivos. Partiendo de la figura 1, se define el espesor de viruta h(t) en un instante cualquiera como:
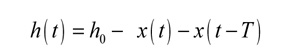
Donde h0 es el espesor de viruta estático o estacionario (igual al avance) y x(t)-x(t-T) es el espesor de viruta dinámico. Utilizando las propiedades de la transformada de Laplace, la expresión para el espesor de viruta dinámico como función del desplazamiento resulta como:
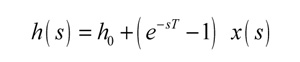
Para analizar cualitativamente si una determinada vibración tiene consecuencias sobre el comportamiento del sistema suele recurrirse al concepto anterior de FRF expresando la relación entre entrada y salida en el dominio frecuencial:
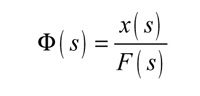
El significado físico de la FRF sería así el de la mayor o menor capacidad que tiene la estructura para transmitir la energía contenida en la señal de esfuerzo de la entrada, pudiendo contener una o más frecuencias fundamentales. Por tanto, el cociente entre la respuesta x(s) del sistema frente a la excitación F(s) será:
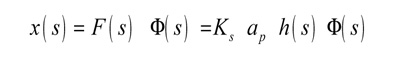
Sustituyendo esta expresión sobre la ecuación del espesor de viruta dinámico, se obtiene la función de transferencia en lazo cerrado:
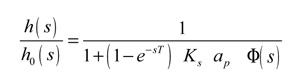
Para estudiar la estabilidad del sistema, deben evaluarse las raíces de la ecuación característica. Si se suponen ceros de la forma s=σ+jωc, pueden darse 3 situaciones posibles: raíces con parte real positiva (σ>0) -> sistema inestable; raíces con parte real negativa (σ< 0) -> sistema estable; raíces con parte real nula (σ=0) -> sistema críticamente estable. El estudio de vibraciones en el dominio de la frecuencia analiza la frontera entre los casos estables e inestables (σ=0) y sustituye dichas raíces (s=jωc) sobre la ecuación característica. Tras separar e igualar a cero las partes real e imaginaria y realizar las oportunas transformaciones trigonométricas, se obtienen 2 relaciones fundamentales:
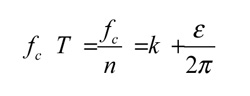
Donde se relacionan velocidad de giro del husillo n (en rps), frecuencia de chatter fc (en Hz) y desfase ε (en rad) entre ondas pertenecientes a períodos consecutivos, y:
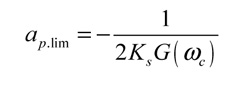
Donde G es la parte real de la función de transferencia. De forma resumida, los pasos a llevar a cabo en la obtención del diagrama de lóbulos son:
- Seleccionar una frecuencia de chatter ωc sobre la parte real negativa de la función de transferencia.
- Calcular el ángulo de fase ε del sistema para dicha ωc.
- Calcular la profundidad de corte límite ap, lim.
- Calcular la velocidad de giro N en [rpm] para los distintos valores enteros de k: 0,1, 2, etc.
- Repetir los pasos anteriores realizando un barrido de frecuencias ωc cerca de la frecuencia natural del sistema.
En el apartado anterior, se ha esquematizado la forma de obtener los lóbulos de estabilidad en un software predictivo. Sin embargo, a día de hoy las soluciones prácticas encontradas en la industria pueden dividirse en dos tipos fundamentales de software: los predictivos y los iterativos o por aprendizaje.
Enfoque predictivo
El enfoque predictivo se basa en resolver la ecuación dinámica que describe el comportamiento del sistema de corte. Dependiendo del tipo de resolución, se habla de métodos analíticos o temporales.
- Simulación analítica [Altintas 95, Budak 98]: los métodos analíticos o en el dominio de la frecuencia estudian la estabilidad de la ecuación dinámica del proceso de corte y responden a la formulación expuesta en el apartado 2.1. Son métodos rápidos computacionalmente pero que, a cambio, proporcionan escasa información sobre el proceso. En general, obligan a hipótesis simplificadoras: fuerzas lineales, geometrías de corte sencillas, no permiten incluir no linealidades etc. Se clasifican en 2 grandes grupos:
- Soluciones monofrecuencia y multifrecuencia: estudian las raíces de la ecuación característica del lazo cerrado del sistema de corte.
- Métodos numéricos: se apoyan en la teoría de Floquet analizando los autovalores de una matriz de transición entre 2 períodos consecutivos (semi discretización, colocación de Chebyshev, etc.)
- Simulación temporal [Tlusty 81]: se basa en la integración numérica de las ecuaciones del movimiento y permite introducir de forma precisa la cinemática del proceso, la geometría de corte de la herramienta y posibles no linealidades. En una simulación en el dominio del tiempo, se predicen las fuerzas y vibraciones para un conjunto específico de parámetros de corte y las señales resultantes (fuerzas y desplazamientos) se analizan para determinar la presencia de chatter. Si los análisis en el dominio de la frecuencia suponen que la herramienta siempre mantiene el contacto con la pieza, con simulaciones temporales los efectos no lineales pueden introducirse de manera directa y la predicción de la estabilidad será más precisa. De cara al estudio de la estabilidad, el mayor inconveniente es su gran coste computacional en comparación con los modelos analíticos. Para una velocidad de corte concreta, deben realizarse una serie de simulaciones bajo diferentes profundidades de corte con lo que el límite de estabilidad se calcula de forma iterativa. Para obtener el diagrama completo, el proceso se repite a distintas velocidades de corte.
Enfoque iterativo
El enfoque iterativo se basa en, partiendo de condiciones de corte inicialmente inestables, converger hacia una combinación de velocidad de corte y profundidad de pasada estables. En este tipo de métodos, se lleva a cabo una grabación sonora de la operación y se analiza y procesa para predecir unas nuevas condiciones de corte, fundamentalmente, una nueva velocidad de rotación. Ya se demostró en el apartado 2.1 (Ecuación 7) la fuerte relación entre la frecuencia de vibración y la velocidad de giro. Pues bien, los distintos programas comerciales disponibles en el mercado (Harmonizer, AccordMill) buscan ubicar una nueva velocidad de rotación situada en un submúltiplo de la frecuencia principal del sistema.
3.- Estrategia integral de control de vibraciones
Para poseer un buen dominio y control sobre el proceso de corte, se debe disponer de un buen modelo dinámico del conjunto husillo-porta-herramienta. Algunos sistemas están orientados a detectar problemas en tiempo real, ya sea por análisis temporal de las señales de corte [Suh 02] o por análisis frecuencial de señales acústicas captadas por micrófonos [Weingaertner 06], con lo cual el sistema ya habrá sufrido las primeras consecuencias de un mal corte. El otro enfoque es el predictivo basado en técnicas RCSA (Receptance Coupling Substructure Analisis). Pensando que en un taller hay numerosas combinaciones de máquina-husillo-porta-herramienta, el número de ensayos de caracterización modal (por ejemplo, de impacto con martillo) sería demasiado pesado. Es por ello que interesa disponer de un modelo representativo de los elementos herramienta, porta y husillo. Acoplando la función de respuesta dinámica de cada uno de ellos, puede conformarse un modelo dinámico de todo el conjunto. Por ejemplo, Namazi [Namazi 07] (figura 2a) modeliza el contacto cónico husillo-porta mediante resortes lineales y a torsión uniformemente distribuidos sobre la superficie de contacto. Filiz [Filiz 09] presenta un modelo de porta-herramientas incorporando técnicas espectrales de Chebyshev y teoría de Resistencia de materiales para obtener una solución paramétrica. La dinámica en punta de herramienta se completa con mediciones experimentales (figura 2b).
![Figura 2. a. Acoplamiento de receptancias para obtención de FRF en punta de herramienta [Namazi 07]; b... Figura 2. a. Acoplamiento de receptancias para obtención de FRF en punta de herramienta [Namazi 07]; b...](https://img.interempresas.net/fotos/829800.jpeg)
Otra forma efectiva de reducir o eliminar las vibraciones viene de la mano de incrementar la rigidez o el amortiguamiento. Los absorsores de vibraciones pueden ser pasivos o activos, mediante la participación de accionamientos que actúan sobre la estructura dada una consigna determinada. Se trata de subsistemas masa-resorte que se añaden a la estructura para modificar el comportamiento dinámico del sistema resultante y puede ser la solución a adoptar en sistemas de un grado de libertad.
Las herramientas con amplios voladizos son cada vez más habituales en todo tipo de aplicaciones, tanto para solucionar problemas de accesibilidad como para potenciar la productividad. Esto conlleva al mismo tiempo un aumento de la probabilidad de aparición de vibraciones. Tal es el caso de las largas barras de mandrinar (figura 3). Para conseguir buenas tasas de arranque de material a profundidades aceptables es común el empleo de herramientas amortiguadoras o silenciosas (Silent Tools de Sandvi) presintonizadas a una frecuencia concreta dependiendo del voladizo con el que se vaya a trabajar. También se pueden usar placas de metal duro o aleaciones de tungsteno sinterizado con 2-4% de cobre o níquel. Con ello, se consigue aumentar el módulo de Young y el amortiguamiento pudiendo la barra mecanizar de forma estable con relaciones de esbeltez de hasta L/D>7.

En este sentido, otro punto importante en cualquier taller de fabricación lo constituyen los dispositivos de amarre puesto que representan un volumen importante de gastos, tanto a la hora del diseño como por el espacio ocupado en el taller. El objetivo es restringir los desplazamientos en los puntos más problemáticos durante el mecanizado ya que cuando se manejan piezas flexibles o con paredes delgadas (gran superficie y bajo volumen) tienden a producirse problemas estáticos y dinámicos. Para piezas de geometría compleja es muy habitual el uso de amarres flexibles o reconfigurables, adaptados al contorno de la misma. Las empresas alemanas Schmalz o Kostyrka (grupo Roemheld) vienen desarrollando dispositivos de amarre de vacío adaptados a las necesidades específicas de cada pieza. Estos equipos trabajan por succión (ventosas) y tienen como ventajas reducidos tiempos de preparación y alta flexibilidad. La figura 4 muestra una placa-matriz para fijación de paneles delgados. También, el consorcio europeo Affix que aglutina a distintas universidades (Sheffield, Nottingham, etc.), centros tecnológicos (entre ellos, Fatronik) y compañías (Rolls Royce, Volvo, etc.) han desarrollado distintos dispositivos y patentes para fijación de piezas complejas, principalmente álabes y NGVs.
![Figura 4 a. Placa-matriz de Schmalz para fijación de paneles aeronáuticos; b. Utillaje tipo array de pines para sujeción de álabes [Phuah 05] c... Figura 4 a. Placa-matriz de Schmalz para fijación de paneles aeronáuticos; b. Utillaje tipo array de pines para sujeción de álabes [Phuah 05] c...](https://img.interempresas.net/fotos/829806.jpeg)
En primer lugar, deben realizarse los ensayos de caracterización los cuales permiten definir un coeficiente específico para el par herramienta de corte-material mecanizado. Aunque esta energía de corte se suele tomar como constante dentro de la zona normal de trabajo, en general, no tiene por qué serlo y deben realizarse ensayos en un amplio rango de trabajo para conocer la verdadera evolución de los coeficientes de corte con los parámetros velocidad de corte, profundidades axial y radial así como con el avance. También hay que distinguir entre coeficientes de corte correspondientes a una herramienta de geometría concreta y material y coeficientes de corte para herramienta-material. En este sentido, investigaciones recientes han conseguido calcular con buena precisión los esfuerzos generados por una fresa esférica a partir de coeficientes obtenidos por sencillos ensayos de corte ortogonal con una placa de tornear de la misma calidad [Altintas 96, Bissey 05], lo cual resulta muy interesante de cara a reducir el número de ensayos de caracterización para una misma familia de herramientas.
Una buena selección de las condiciones de corte pasa también por visualizar a priori, una vez obtenidos los parámetros modales del sistema y los coeficientes mencionados, las cartas de estabilidad y la evolución de la curva límite con las condiciones de corte. Esta es la verdadera utilidad de los diagramas de lóbulos: reconocer el aprovechamiento de ciertos espacios entre lóbulos e intentar acoplar estos condicionantes con las restricciones que impone el operario debido a las capacidades limitadas de la máquina. Una vez seleccionadas las condiciones de corte, deben probarse en condiciones reales de mecanizado. Anteriormente, deberán programarse trayectorias de herramienta que respeten la inmersión máxima permitida. En este sentido, ciertos autores vienen desarrollando intensos esfuerzos en intentar acoplar la información de los diagramas de lóbulos con programas tipo CAM (que únicamente resuelven el problema en su vertiente geométrica) como es el caso del profesor Altintas con el software MachPro.
A pesar de los altos niveles de calidad y reproducibilidad, la MH de control numérico aporta relativamente poca información sobre el proceso de corte por lo que deben exigirse mayores dosis de instrumentación y auto-evaluación que permitan detectar desgastes prematuros de herramientas, roturas de filo, vibraciones, colisiones, ausencia de herramienta/pieza, etc. Esto debe hacerse antes del corte, por ejemplo, a través de palpadores de pieza que refieran el programa al bruto y sondas de herramienta que permitan identificar si una herramienta está partida (antes o después de la ejecución del programa), pero sobre todo, a lo largo del proceso en tiempo real. La cantidad de información es más pesada de manejar pero permite una mejor comprensión del corte, la detección del mal funcionamiento y la detención a tiempo del programa. Con ello, se consiguen reducir costes debidos a parada de máquina, reparaciones, daños en amarres, etc.
Los distintos elementos o captadores se eligen en base a los siguientes criterios: coste bajo, de fácil instalación y mantenimiento, que no restrinjan el espacio de trabajo de la máquina ni los parámetros de corte, que no interfieran en la rigidez de la máquina, medición lo más cercana al punto de interés, adecuada precisión, sensibilidad y robustez.
En torneado, la vigilancia online se lleva a cabo a través de la medición de los esfuerzos de corte (Kistler, Brankamp). En torneado como en fresado, se utilizan mesas dinamométricas Kistler constituidas por captadores piezoeléctricos, tanto para caracterizar y trabajos de investigación como para detecciones online. También suele medirse la potencia y el par consumidos por el husillo (Artis, figura 5a; DigitalWay), tanto en fresado como en taladrado y roscado. Como ventajas, el uso de estas mesas aporta gran cantidad de información sobre el corte: pueden detectarse desgastes, roturas, obtener la frecuencia de vibración, etc. Sin embargo, son caras, reducen el espacio de trabajo y requieren adaptadores especiales para el amarre de pieza o herramienta. Por ello, no se utilizan habitualmente en producción.
Para resolver este inconveniente, es habitual encontrar cabezales instrumentados. Kistler ha fabricado un anillo que se monta intercalado entre la cubierta y el interior del husillo. Este captador integrado debe compensarse para que los primeros modos del conjunto rotativo no interfieran durante el giro del mismo. Ya se ha comentado que, en fresado, la medida de la potencia es una práctica muy frecuente ya que es una magnitud muy fácil de medir y a bajo coste. En el armario eléctrico, pueden colocarse captadores de efecto Hall que proporcionan la intensidad consumida. Al ser el ancho de banda limitado, esta magnitud es sólo un valor promedio. En controles numéricos más recientes, puede obtenerse información de la potencia consumida a través de parámetros internos obtenidos de los servomotores.
Por su parte, la medida de vibraciones se lleva a cabo bien con acelerómetros, piezoeléctricos de cuarzo o cerámicos que se utilizan profusamente por su pequeño peso, fácil manejo y precio bajo. Es importante elegir bien el lugar donde colocarlos así como el ancho de banda (varias decenas de kHz). El otro elemento típico de captura son los micrófonos. En este caso, el ancho de banda se amplía a los MHz. La medida de desplazamientos suele realizarse a nivel de la nariz del husillo utilizando captadores capacitivos [Altintas 02] o inductivos [Muller 02]. Tienen la ventaja de no interferir con el espacio de trabajo y poseen una gran precisión, hasta 0,1 mm. De hecho, suelen utilizarse para compensar las dilataciones térmicas del husillo de alta velocidad. Resultan, por otro lado, bastante caros.
El siguiente paso es el tratamiento de las señales en las cuales interesan los picos, valores promedio y eficaces, valores pico a pico, resultantes, niveles de dB o presiones acústicas en MPa. Las señales deben filtrarse con cuidado de cara a no distorsionar en exceso la señal original. La forma de asegurar que el proceso de corte marcha conforme a lo previsto es colocar un acelerómetro cerca del husillo que detecte la rotura o colisión de la herramienta a través de un pico que sobrepasa un umbral fijado (por ejemplo, si se sobrepasa la magnitud de la fuerza hasta niveles superiores al 300% respecto al corte normal). La determinación de este umbral no es fácil y suele hacerse de forma experimental. Como distintas etapas en el mecanizado de la pieza pueden referirse a umbrales diferentes, muchas máquinas disponen de modo de aprendizaje, durante el cual se lleva a cabo el mecanizado de una o varias piezas tests y donde deben establecerse los distintos niveles permitidos (curvas de aprendizaje) a cada etapa del proceso. Esta forma de proceder es habitual en la industria del automóvil y para grandes series. Para cadencias de producción más bajas como en aeronáutica, se adapta peor y se suele fijar un umbral único.
En la industria, deben adoptarse soluciones ágiles y fiables, que no distorsionen la zona de trabajo. En principio, el acelerómetro debe colocarse del lado del husillo y no sobre la mesa, ya que proporciona una magnitud más realista. En general, y debido al mantenimiento del husillo, estos captadores suelen tener que colocarse en el exterior del husillo (Fig.5b/c, sistema Spectra Pulse de Montronix) lo cual no es recomendable ya que además de señal de corte pueden introducirse señales provenientes de otros puntos.

Otro punto importante es el seguimiento y control del nivel vibratorio que permite proteger el deterioro de la herramienta y del husillo e igualmente garantizar una calidad geométrica de la pieza suficiente. Para las típicas máquinas de arranque de viruta y velocidades de rotación corriente, se suele utilizar el ‘criterio de la velocidad de oscilación’ (RMS), obtenida por integración de las señales brutas de aceleración en la banda de frecuencia entre 10-1.000 Hz (ISO 2372). La velocidad RMS da una buena idea de los esfuerzos generados durante el mecanizado, ya sea de vibraciones forzadas o de chatter. Por ello, muchos programas de vigilancia están basados en esta norma: VibroSmart (Vibrometer), VibroControl (Brüel & Kjaer). Suele establecerse un primer límite que para los avances de los ejes y un segundo más alto que ordena parar la rotación del husillo. Aproximadamente, un husillo debe girar en vacío con menos de 1 mm/s y en corte a no más de 7-8 mm/s. Valores superiores acortarán la vida del cabezal. El ancho de banda se suele fijar entre 10-1.000 Hz para máquinas convencionales (3.000-6.000 rpm) y se amplía a varios kHz en máquinas de alta velocidad, para integrar en el cálculo de la velocidad de oscilación los armónicos de la frecuencia de rotación del husillo. Para detectar de forma específica un caso de chatter, se puede utilizar un filtro de Kalman que elimine del espectro en frecuencias todos los armónicos correspondientes a la frecuencia de giro del husillo. Sin embargo, en este caso, hay que tener cuidado si la frecuencia de chatter está muy cerca de un armónico ya que puede quedar suprimida al no ser detectada.
3.- Aplicación: Torneado de pieza de baja rigidez y dinámica variable
A continuación, se presenta un caso de estudio llevado a cabo en la UPV/EHU donde se aplica la teoría expuesta anteriormente en torno a métodos predictivos al torneado de una pieza de baja rigidez y dinámica variable en el tiempo [Urbikain 12].
El uso de plaquitas redondas en el torneado de carcasas aeronáuticas es bastante común ya que son herramientas que permiten combinar distintas direcciones de mecanizado, ganando la operación en flexibilidad y accesibilidad. El caso de estudio expuesto a continuación se llevó a cabo sobre una pieza que se diseñó con forma de polea y cuyos parámetros modales iban variando a lo largo de las operaciones de mecanizado. El modelo de estabilidad desarrollado se basaba en un modelo de fuerzas de corte no lineal con coeficiente variables dependientes de la profundidad y de la velocidad de corte. Por otro lado, se realizó la suposición de pieza flexible en la dirección radial y herramienta rígida.
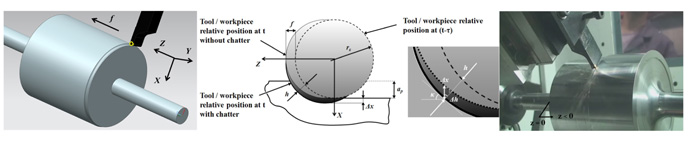
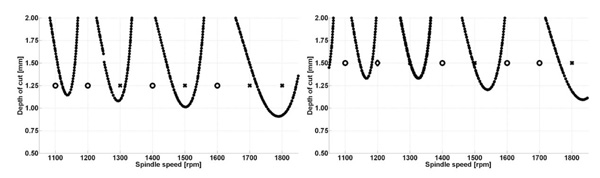
Para la verificación experimental, se realizaron distintas pasadas haciendo un barrido de velocidades. Antes de cada test de corte y para cada pasada, se obtuvieron los parámetros modales (promedio de 10 impactos) en 4 puntos de la periferia de la pieza. Las condiciones de algunos de los tests se muestran en las tablas 1 y 2 y la correlación entre modelo y resultados experimentales en las figuras 7 y 8.
Tabla 1. Parámetros modales de simulación: Casos 1 y 2
|
Distancia respecto al inicio del mecanizado [mm] & N [rpm] |
Caso 1: ap = 0,75 [mm] |
Caso 2: ap = 1,00 [mm] |
||||
|
Frecuencia |
Rigidez |
Amortig. |
Frecuencia |
Rigidez |
Amortig. |
|
|
f [Hz] |
k [N/m] |
ξ [%] |
f [Hz] |
k [N/m] |
ξ [%] |
|
|
z=-30 / 1.700-1.800 |
156 |
5,63e7 |
0,00850 |
157 |
5,92e7 |
0,00941 |
|
z=-60 / 1.500-1.600 |
156 |
5,71e7 |
0,00880 |
157 |
5,95e7 |
0,01018 |
|
z=-90 / 1.300-1.400 |
156 |
5,81e7 |
0,00907 |
157 |
6,32e7 |
0,01055 |
|
z=-120 / 1.100-1.200 |
156 |
6,18e7 |
0,00920 |
157 |
6,75e7 |
0,01088 |
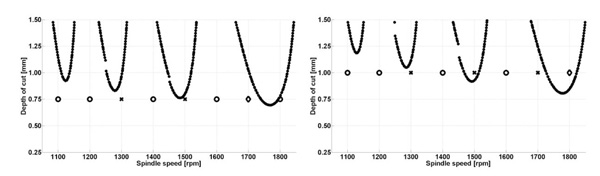
Tabla 2. Parámetros modales de simulación: Casos 3 y 4
|
Distancia respecto al inicio del mecanizado [mm] & N [rpm] |
Caso 1: ap = 0,75 [mm] |
Caso 2: ap = 1,00 [mm] |
||||
|
Frecuencia |
Rigidez |
Amortig. |
Frecuencia |
Rigidez |
Amortig. |
|
|
f [Hz] |
k [N/m] |
ξ [%] |
f [Hz] |
k [N/m] |
ξ [%] |
|
|
z=-30 / 1.700-1.800 |
158 |
6,51e7 |
0,00966 |
162 |
7,78e7 |
0,00991 |
|
z=-60 / 1.500-1.600 |
158 |
6,62e7 |
0,01009 |
162 |
7,85e7 |
0,01027 |
|
z=-90 / 1.300-1.400 |
158 |
6,50e7 |
0,01052 |
162 |
8,00e7 |
0,01076 |
|
z=-120 / 1.100-1.200 |
158 |
6,89e7 |
0,01023 |
162 |
7,92e7 |
0,01050 |
Referencias
- [Altintas 95] Y. Altintas, E. Budak. Analytical prediction of stability lobes in milling. Annals of CIRP, vol. 44 (1), pp. 357-362, 1995.
- [Budak 98] E. Budak, Y. Altintas. Analytical prediction of chatter stability in milling. Part I: General formulation; Part II: Application of the general formulation to common milling systems, Trans. of ASME, Journal of Dynamic Systems, Measurements and Control, vol. 120, pp.22-36, 1998.
- [Phuah 05] H. L. Phuah, Part-fixture behaviour prediction methodology for fixture design verification, Ph.D. thesis, University of Nottingham, School of Mechanical, Materials and Manufacturing Engineering, Nottingham, 2005.
- [Molfino 09] M. Molfino, R. Zoppi, D. Zlatanov, Reconfigurable swarm fixtures. Proceedings of the ASME / IFToMM International Conference on Reconfigurable Mechanisms and Robots, pp. 730–735, London: IEEE, 2009.
- [Bakker 10] O.J. Bakker phD, Control Methodology and Modelling of Active Fixtures, University of Nottingham, 2010.
- [Altintas 96] E. Budak, Y. Altintas, E.J.A. Armarego. Prediction of milling force coefficients from orthogonal cutting Data. Trans. ASME Journal of Manufacturing Science and Engineering, vol. 118, pp. 216-224, 1996.
- [Tlusty 81] J. Tlusty, F. Ismail. Basic nonlinearity in machining chatter, Annals of CIRP, vol. 30 (1), pp. 299-304, 1981.
- [Suh 02] C.S. Suh, P.P. Khurjekar, B. Yang. Characterisation and identification of dynamic instability in milling operation. Mechanical Systems and Signal Processing, vol.16 (5), pp.853-872, 2002.
- [Weingaertner 06] W.L. Weingaertner, R.B. Schroeter, M.L. Polli, J.O. Gomes. Evaluation of high-speed end-milling dynamic stability through audio signal measurements. Journal of Materials Processing Technology, vol. 179, pp.133-138, 2006.
- [Namazi 07] M. Namazi, Y. Altintas, T. Abe, N. Rajapakse. Modeling and identification of tool holder, spindle interface dynamics. International Journal of Machine Tools and Manufacture, vol. 47, pp.1333-1341, 2007.
- [Filiz 09] S. Filiz, C.H. Cheng, K.B. Powell, T.L. Schmitz, O.B. Ozdoganlar. An improved tool–holder model for RCSA tool-point frequency response prediction. Precision Engineering, vol. 33 (1), pp. 26-36, 2009.
- [Albrecht 05] A. Albrecht, S. Park, Y. Altintas, G. Pritschow. High frequency bandwidth cutting force measurement in milling using capacitance displacement sensors. International Journal of Machine Tools and Manufacture, vol. 45 (9), pp.993-1008, 2005.
- [Muller 02] M.K. Muller. On-line process monitoring in high speed milling with an active magnetic bearing spindle, Swiss Federal Institute of Technology, ETH Zurich, 2002.
- [Sandvik 06] Silent Tools, Sandvik Coromant, Sandviken, Sweden, 2006.
- [Urbikain 12] G. Urbikain, L.N.López de Lacalle, F.J. Campa, A. Fernández, A. Elías, Stability prediction in straight turning of a flexible workpiece by collocation method, International Journal of Machine Tools and Manufacture, vol. 54-55, pp. 73-81, 2012.















































































