Rediseño de la mangueta delantera del monoplaza eléctrico FSB2022 para su fabricación mediante tecnología aditiva
Xabier Cearsolo Aramberri, Mario Arrue Sanz, Juan Ramon Castillo Trigo, Maitane Gabilondo Nieto y Urtzi Gabiña Larrañaga. IMH – Campus
17/10/2022En este sentido, están surgiendo nuevos estándares de diseño, conocidos como Design for Additive Manufacturing (DfAM), para reducir las dificultades y los costes de fabricación mediante la optimización del componente para un proceso en particular [4]. El uso de DfAM permite aprovechar al máximo la libertad de diseño que proporciona la FA y cumplir con los requisitos establecidos. En los últimos años se han desarrollado diferentes herramientas que maximizan los beneficios y capacidades de fabricación que ofrecen las tecnologías de FA [5]. Estas incluyen programas de diseño, optimización topológica (TO), mallado y laminado 3D, simulación en servicio y de procesos. Entre estos programas se encuentran los que ya existían en el mercado y se han ido adaptando a las nuevas necesidades de la FA, pero también nuevas herramientas específicas que han ido surgiendo como consecuencia del desarrollo que se está produciendo en este ámbito [3].
En los últimos años, la variedad de herramientas software para la FA ha aumentado considerablemente debido a la libertad de diseño que ofrecen este tipo de procesos. Esta ventaja de las tecnologías FA permite crear formas orgánicas y geometrías complejas sin afectar en el coste o la complejidad de la fabricación. Las herramientas de optimización estructural son especialmente útiles en la FA ya que se utilizan para obtener estructuras ligeras y de alto rendimiento. Esto es especialmente relevante para industrias como la aeroespacial y transporte, donde las piezas deben cumplir con las especificaciones de las condiciones de carga en un espacio de diseño determinado. Las herramientas de optimización estructural brindan soluciones de diseño mediante la aplicación de modelos numéricos iterativos, basándose en diferentes algoritmos de cálculo.
Generalmente, la optimización estructural se divide en 3 categorías, que corresponden a optimización de tamaño, optimización de forma y TO [6]. Entre estos tres métodos de optimización, la TO se considera la más genérica porque puede generar nuevos diseños sin necesidad de disponer de uno predeterminado, lo que resulta de gran interés para los diseñadores de FA. La TO es una herramienta que proporciona un diseño de la pieza en función de los objetivos (normalmente minimizar la masa o maximizar la rigidez), requisitos de carga y restricciones de diseño establecidos. Los resultados obtenidos utilizando la TO sirven como referencia para la geometría final de las piezas fabricadas por FA [2], [3]. Después de llevar a cabo la TO, puede ser necesario ajustar la geometría de la pieza teniendo en cuenta las posibles operaciones de posprocesado. Por lo tanto, puede ser necesario añadir espesor en aquellas zonas donde se vaya a realizar un mecanizado posterior.
Por otro lado, las altas velocidades de calentamiento/enfriamiento y los grandes gradientes que se generan en la pieza durante la impresión con las tecnologías de FA pueden generar tensiones residuales y, en consecuencia, deformaciones en las piezas. El uso de herramientas de simulación para anticiparse a posibles problemas de impresión 3D es uno de los factores más importantes para la correcta aplicación de estas tecnologías. Estas simulaciones de procesos pueden proporcionar información útil que se puede utilizar para minimizar o evitar problemas de impresión, como es el caso de la optimización de los parámetros del proceso para minimizar las tensiones, la orientación adecuada de la impresión y la optimización del soporte. Además, las herramientas de simulación se pueden utilizar junto con otros programas de cálculo de elementos finitos para predecir el comportamiento de las piezas [3].
Desarrollo del proyecto
En este contexto, y en el marco del Título Propio de Especialización Universitaria en Fabricación Aditiva que se imparte en la Escuela Universitaria de Ingeniería Dual IMH-Campus, se ha desarrollado un proyecto cuyo objetivo consiste en el rediseño de la mangueta delantera del nuevo monoplaza 100% eléctrico FSB2022 del equipo Fórmula Student Bizkaia (en adelante FSB) de la Escuela de Ingeniería de Bilbao. El propósito del presente trabajo es doble, por un lado, aligerar el peso de la pieza, y por otro, analizar las diferentes fases de diseño que requiere la adopción de las tecnologías de Fabricación Aditiva para su fabricación, en este caso la tecnología Laser Powder Bed Fusion (LPBF).

Rediseño de la mangueta para su fabricación mediante FA
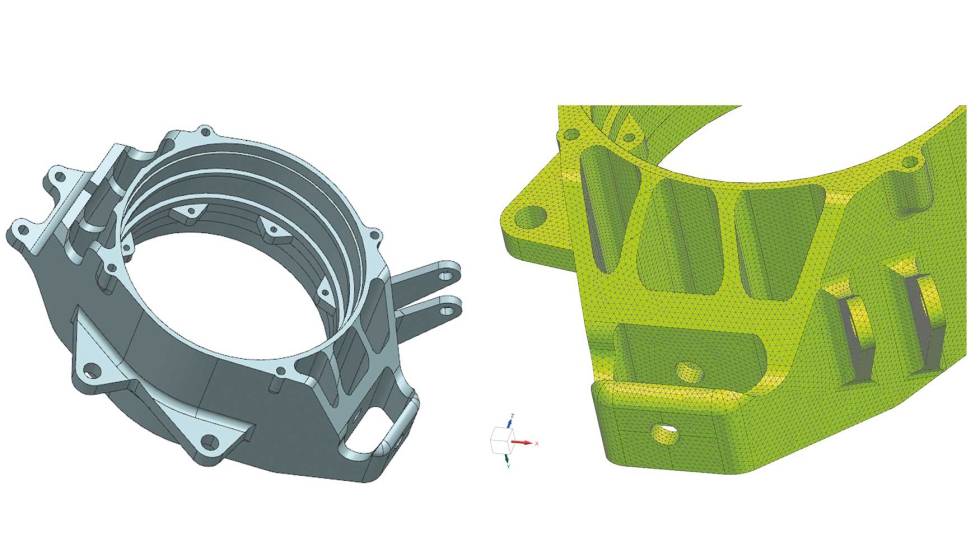
El primer paso ha consistido en analizar las propiedades mecánicas de la mangueta actual bajo la acción de todas las cargas aplicadas (suministradas por el equipo FSB) empleando la herramienta de software de análisis de elementos finitos Simcenter 3D integrado en el sistema NX de Siemens y ejecutando un estudio estático lineal. Para ello, y a partir del modelo inicial, se han realizado varias simplificaciones geométricas (radios de acuerdo pequeños, agujeros de pequeño diámetro, etc.) que permitirían obtener una mejor calidad de malla en toda la pieza (ver figura 2).
Las cargas aplicadas en el modelo se muestran en la siguiente tabla 1. Las fuerzas remotas como la de suspensión y la del peso del motor se han trasladado desde el punto de aplicación de la carga hasta la geometría de la mangueta empleando elementos tipo RBE3 no rígidos a fin de no incluir rigideces adicionales.
| Descripción |
Fx [N] |
Fy [N] |
Fz [N] |
Mx [Nm] |
My [Nm] |
Mz [Nm] |
|---|---|---|---|---|---|---|
| Fuerza de suspensión: Sobre las superficies de contacto de los rodamientos con la mangueta | 3300 | -3200 | 1500 | |||
| Peso del motor: En los 4 agujeros frontales | -300 | |||||
| Fuerza de frenado: En los 2 agujeros laterales | -3500 | |||||
| Par de la corona de transmisión: En el cilindro interior | -330 |
En la figura 3 y figura 4 se muestran respectivamente las cargas aplicadas y las restricciones de desplazamiento impuestas al modelo según el sistema de coordenadas del modelo geométrico.
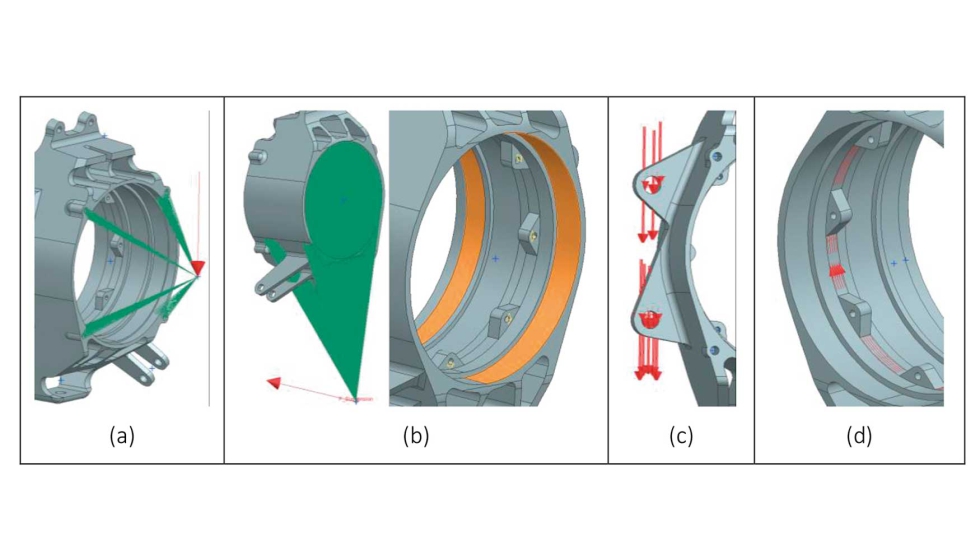
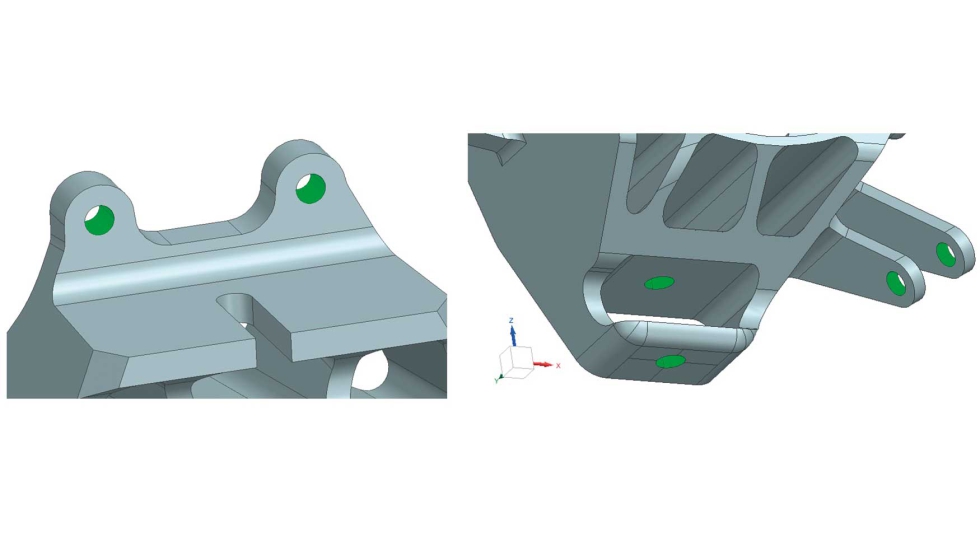
En la tabla 2 se muestran las propiedades mecánicas del material Al7075 T6 empleadas para cálculo estructural del modelo original (fabricado mediante mecanizado por arranque de viruta).
Con este valor de densidad la masa de la mangueta original es de 720 g.
| Propiedad | Valor |
|---|---|
| Densidad = | 2.770 kg/m³ |
| Módulo de elasticidad = | 71.000 MPa |
| Coeficiente de Poisson = | 0,33 |
| Resistencia a tracción = | 280 MPa |
| Tensión de rotura = | 310 MPa |
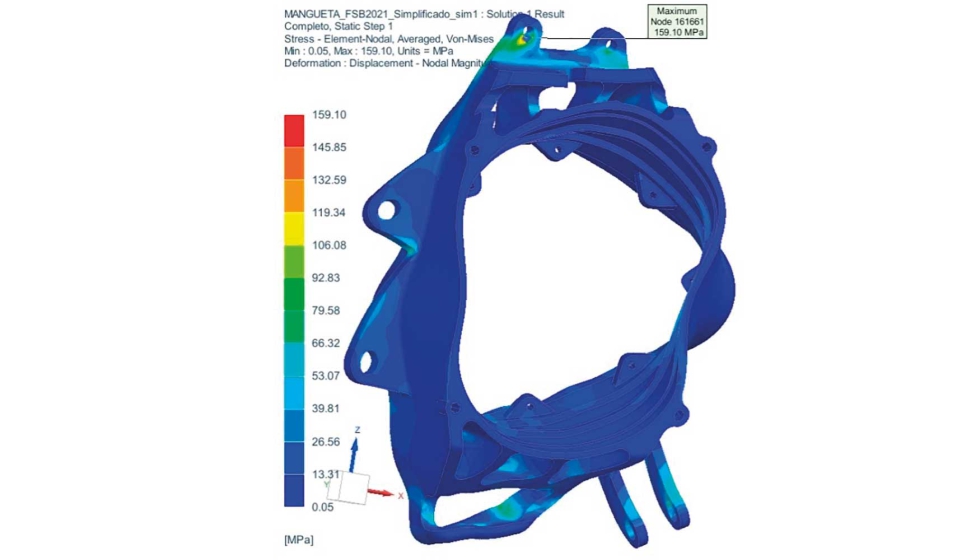
En la siguiente tabla 3 se muestran los valores de desplazamiento y de tensión nodales máximos de Von Mises para cada una de las cargas aplicadas, incluyendo la gravedad; como se puede apreciar, el efecto de la gravedad es muy pequeño en comparación al resto de las cargas, por lo que no se ha contemplado el efecto de esta carga en cálculo final.
A pesar de que, en la práctica real, todas estas fuerzas no se van a ejercer de manera conjunta, se ha optado por considerar como valores de referencia del estudio los valores de desplazamiento y tensión correspondientes al conjunto de cargas.
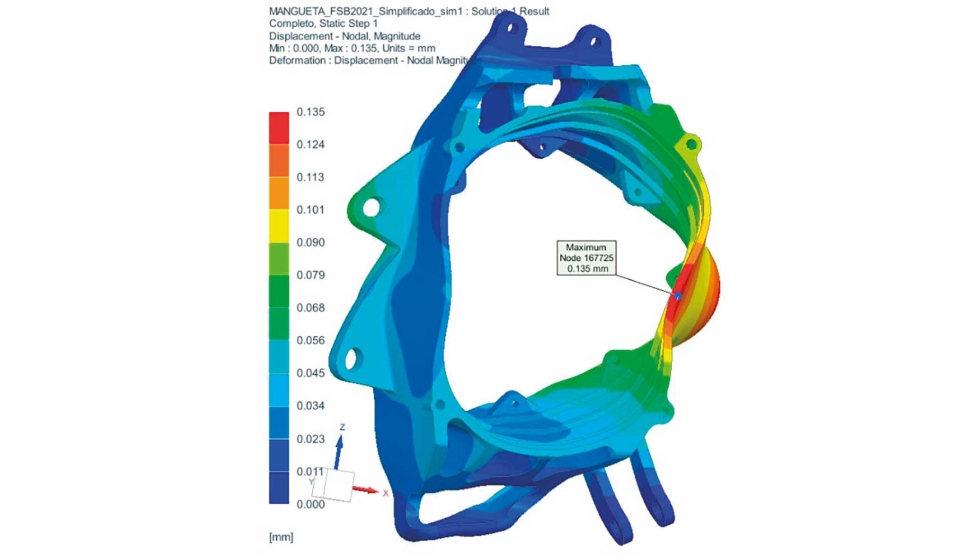
Por otra parte, en este estudio no se ha tenido en cuenta la rigidez que aportarían a la pieza los 2 rodamientos interiores que soportan la carga de la suspensión; sólo se ha tenido en cuenta la flexibilidad de la mangueta. A continuación, en las figuras 5 y 6 se muestran el mapa de desplazamientos y tensión Von Mises, respectivamente.
| Caso de carga | Desplazamiento [mm] | Tensión Von Mises [MPa] |
|---|---|---|
| Fuerza de suspensión | 0,135 | 130,9 |
| Peso del motor | 0,006 | 9.9 |
| Fuerza de frenado | 0,045 | 69,1 |
| Par de la corona de transmisión | 0,011 | 34,4 |
| (Gravedad) | 0.029 x 10-3 | 0,067 |
| TOTAL | 0,135 | 159,1 |
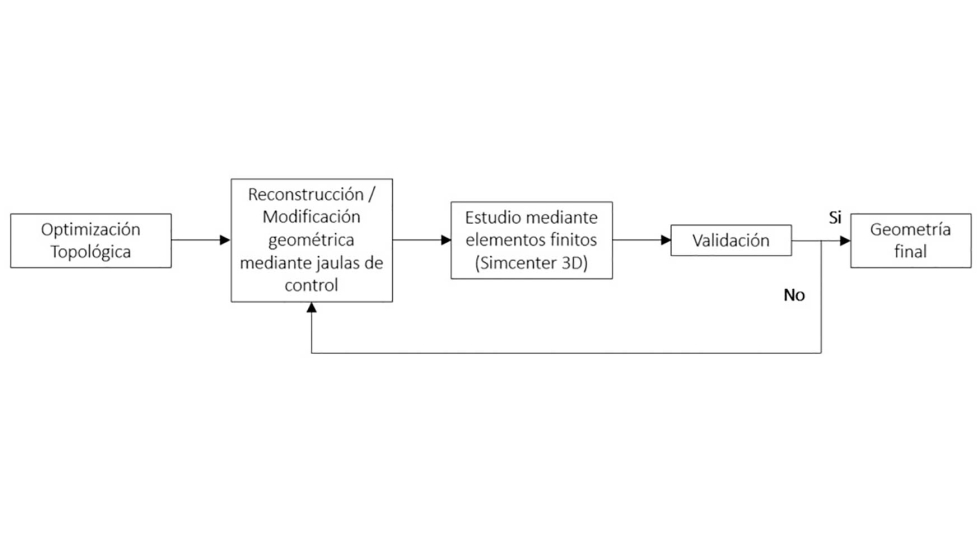
En el siguiente paso se ha realizado un estudio de optimización topológica con el módulo de Topology Optimization de NX. Para ello se han definido tanto el espacio de diseño como las Feature (o características) en las que se aplican restricciones de desplazamiento, cargas y otras restricciones geométricas impuestas por la propia funcionalidad de la pieza (ver figura 7). Se han realizado varios estudios, modificando el valor de masa objetivo y el nivel de resolución, hasta obtener un modelo optimizado que satisfaga geométricamente cada una de las funcionalidades antes referidas.

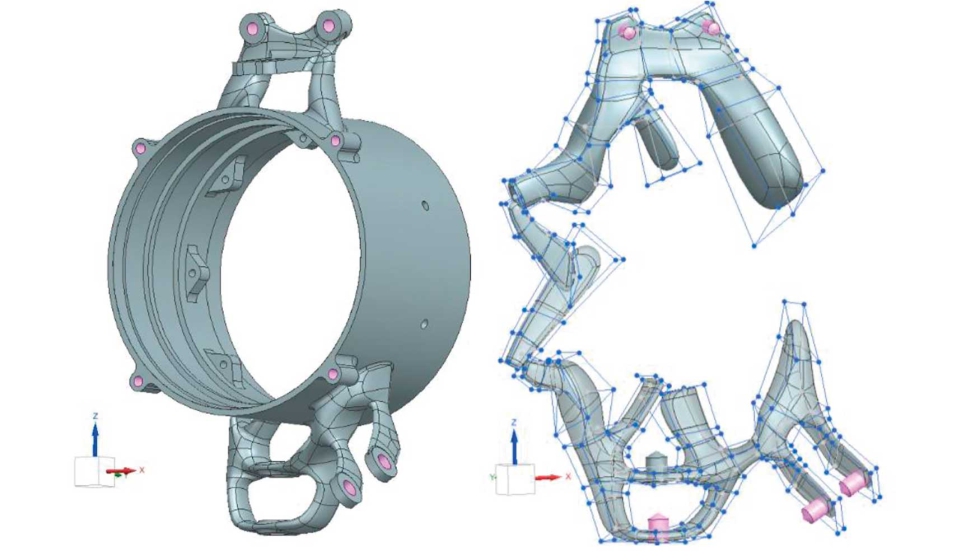
Tomando como referencia el modelo optimizado se ha realizado la reconstrucción geométrica a partir del modelo convergente de la pieza optimizada y se ha llevado a cabo el análisis estructural mediante el método de elementos finitos a fin de conocer el estado de deformación y tensional de la pieza; para modificar la geometría de la pieza se han manipulado los vértices, aristas y superficies de las jaulas que controlan la geometría del modelo optimizado (ver figura 9). Este proceso se ha llevado a cabo varias veces hasta haber validado el modelo teniendo en cuenta la resistencia a la tracción del material y los valores de referencia obtenidos con el modelo inicial (figura 8).
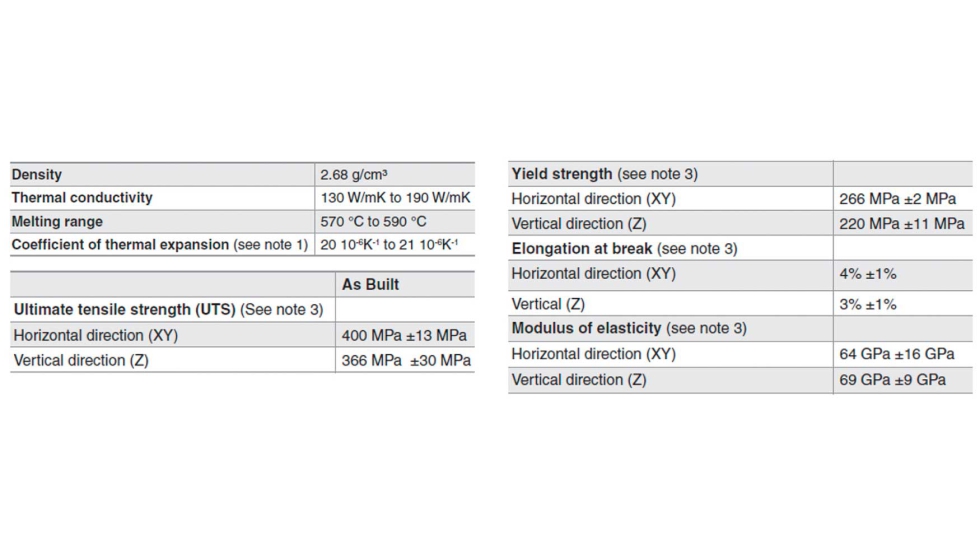
Teniendo en cuenta que la fabricación de la mangueta optimizada se llevará a cabo en la máquina de impresión 3D Renishaw AM250, tanto para la optimización topológica y como para el posterior análisis estructural mediante elementos finitos del modelo optimizado se han empleado las propiedades mecánicas que publica Renishaw para el material AlSi10Mg (tabla 4).
Aunque todavía, en esta fase del diseño, puede ser prematuro conocer cuál será la orientación de la pieza en el volumen de fabricación, en este caso se prevé que la pieza se posicionará con el eje de revolución central en posición vertical, es decir, con una de las caras frontales del cilindro principal en paralelo al sustrato, asignando a la dirección del eje de revolución del cilindro principal las propiedades del material correspondientes a la dirección Z de fabricación (tabla 4). No obstante, observando que los valores del módulo de elasticidad en el plano XY y dirección en Z son muy similares (64 y 69 GPa respectivamente), se ha optado por utilizar un material isotrópico con el valor más bajo.
A continuación, se muestran los resultados de desplazamiento y tensión Von Mises obtenidos en el modelo optimizado final.
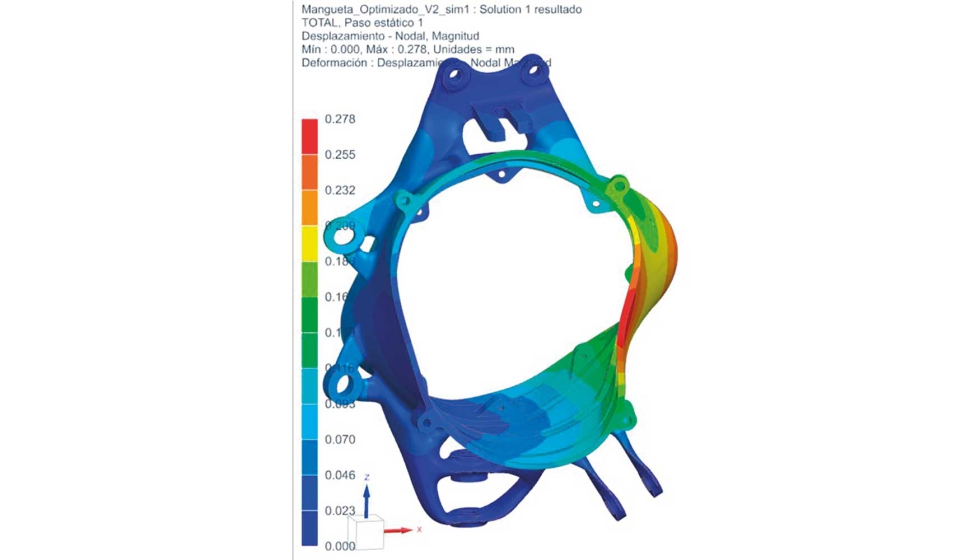

Si se compara el modelo optimizado con el modelo inicial (ver tabla 5), se obtiene una reducción del 27,5% en el peso de la pieza (194,7 g en cada una de las ruedas lo que equivale a 778,8 g en total) a costa de un incremento del 106 % en el desplazamiento y un incremento del 17,4 % en el valor máximo de la tensión Von Mises. En el caso del desplazamiento no se considera un incremento crítico debido a que la zona de desplazamiento máximo se produce en el cuerpo cilíndrico principal que en realidad está rigidizada con la presencia de los rodamientos y el sistema planetario que transmite el movimiento del motor eléctrico a las ruedas. En cuanto a la tensión, y teniendo en cuenta los valores mínimos de resistencia a la tracción para los materiales empleados (tabla 2 y tabla 4), se obtiene un factor de seguridad de 1,2 que podría no ser suficiente para un cálculo de fatiga.
No obstante, analizando el mapa de tensiones de la pieza de la figura 11, se observa que los valores máximos se producen en unas pocas zonas pequeñas muy localizadas, como bordes en ángulo recto. Estas zonas se pueden modificar geométricamente aplicando pequeños radios de acuerdo que minimicen las concentraciones de tensiones.
En este punto hay que incidir en que las geometrías de los cuerpos topológicamente optimizados resultan más complejas de mallar con una buena calidad de elementos en comparación a las geometrías mayoritariamente prismáticas de las piezas diseñadas para su fabricación mediante procesos convencionales.
| Caso de carga > TOTAL |
Masa [g] |
Desplazamiento [mm] |
Tensión Von Mises [MPa] |
|---|---|---|---|
| Modelo inicial | 720 | 0,135 | 159,1 (R.T. = 280; f.s. =1.76) |
| Modelo Optimizado | 525,3 | 0,278 | 186,8 (R.T. = 220; f.s. = 1.2) |
| Diferencia | ↓27,5% | ↑106% | ↑17,4% |
El siguiente paso ha consistido en analizar, en paralelo, la fabricación de la pieza mediante la tecnología LPBF de FA en la máquina de impresión 3D Renishaw AM250 y su posterior posproceso en un centro de mecanizado de 5 ejes. Este estudio ha permitido por una parte modificar la geometría en zonas concretas de la pieza a fin de reducir el número de soportes, y por otra parte, determinar la necesidad de algún utillaje específico o de geometría adicional para el amarre de la pieza en la bancada de la mesa. Adicionalmente, se ha añadido un sobreespesor de 1,5-2 mm en las superficies que requieren de un mecanizado. En la siguiente figura 12 se resumen las principales modificaciones geométricas aplicadas sobre la pieza.
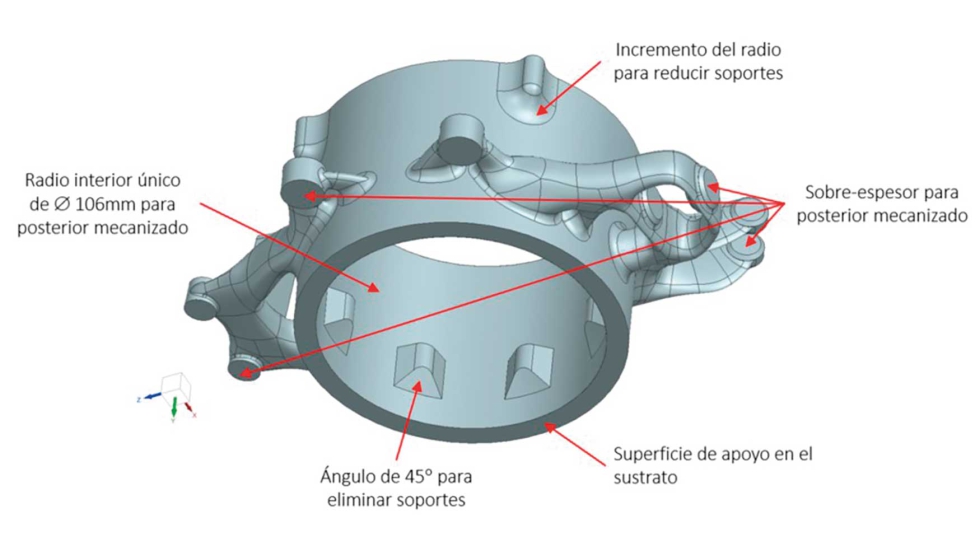
En cuanto al proceso de mecanizado se ha optado por mecanizar la pieza en 2 amarres, amarrando la pieza en el primer amarre por uno de los extremos del diámetro interior del cuerpo cilíndrico mediante unas garras interiores y en el segundo amarre por el extremo opuesto previamente mecanizado, garantizando la concentricidad de las 2 superficies de apoyo de los rodamientos. En la siguiente figura 13 se muestran las simulaciones de mecanizado CAM ejecutadas mediante el software de programación CAM PowerMill Ultimate 2022.
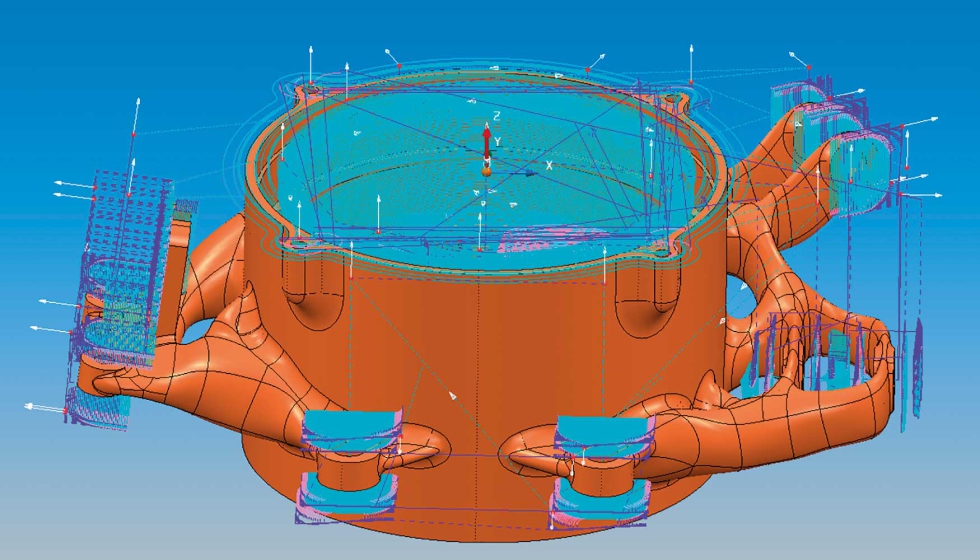
Para la creación de soportes se ha empleado el software Renishaw QuantAM 5.3. En la siguiente figura 14 se muestra la escena de fabricación de la mangueta mediante FA con los soportes correspondientes, los cuales deben de ser eliminados manualmente antes del proceso de mecanizado.
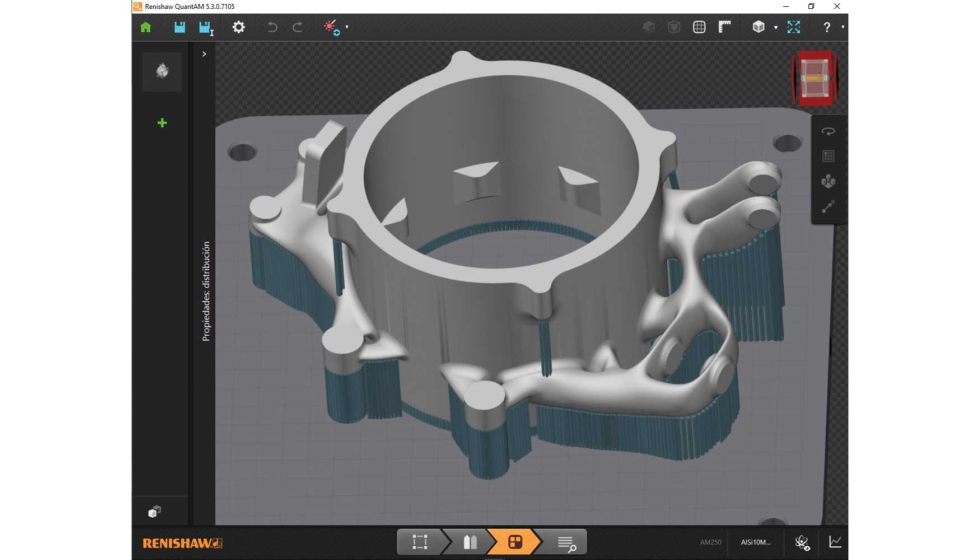
Fabricación de la mangueta mediante tecnología LPBF
Una vez concluida la fase de diseño, se ha procedido a la fabricación de la mangueta en la máquina de impresión 3D Renishaw AM250 con el material en polvo AlSi10Mg (ver figura 15). Después de la fabricación, y como primera fase de posprocesado, se han eliminado manualmente todos los soportes.

Antes de proceder al mecanizado, y con el objetivo de conocer las desviaciones geométricas producidas en la pieza en el proceso de fabricación mediante FA, se ha realizado una simulación mecánico-térmica del proceso mediante la operación Print3D del módulo de FA Inspire de Altair a la vez que se ha escaneado la pieza con un escáner de luz estructurada y precisión máxima de 50 µm (ver figura 16), con el fin de contrastar, por una parte, el comportamiento de la pieza en la simulación con la realidad, y por otra parte, cuantificar la magnitud de las desviaciones (en relación al modelo CAD mediante el PC-Demis) a fin de poder ajustar los sobreespesores aplicados en la pieza para su posterior mecanizado.

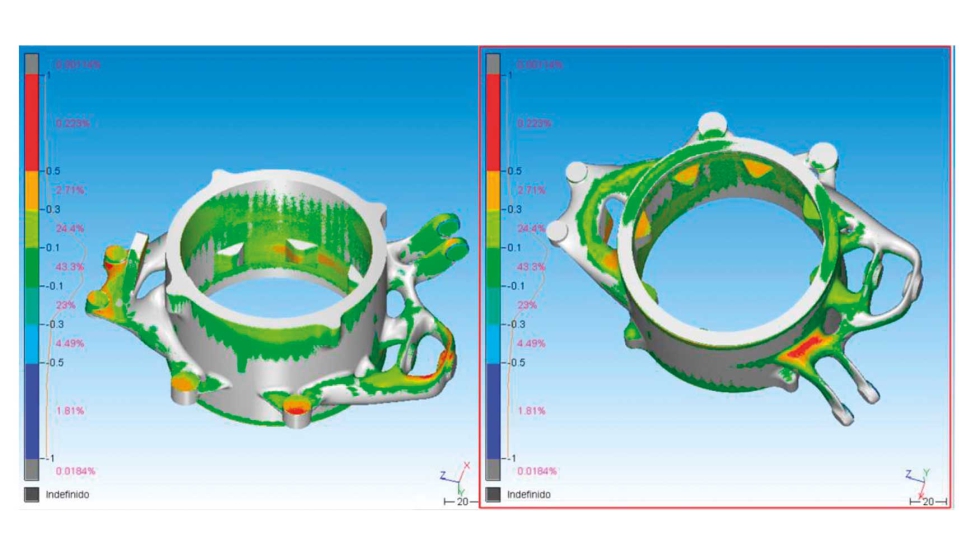
En la figura 17 se muestran las desviaciones geométricas de la pieza fabricada mediante FA y escaneada mediante escáner de luz estructurada (mapa de colores) en relación al diseño 3D de la pieza (pieza de color gris), siendo la imagen de la izquierda la que corresponde a la posición de fabricación con el eje Z de construcción en sentido vertical. En ella se aprecia que, en todas las geometrías con voladizos, es decir, todas las geometrías que requieren de soportes (ver figura 14), existe una deformación de toda esta geometría en dirección Z con desplazamientos que superan los 0,5 mm. A pesar de ello, el 43,3% del material se encuentra dentro de un margen de distorsión de +/- 0,1 mm y otro 47% en un margen de +/- 0.3mm; sólo el 7,1% está por encima de una tolerancia de +/-0,5 mm, quedando el 2,1% restante entre +/-0,5 y +/-1 mm.
Este estudio debe ayudar al ingeniero a tener en cuenta varios aspectos claves del proceso de diseño:
- El primero consiste en revisar el diseño de los soportes de forma que se incremente el volumen de material de soporte para facilitar la transferencia de calor generado en el proceso de fusión hacia el sustrato, evitando así los efectos de deformación de material debido a las concentraciones de calor.
- La calidad del escaneado es otro factor clave; al tratarse de una geometría con superficies curvadas (geometrías no-parametrizables), y en el caso de que existan tramos de superficie sin malla (debido por ejemplo a la dificultad del acceso con el escáner), resulta más difícil ejecutar la tarea de cierre de toda la malla haciendo uso de las herramientas que ofrecen los módulos de ingeniería inversa, dejando a menudo en manos del propio programa dicha labor de generación superficial. Esto puede provocar imprecisiones de malla que generan errores geométricos a la hora de compararlo con el modelo original.
- En este estudio no se han analizado los posibles tratamientos térmicos de relajación de tensiones a los que se puede someter esta pieza de aluminio, que permitiría reducir considerablemente las deformaciones.
- Una vez que se conocen los desplazamientos de material en cada zona, se puede determinar con mayor precisión el sobreespesor a asignar a cada zona de la pieza en función de la necesidad de mecanizado.
Finalmente se ha procedido a ejecutar la fase de post-proceso de mecanizado de la mangueta en el centro de mecanizado multiproceso Seaska de la marca Kondia (ver figura 18). Como se ha indicado anteriormente, todas las operaciones de mecanizado se han realizado en 2 amarres de pieza. Habiendo partido de una pieza en bruto de 844 g (sin contar los soportes) y con una masa de pieza final de 525,3 g, la ratio buy-to-fly de la mangueta mediante el proceso de FA es de 1,61 mientras que la pieza original fabricada por mecanizado (bruto de 205 x 190 x 110 mm³) tiene una ratio de 16,5 (masa del material en bruto de 11,87 kg y de la pieza final de 0,720 kg).

En la siguiente figura 19 se muestran varias imágenes con detalles de la pieza. El siguiente y último paso a ejecutar en el marco de este proyecto consiste en la verificación del montaje en el Monoplaza FSB2022 que a día de la publicación de este artículo no se ha llevado a cabo.

Análisis económico del proceso
Es por todos conocido que la integración de las tecnologías de FA resulta a menudo, sobre todo en lotes de fabricación medianos y grandes, más costoso en comparación a los procesos convencionales. En este proyecto no se ha cuantificado el coste total que ha supuesto la ejecución de cada una de las fases (actividades de diseño, fabricación mediante FA, posproceso de eliminación de soportes, definición de utillaje para el mecanizado y mecanizado como actividades principales) en comparación al mecanizado del modelo de referencia, pero se intuye que ha sido superior. En todos los proyectos en los que se decide integrar la FA, además de analizar el coste del proyecto mediante cualquiera de los métodos existentes en la literatura [7], [8] hay que buscar la ventaja estratégica o valor añadido que se le aporta a la pieza, y en este caso concreto es una reducción de peso del 27,5% en un componente que se encuentra ubicado junto a un componente que tiene su propia cinemática en relación al resto del vehículo, como es la rueda.
Conclusiones
Este estudio, desarrollado en el marco de una actividad formativa que se imparte en la Escuela Universitaria de Ingeniería Dual IMH-Campus, engloba, además del proceso de fabricación, todas las fases de diseño que requiere un proyecto de optimización topológica orientada a la fabricación mediante tecnologías de FA. A continuación, se resumen las conclusiones más importantes que se han obtenido:
- El diseño es una de las actividades más importantes dentro del desarrollo de nuevos productos o procesos de optimización; el resultado de la optimización topológica para la reducción de masa, la fabricación mediante FA y del ciclo de posprocesado por mecanizado dependen de ello.
- La herramienta de simulación de análisis estructural mediante elementos finitos es básica a fin de conocer el estado tensional de la geometría optimizada y de contrastar dichos resultados con los de la geometría inicial. Hay que resaltar que el proceso de mallado del cuerpo optimizado con múltiples superficies curvadas resulta algo más laborioso debido a que a menudo las superficies generadas presentan discontinuidades o cambios bruscos de geometría que dificultan una malla de calidad.
- Los softwares de simulación de los procesos de FA, en este caso particular la tecnología LPBF, son una herramienta muy útil para predecir las zonas críticas en las que pueden existir deformaciones debido a la falta de soportes.
- Como principal valor añadido de la integración de la FA en el proceso de fabricación de la mangueta, se ha conseguido reducir el peso en un 27,5%, lo que equivale a 778,8 g menos en total.
- En cuanto a los esfuerzos máximos en pieza, es obvio que a menor cantidad de material puedan generarse valores de tensión superiores. El principio de la optimización topológica consiste en eliminar material en zonas donde el nivel tensional es muy bajo, pero también hay zonas en las que se ha podido reducir la cantidad de material que soporta los esfuerzos, aumentando en este caso el nivel de tensión. Es por ello que el software de elementos finitos juega un papel importante, garantizando que no se superen los límites de resistencia del material, si es posible con un factor de seguridad.
El aspecto económico es otro de los estudios fundamentales a analizar, sobre todo si se trata de lotes de fabricación medianos o grandes. En sectores como el que se posiciona este proyecto, vehículos de competición y series unitarias, el aspecto económico puede pasar a un segundo plano, pero no por ello deja de ser importante; hay que valorar dicho coste frente a los beneficios que aporta el valor añadido.
Bibliografía
[1] R. Ranjan, R. Samant, and S. Anand, 'Integration of Design for Manufacturing Methods with Topology Optimization in Additive Manufacturing', J. Manuf. Sci. Eng. Trans. ASME, vol. 139, no. 6, pp. 1–14, 2017, doi: 10.1115/1.4035216.
[2] E. Dalpadulo, F. Gherardini, F. Pini, and F. Leali, 'Integration of topology optimisation and design variants selection for additive manufacturing-based systematic product redesign', Appl. Sci., vol. 10, no. 21, pp. 1–13, 2020, doi: 10.3390/app10217841.
[3] D. M. Nieto and D. M. Sánchez, 'Design for additive manufacturing: Tool review and a case study', Appl. Sci., vol. 11, no. 4, pp. 1–13, 2021, doi: 10.3390/app11041571.
[4] Francis Xavier Joseph, 'Design For Additive manufacturing - A Review', Int. J. Appl. Eng. Res., vol. 14 No. 14, no. Special issue, pp. 16–21, 2019.
[5] S. Li, Y. Xin, Y. Yu, and Y. Wang, 'Design for additive manufacturing from a force-flow perspective', Mater. Des., vol. 204, p. 109664, 2021, doi: 10.1016/j.matdes.2021.109664.
[6] S. Liu, Q. Li, J. Liu, W. Chen, and Y. Zhang, 'A Realization Method for Transforming a Topology Optimization Design into Additive Manufacturing Structures', Engineering, vol. 4, no. 2, pp. 277–285, 2018, doi: 10.1016/j.eng.2017.09.002.
[7] G. Cardeal, D. Sequeira, J. Mendonça, M. Leite, and I. Ribeiro, 'Additive manufacturing in the process industry: A process-based cost model to study life cycle cost and the viability of additive manufacturing spare parts.', in Procedia CIRP, 2021, vol. 98, pp. 211–216. doi: 10.1016/j.procir.2021.01.032.
[8] G. Costabile, M. Fera, F. Fruggiero, A. Lambiase, and D. Pham, 'Cost models of additive manufacturing: A literature review', Int. J. Ind. Eng. Comput., vol. 8, no. 2, pp. 263–282, Apr. 2016, doi: 10.5267/j.ijiec.2016.9.001.














