Predicción de distorsiones en piezas esbeltas mecanizadas para el sector aeronáutico
Durante el mecanizado de piezas esbeltas y/o de paredes delgadas de aluminio típicas del sector aeronáutico, la complejidad del proceso interacciona con la necesidad de obtener elevadas tolerancias dimensionales junto con excelentes propiedades mecánicas de la pieza final. Un problema habitual que presenta este tipo de piezas es la aparición de distorsiones no despreciables una vez que son mecanizadas. Esto se debe, principalmente, a que las piezas no están perfectamente estabilizadas y presentan de partida un nivel importante de tensiones residuales. Una vez que se elimina el material y la pieza se retira de su sistema de amarre, las tensiones tienden a un nuevo estado de equilibrio induciendo un cambio geométrico en la pieza.
1. Introducción
La fabricación de componentes estructurales para el sector aeronáutico presenta un número considerable de dificultades. Las necesidades en cuanto a la maximización de las capacidades de carga, junto con la minimización del consumo energético en sistemas de transporte aéreo, empuja al uso de materiales de elevadas propiedades mecánicas y pesos específicos reducidos dentro del sector aeronáutico. De manera análoga, el diseño de componentes estructurales tiende hacia estructuras nervadas de gran esbeltez (figura 1), lo que optimiza la capacidad de carga de los componentes para un peso de componente dado.

De esta manera, este tipo de piezas presentan rigurosos requisitos en cuanto a integridad estructural y superficial del componente, tolerancias dimensionales o acabados superficiales; puntos que permiten asegurar el correcto comportamiento de estos elemento estructurales durante su vida útil.
Debido a las necesidades en cuanto a materiales y diseño existentes para componentes de aviación, es posible encontrar ciertas dificultades durante su fabricación, pudiendo generar defectos que hagan que la pieza fabricada no cumpla los estrictos requerimientos definidos para ella. Aspectos como inestabilidad es dinámicas durante el proceso de mecanizado, distorsiones en pieza debido a la presencia de tensiones residuales volumétricas, deformaciones térmicas e incluso alteraciones microestructurales debido al calor generado durante el proceso de corte o la generación de capas con elevadas tensiones residuales y deformaciones mecánicas en superficie han sido ampliamente reportados [1,2].
En el caso específico de componentes estructurales para aviación de gran esbeltez, en los que llega a eliminarse hasta un 90-95% de material, los principales problemas de fabricación están relacionados con la aparición de distorsiones en las piezas mecanizadas debido al estado tensional presente en los brutos antes del proceso de mecaniza o [3,4]. Ejemplos de este tipo de fallos pueden observarse en la figura 2.

Por todo ello, la correcta planificación en cuanto a la estrategia y diferentes fases de mecanizado, así como la selección de la zona más adecuada para la obtención del componente mecanizado resultan de gran importancia a la hora de obtener un componente con el mínimo de distorsiones de manera que satisfaga los requerimientos especificados para él [6]. A pesar de ello, las estrategias resultantes suelen mostrar gran cantidad de cambios de atadas, junto con un volumen de material reducido en cada una de estas atadas. Todo ello lleva a grandes tiempos de procesado para la obtención de un componente con mínimas distorsiones.
El presente trabajo tiene como objetivo el desarrollo de un modelo de cálculo que, por un lado, permita identificar el estado tensional de un bruto de mecanizado de manera sencilla. Por otro, deberá ser capaz de calcular el estado final de una pieza tras un proceso de mecanizado. Dichos desarrollos servirán como base para una herramienta general que permita definir una estrategia de mecanizado que, en función del estado inicial del material base, minimice la distorsión final en componentes mecanizados, así como resulte en tiempos de procesado competitivos para componentes de gran esbeltez.
2. Caracterización del estado del material
Con intención de desarrollar una herramienta que permita estimar el estado o distorsión final de una pieza mecanizada, se han realizado un número de ensayos experimentales para la caracterización del estado del material bruto a mecanizar. El material seleccionado ha sido una aleación de aluminio Al 7050-T651, habitual en componentes estructurales aeronáuticos. Dicha aleación presenta un estado de envejecido por precipitación tras un proceso de tratamiento térmico de solubilización y posterior estirado para la liberación de tensiones.
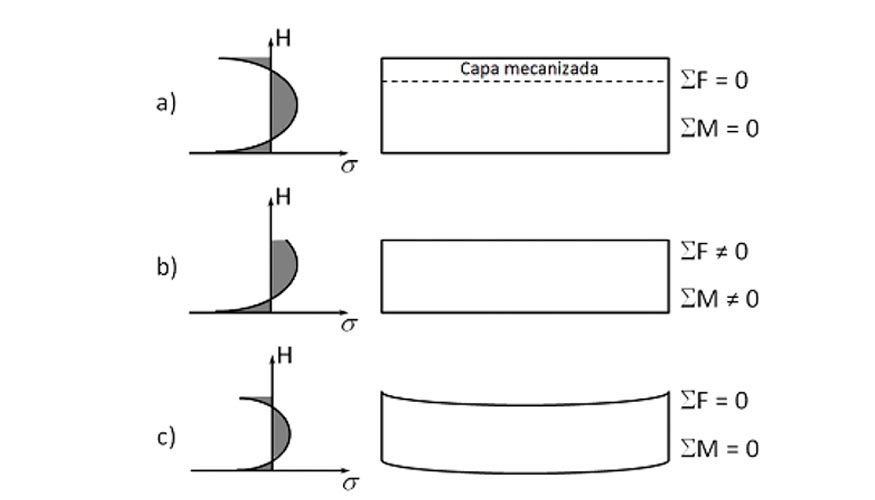
Para llevar a cabo la caracterización del estado tensional, se ha llevado a cabo un proceso de eliminación sucesiva de capas de material en las placas de aluminio y la posterior medición de la curvatura alcanzada por éstas. Cuando se elimina una capa de material en uno de los lados de una placa plana que contiene tensiones residuales, se altera el equilibrio de tensiones en la placa de manera que ésta de deforma tras liberar las fuerzas de amarre para alcanzar un nuevo estado de equilibrio (figura 3). La curvatura alcanzada por la placa depende de la distribución de tensiones originalmente presente en la capa eliminada, así como de las propiedades elásticas de del resto de la placa. De esta manera, obteniendo mediciones de la curvatura alcanzada por la placa tras la eliminación sucesiva de varias capas de material, es posible calcular el estado tensional originalmente presente en la placa empleando la teoría de vigas de Euler-Bernoulli [7-11].
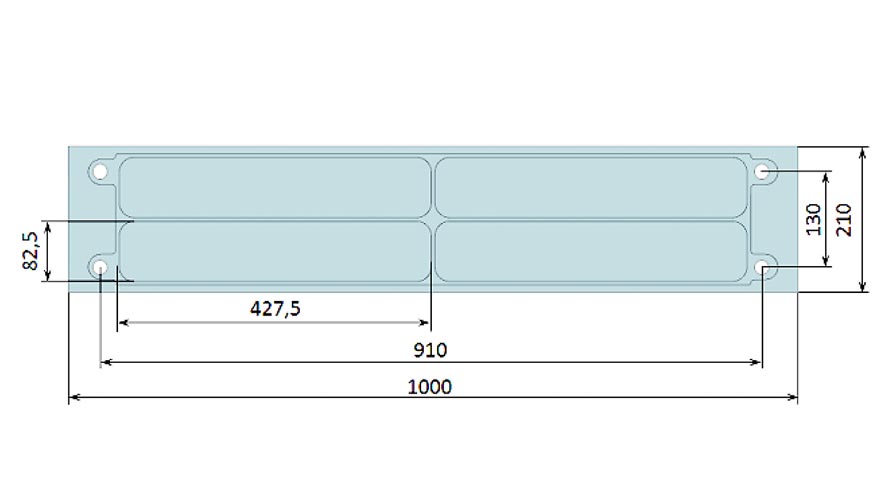
En el caso de estos ensayos, en lugar de realizar ensayos de pelado completo se ha decidido mecanizar una geometría que mostrara una estructura nervada similar a los componentes estructurales aeronáuticos. De esta manera, partiendo de brutos de aluminio de 1.000 x 210 x 30 mm, se han mecanizado 4 cajeras de 82,5 x 427,5 mm y 28 mm de profundidad, manteniendo nervios de 5 m de espesor entre cajeras. En la figura 4 puede observarse una imagen en planta de la probeta con las diferentes dimensiones, así como el bruto de partida. Los mecanizados se han llevado a cabo en una fresadora Soraluce SV-6000, empleando un plato de fresado tórico de 40 mm de diámetro con 3 placas XDHX 190404 FR-27P de Ceratizit. La tabla 1 muestra los diferentes parámetros de corte empleados durante los mecanizados.

Las cajeras se han mecanizado en 28 pasadas de 1 mm de profundidad, habiéndose liberad o las fuerzas de amarre tras cada pasada de 1 mm para realizar las mediciones de curvatura de las placas. La figura 5 muestra una imagen de la medición en máquina de la curvatura de las piezas empleando un indicador analógico sujeto al cabezal de la fresadora.

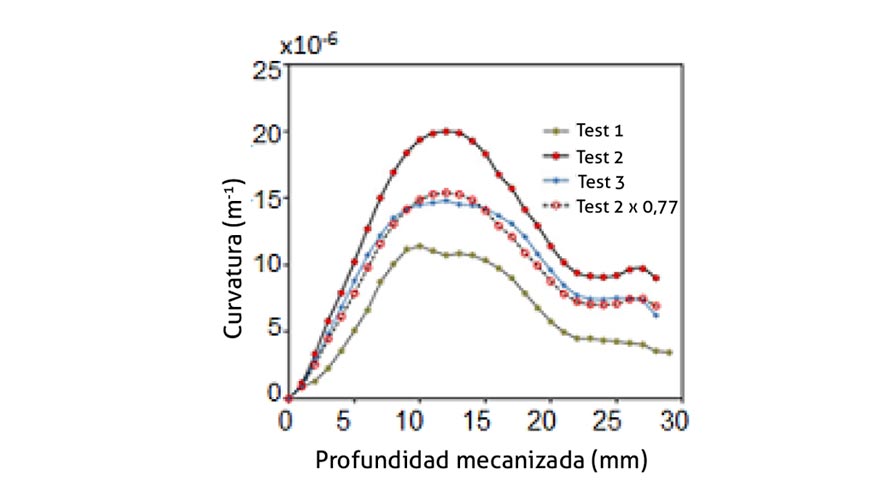
La figura 6 muestra las curvas correspondientes a la evolución de la curvatura obtenida para cada una de las placas analizadas. Puede observarse cómo la evolución de la curvatura obtenida para cada una de las placas ensayadas difiere. A pesar de ello, la forma de la curva para estas evoluciones es análoga, resultando posible definir una relación de múltiplos entre ellas. De esta manera, además de la evolución de la curvatura para las tres placas analizadas, la figura 6 muestra también la curva del ensayo 2 multiplicada por un factor de 0,77. Como puede observarse, esta curva se corresponde de buen acuerdo con la curva obtenida para el ensayo 3.
3. Desarrollo de modelo de tensiones y distorsiones
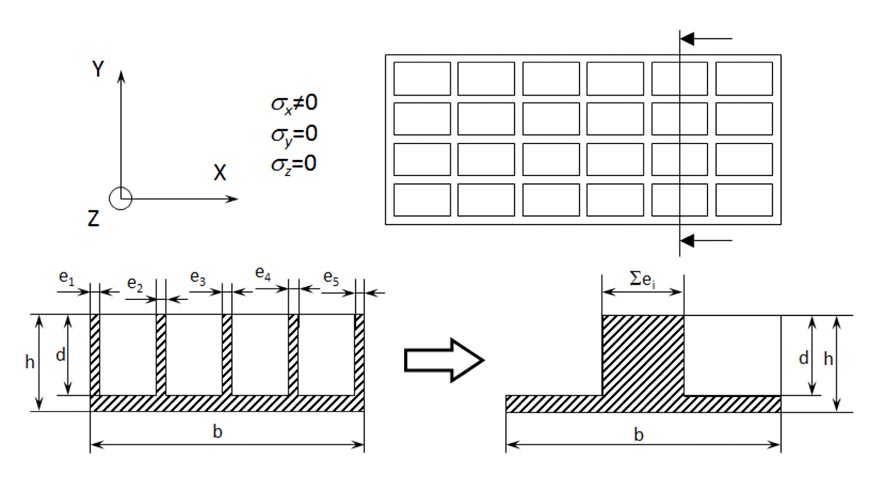
A la hora de plantear diferentes posibilidades para la construcción del modelo, la principal solución observada en trabajos de bibliografía se basa en el empleo del método de los elementos finitos (MEF) para realizar los cálculos de distorsiones en las piezas mecanizadas [12-15]. A pesar de ello, dado que se desea desarrollar una herramienta ágil que permita su uso de manera sencilla en ambientes industriales, se ha optado por su implementación mediante un modelo analítico a través del software MatLab. Mientras que un modelo analítico no es capaz de representar un caso de estudio tan en detalle como un modelo desarrollado mediante una herramienta MEF, permite una gran agilidad para modificar la geometría o condiciones iniciales de cálculo, así como unos requisitos considerablemente inferiores a los normalmente requeridos para programas de cálculo en base al MEF. Así, con intención de generar una herramienta que permita calcular tanto el estado tensional de las capas mecanizadas como la distorsión resultante de un proceso de mecanizado llevado a cabo sobre un bruto con tensiones residuales, se ha desarrollado un modelo de cálculo en base a los métodos expuestos en [7-11]. Para ello se han definido una serie de hipótesis en base a las observaciones realizadas durante los ensayos de pelado para la medición de la curvatura en las placas de aluminio. Por un lado, se ha observado que la curvatura es muy uniforme en la dirección longitudinal de la placa mecanizada, indicando una distribución de tensiones homogénea a lo largo de ésta, además de que el efecto de los nervios transversales de la pieza sobre la deformación final es despreciable. Por otro lado, la deformación alcanzada en la dirección transversal es prácticamente nula, habiéndose decidido desestimar el efecto de las tensiones en la dirección transversal dentro del modelo de distorsiones. En el caso de la dirección de profundidad, las tensiones han sido desestimadas también.
Gracias a que se desprecian las componentes de tensión en las direcciones transversal y en profundidad (direcciones Y y Z en la figura 7), así como la aportación de los nervios transversales al comportamiento a flexión del componente mecanizado; es posible representar el comportamiento a flexión de un componente nervado de geometría estándar mediante únicamente una sección transversal de dicho componente. Más aún, es posible reducir la complejidad de esta sección empleando una sección equivalente, asimilando las secciones de los diferentes nervios longitudinales a un único nervio ‘genérico’ que englobe el comportamiento a flexión de los diferentes nervios reales. Este procedimiento de reducción desde la geometría inicial hasta la geometría simplificada de cálculo puede observarse de manera esquemática en la figura 7. De esta manera, es posible definir un modelo de cálculo sencillo con la capacidad de representar virtualmente un gran número de geometrías reales.
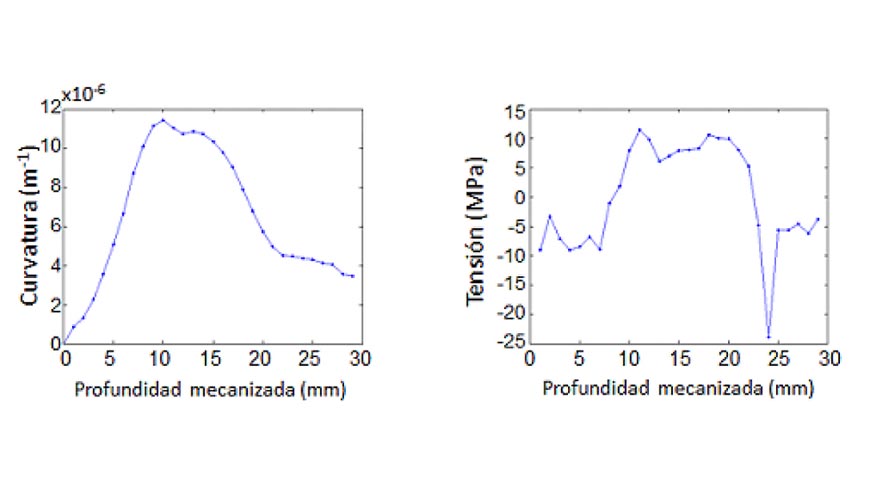
En base a las hipótesis y simplificaciones expuestas, se ha desarrollado un modelo de cálculo que permite obtener los resultados de tensiones a partir de los valores de curvatura obtenidos en los ensayos experimentales. Este modelo de tensiones ha sido empleado para el cálculo de los perfiles de tensiones residuales originalmente presentes en las placas mecanizadas. En la figura 7 pueden observarse los resultados de tensiones calculados para el ensayo 1 junto con la evolución de curvatura medida en dicho ensayo. Los valores de tensiones alcanzados por los diferentes ensayos muestran un buen acuerdo con los valores observados en bibliografía [5], si bien pudiera haberse esperado que los resultados de tensiones fueran simétricos con respecto a la línea media de la pieza.
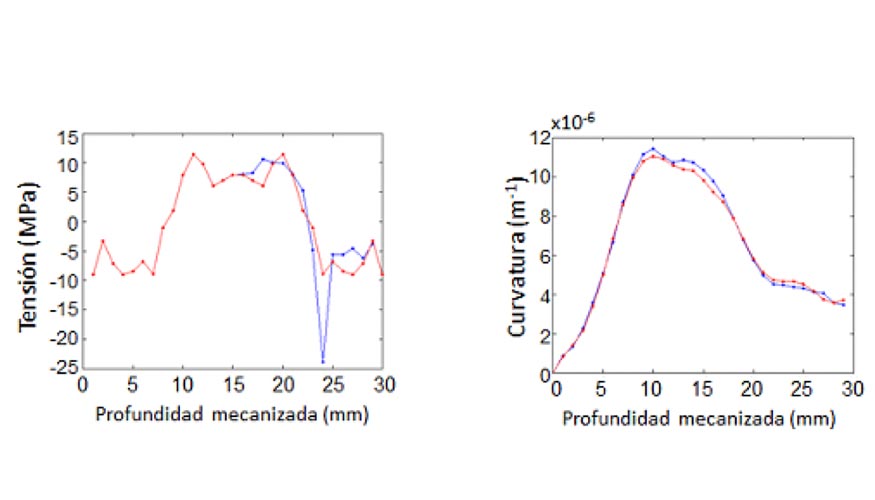
Una vez desarrollado el modelo de cálculo de tensiones a partir de las curvaturas observadas en los ensayos experimentales, se ha llevado a cabo la implementación de un modelo inverso que permita calcular las distorsiones finales en piezas mecanizadas a partir de un estado inicial de tensiones residuales. Debe tenerse en cuenta que en los ensayos de mecanizado realizados, no se ha llevado a cabo el mecanizado de las probetas en su totalidad (30 mm), si no que las cajeras se han mecanizado hasta una profundidad de 28 mm. Por ello, con intención de permitir disponer de valores de tensiones en toda la profundidad de las placas a mecanizar, se ha llevado a cabo una simetrización de las tensiones obtenidas de los ensayos experimentales con respecto a la línea media de la pieza mecanizada. Dado que la zona de la que no se disponen resultados de tensiones es la inferior de la pieza, los valores de tensiones empleado para la simetrización han sido los correspondientes a la mitad superior de las piezas mecanizadas. Una vez definida una distribución de tensiones simétrica para toda la profundidad de la pieza mecanizada, se ha llevado a cabo una simulación de los ensayos experimentales de caracterización realizados, obteniéndose valores de curvatura en comparación a los originalmente medidos en los ensayos experimentales. La figura 9 muestra de manera conjunta la distribución de tensiones residuales obtenida de los ensayos experimentales y la distribución simétrica definida para los cálculos de simulación, así como los resultados de curvaturas obtenidos de dichas simulaciones en comparación a los resultados de curvatura iniciales obtenidos en los ensayos experimentales. Como puede observarse, a pesar de encontrar desviaciones entre los valores de curvatura calculados mediante la distribución de tensiones simétrica y los inicialmente medidos en ensayos experimentales, las desviaciones obtenidas son inferiores al 5% en el caso de la curvatura final.
4. Validación de comportamiento del modelo
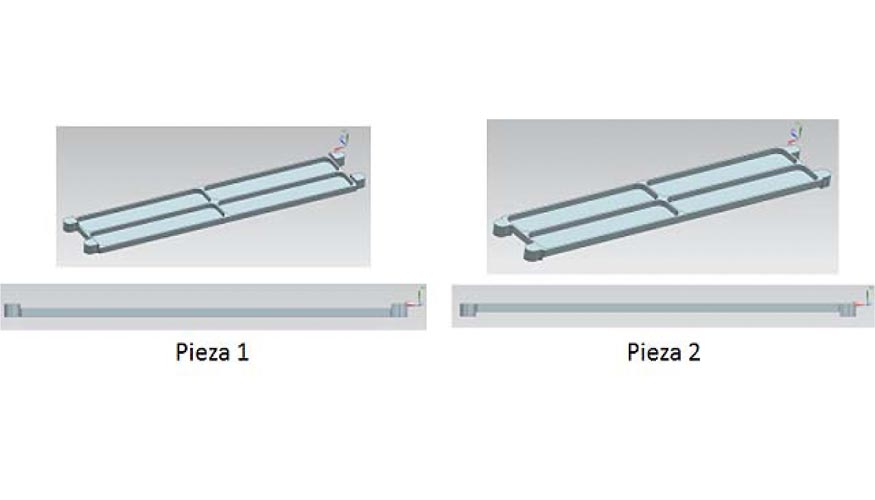
Con intención de evaluar la capacidad del modelo de distorsiones para el cálculo del estado de placas tras procesos de mecanizado, se han llevado a cabo el mecanizado de dos piezas de geometría análoga que pudieran mostrar curvaturas finales considerablemente diferentes. Para ello, se ha decidido mecanizar una geometría en planta idéntica a la empleada para las probetas de los ensayos experimentales de caracterización (figura 4), pero se ha modificado su altura, así como la profundidad de las cajeras. En el caso de estas piezas, su altura es de 20 mm y la profundidad de las cajeras se ha definido en 17 mm. De esta manera, dado que los brutos de mecanizado muestran una altura de 30 mm, es posible obtener estas piezas de diferentes zonas de la pieza en bruto. La figura 10 muestra este punto, de manera que la pieza 1 se ha obtenido de la parte ‘inferior’ del bruto, mientras que la pieza 2 se ha obtenido de la parte ‘superior’.
Durante los ensayos de caracterización de material mostrados en el punto 2, se ha observado que diferentes brutos de mecanizado muestran comportamientos diferentes entre sí, aunque pueda definirse un factor o múltiplo entre los comportamientos observados (figura 5). De esta manera, antes de proceder al mecanizado completo de las piezas de validación, se ha decidido plantear una fase preliminar de caracterización de los brutos de los que se obtendrán estas piezas; de manera que los datos de entrada para el cálculo de las curvaturas sea representativo del estado real de los brutos de los que vayan a obtenerse estas piezas. Para ello, se realizarán ensayos similares a los expuestos en el punto 2 pero alcanzando una profundidad de cajeras de 7 mm, lo que permitirá estimar el estado tensional de la placa a mecanizar en comparación a los resultados completos obtenidos en los ensayos de caracterización. Así, las fases de mecanizado empleadas para cada pieza pueden observarse en la tabla 2.
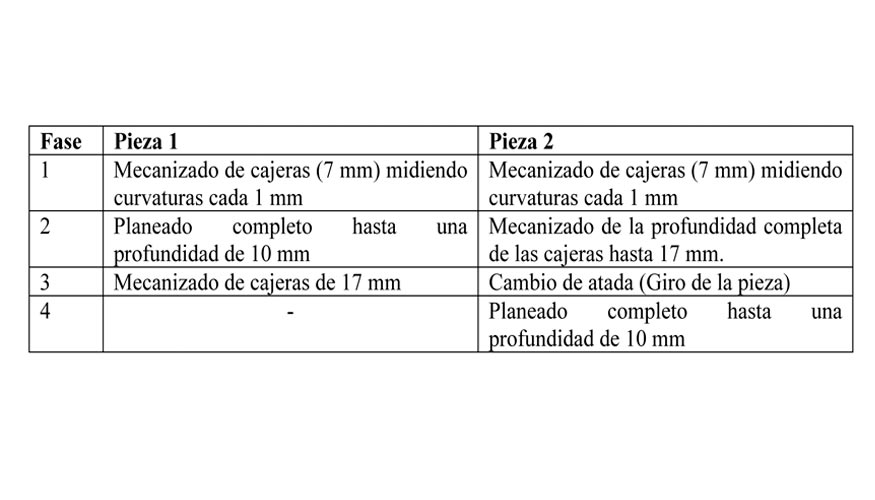
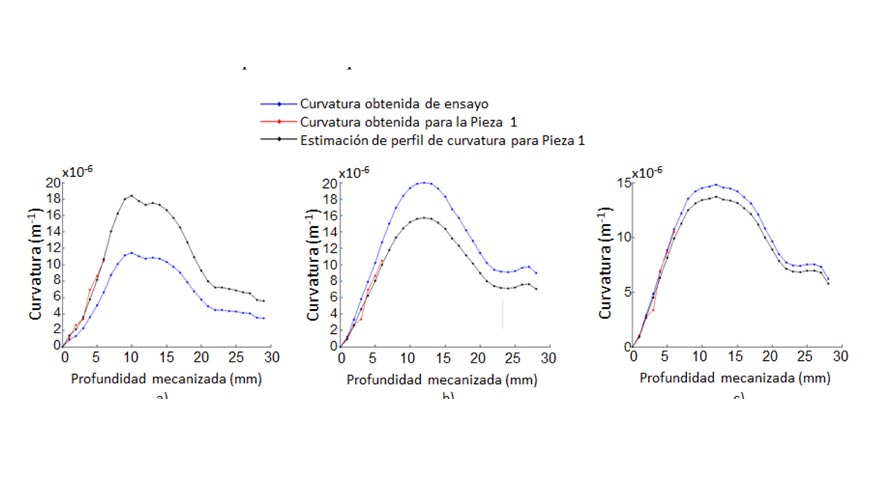
Una vez las dos piezas de validación han sido mecanizadas por completo, la curvatura alcanzada por cada una de ellas tras la liberación de las fuerzas de amarre ha sido medida de manera similar a lo expuesto dentro del punto 2. A continuación, se ha llevado a cabo la simulación de los mecanizados de ambas piezas mediante el modelo de distorsiones desarrollado dentro del punto 3. Para la estimación de del estado tensional inicial de las piezas mecanizadas, se parte de los resultados de curvatura obtenidos de la fase 1 para ambas piezas. Dichos datos se comparan con los datos de curvatura obtenidos para los diferentes ensayos de caracterización y, definiendo un factor o múltiplo para estos primeros 7 puntos, se estima el perfil completo de curvaturas para el componente a mecanizar (figura 11). De esta manera, en base a estas curvaturas estimadas en comparación a los resultados experimentales, es posible definir una distribución de tensiones dada para el componente a mecanizar.
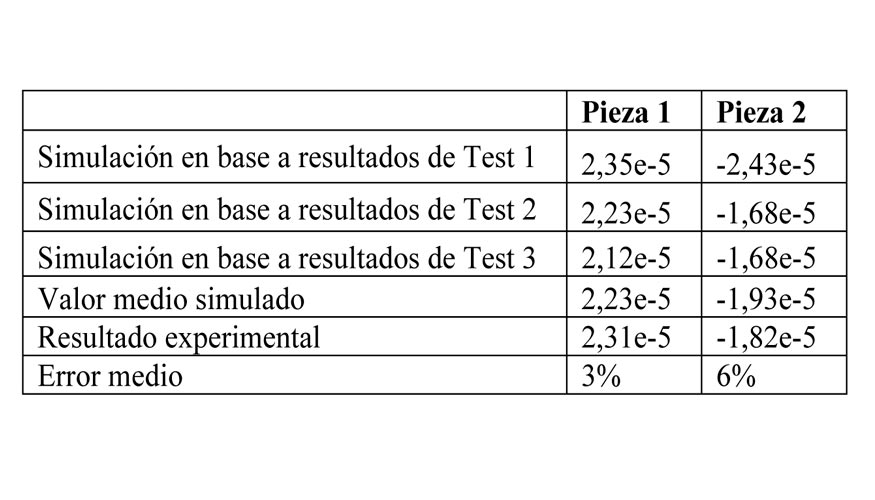
Una vez definidos unos estados de tensiones residuales para las piezas ensayadas, se ha llevado a cabo la simulación del proceso de mecanizado expuesto en la Tabla 2 para ambas piezas de validación. Dado que se disponían resultados de tres ensayos experimentales previos, se han realizado las simulaciones para los perfiles de tensiones correspondientes a cada uno de estos ensayos. De esta manera, se han obtenido 3 resultados diferentes para la simulación de cada pieza de validación, cada uno correspondiente a los datos iniciales obtenidos de cada ensayo de caracterización. La tabla 3 muestra estos resultados, así como el valor medio de las simulaciones realizadas, en comparación a los resultados de curvatura reales medidos de ambas piezas de validación. Como puede observarse, tomando cada uno de los resultados de simulación obtenidos, se observan diferencias considerables en comparación a los resultados experimentales de curvaturas obtenidos de ambas piezas de validación. A pesar de ello, tomando los valores medios de las 3 simulaciones, los resultados de curvatura calculados para ambas piezas de validación quedan en buen acuerdo con los medidos en las piezas mecanizadas, siendo posible estimar la distorsión final de piezas mecanizadas mediante el método de caracterización y modelo de distorsiones expuesto en el presente trabajo.
5. Conclusiones
Del análisis de los resultados expuestos pueden extraerse las siguientes conclusiones:
- A pesar de presentar la misma composición, tratamiento térmico y procedencia, diferentes placas de material pueden mostrar estados tensionales diferentes.
- Mientras que los valores de tensiones puedan resultar diferentes, es posible definir una familia tipo para las curvas de evolución de la curvatura de pieza.
- Dado el comportamiento observado en los ensayos de caracterización, ha sido posible desarrollar un modelo analítico sencillo para el cálculo de distorsiones en las piezas mecanizadas.
- El modelo de distorsiones desarrollado permite calcular el proceso de mecanizado de manera rápida y sencilla, resultando idóneo para su aplicación en estrategias de reducción de distorsiones en componentes mecanizados.
- El empleo de las curvaturas para estimar el estado de la pieza a mecanizar en función de ensayos experimentales previos, permite calcular el valor final de curvatura a tomar por un componente mecanizado con un buen grado de acierto.
Agradecimientos
Este trabajo ha sido parcialmente realizado dentro del proyecto INTEFIX (FP7-2013-NMP-ICT-FOF) financiado por la CE dentro del FP7. Los autores agradecen también al departamento de Industria, Comercio y Turismo del Gobierno Vasco el apoyo financiero otorgado al proyecto Estrateus a través del programa Etortek.
Bibliografía
[1] Brinksmeier E., Sölter J. 2009. Prediction of shape deviations in machining. CIRP Annals – Manufacturing Technology Vol. 58, pp. 507-510.
[2] Jawahir I.S., Brinksmeier E., M’Saoubi M., Aspinwall D.K., Outeiro J.C., Meyer D., Umbrello D., Jayal A.D. Surface integrity in material removal processes: Recent advances. CIRP Annals – Manufacturing Technology Vol. 60, pp. 603-626.
[3] Sim, W. 2010. Challenges of residual stresses and part distortion in the civil airframe industry, International Journal of Microstructure and Material Properties, Vol. 5, n. 4-5, pp.446-455.
[4] Chatelain J. F., Lalonde J. F., Tahan A. S. 2012. Effect of Residual Stresses Embedded within Workpieces on the Distortion of Parts after Machining. International Journal of Mechanics Vol. 1, pp. 43-51.
[5] Prime M. B., Hill M. R. 2002. Residual stress, stress relief, and inhomogeneity in aluminum plate. Scripta Materiala Vol. 46, pp. 77-82.
[6] Chantzis D., Van-der-Veen S., Zettler J., Sim W.M. 2013. An industrial workflow to minimise part distortion for machining of large monolithic components in aerospace industry. Procedia CIRP Vol. 8 (14th CIRP Conference on Modeling of Machining Operations), pp. 281-286.
[7] Treuting R.G., Read W.T. 1951. A Mechanical Determination of Biaxial Residual Stress in Sheet Materials. Journal of Applied Physics Vol. 22, n. 2, pp. 130-134.
[8] Brinksmeier E., Cammet J.T., König W., Leskovar P., Peters J., Tönshoff H.K. 1982. Residual stresses – Measurement and Causes in Machining Processes. CIRP Annals – Manufacturing Technology Vol. 31, n. 2, pp. 491-510.
[9] Ruud C., Measurement of residual stresses, Totten G., Howes M., Inoue T.. 2002. Handbook of residual Stress and Deformation of Steel, ASM International, pp. 99-117.
[10] Kandil F.A., Lord J.D., Fry A.T., Grant P.V. 2003. A Review of Residual Stress Measurement Methods – A guide to technical selection. NPL Materials Centre Queens Road Teddington, Middlesex.
[11] Dreier D., Denkena B. 2014. Determination of Residual Stresses in Plate Material by Layer Removal with Machine-integrated Measurement. Procedia CIRP Vol. 24 (New Production Technologies in Aerospace Industry - 5th Machining Innovations Conference MIC 2014), pp. 103-107.
[12] Wang Z., Chen W., Zhang Y., Chen Z., Liu Q. 2005. Study on the Machining Distortion of Thin-walled Part Caused by Redistribution of Residual Stress. Chinese Journal of Aeronautics Vol. 18 n. 2, pp. 175-179.
[13] Guo H., Zuo D. W., Wu H. B., Xu F., Tong Q. G. 2009. Prediction on milling distortion for aero-multi-frame parts. Materials Science and Engineering A Vol. 499, pp. 230-233.
[14] Zhongyi M., Yunqiao W. 2010. Analyzing Distortion of Aircraft Structural Part in NC Machining Based on FEM Simulation. Proceedings of 2010 International Conference on Mechanical and Electrical Technology (ICMET 2010)
[15] Chen J. 2012. Study on Machining Distortion of Residual Stress Release. Advanced Materials Research Vol. 426, pp 143-146.