Comportamiento de la capa de transferencia (colchón de reparto) y su influencia en el cálculo de losas y soleras

Departamento Técnico de Menard27/10/2015

Este documento constituye la segunda parte del artículo ‘Breve descripción de diferencias y analogías e introducción a la metodología de diseño del colchón de reparto (LTP) de las inclusiones rígidas’, publicado en octubré14 (nº 237). Un tratamiento por medio de inclusiones consiste en una mejora de la masa del terreno por medio de elementos cuya rigidez es mucho mayor que aquella del suelo que las contiene. Existen principalmente dos tipos de inclusiones: inclusiones flexibles constituidas por un material granular (columnas de grava) e inclusiones rígidas, constituidas por un material cementante con una puesta en obra con o sin presión (columnas de cemento vibrocompactadas, columnas de modulo controlado, columnas de soil mixing…).

Partiendo de la base de que el principio de ambos tipos de inclusiones es similar (es decir, la mejora en general de las características de la masa del terreno de cimentación), se tiene sin embargo que el mecanismo de transferencia de carga es radicalmente diferente en cada tipo de técnica. Por tanto, la metodología de diseño aplicable es específica para cada tipo de inclusión, no existiendo ningún método universal de diseño aplicable a todos los tipos de inclusiones.

La técnica de las inclusiones rígidas se encuentra todavía en desarrollo y expansión, aunque el uso como refuerzo del terreno de pilotes de madera (troncos) recubiertos con una capa de grava date de varios cientos de años.

La comprensión del mecanismo y comportamiento que gobierna el diseño de las inclusiones rígidas comenzó a desarrollarse hace 20 a 30 años y los numerosos éxitos recientes de esta tecnología (particularmente en Europa) han acelerado el camino de la investigación y desarrollo alrededor de las inclusiones rígidas, no únicamente en la vía de desarrollo de nuevos y más potentes equipos sino también en la optimización de la metodología de diseño.

Uno de los mejores modos de describir las inclusiones rígidas es utilizando la definición adoptada por el Programa Francés Nacional (ASIRI, 2012): el concepto de inclusión rígida asume que la estabilidad de la inclusión se obtiene sin confinamiento lateral del terreno circundante (Simon, 2012). En otras palabras, el concepto de inclusiones rígidas abarca todas las inclusiones que presentan una permanente y alta cohesión interna.

Siendo fácil confundir las inclusiones rígidas con la cimentaciones profundas, la presencia de la capa de reparto (LTP) es la llave diferenciadora que lidera y diferencia completamente la distribución de las cargas, la filosofía de funcionamiento y el diseño de las mismas.

Así, aunque parecen equivalentes por el uso de instalaciones y equipos similares, su diseño y ‘funcionamiento interno’ es substancialmente diferente y no deben confundirse una con otra.

En esta segunda parte del artículo, se describen los mecanismos de rotura que se producen en la LTP (capa de transferencia de carga) o capa de colchón de reparto en un sistema de tratamiento mediante inclusiones rígidas y su interacción con los elementos de cimentación como zapatas, losas y soleras.

1. Definición de un tratamiento mediante inclusiones rígidas

Un tratamiento o procedimiento de mejora del terreno mediante inclusiones rígidas combina los siguientes elementos:

Un método de cálculo y dimensionamiento.
Una red de inclusiones con inyección de un mortero/hormigón fluido, a veces, con refuerzos de acero.
Una capa de reparto o de transmisión de cargas (LTP).
Un sistema de control incorporado de la calidad de ejecución de las inclusiones.

La inclusión funciona como un pequeño pilote que cuando se carga moviliza rápidamente el rozamiento lateral tras el cual se moviliza la punta hasta alcanzar la resistencia última fijada a un desplazamiento en cabeza.

Al tratarse de inclusiones con una cohesión permanente, se trata de un método de mejora aplicable en situaciones extremas de resistencia al corte del terreno y de estabilidad lateral. Así son altamente eficientes en terrenos muy deformables debido a que reducen las tensiones que le llegan al terreno y por lo tanto, los tiempos de consolidación.

Esta tecnología utiliza una capa de transferencia de carga (LTP) o colchón de reparto para distribuir las cargas entre las columnas y el terreno ‘in situ’ resolviendo así los siguientes aspectos:

Reducción de las tensiones normales, esfuerzos cortantes y tensiones de compresión y tracción que se concentran en las cabezas de las inclusiones.
Mejora del reparto de las cargas en el caso de solicitaciones no centradas de la zapata en las inclusiones.
Limitación de los esfuerzos parásitos ligados a problemas de excentricidad de las inclusiones.
Homogenización del asiento diferencial generado entre el suelo y las inclusiones, minimizando los esfuerzos de flexión parásitos en soleras y losas.

Como se comprueba, se trata de un elemento fundamental en el diseño de una mejora del terreno mediante inclusiones rígidas.

Recientemente, en Francia se ha desarrollado un programa nacional de investigación llamado ASIRI donde se han analizado los mecanismos de transferencia de carga y su incidencia en los cálculos de elementos de cimentación. En el presente artículo, se recogen los aspectos más relevantes de dicho estudio relacionado con la LTP y nuevos métodos de cálculo de los esfuerzos a flexión generados en los elementos de cimentación.

2. Comportamiento de la LTP o colchón de reparto en un sistema de inclusiones rígidas

En la figura nº1 se muestra el esquema habitual de un tratamiento con inclusiones rígidas con la capa de transferencia de carga o colchón de reparto.

Figura nº 1. Sección tipo mejora del terreno mediante inclusiones rígidas, LTP y carga uniforme.

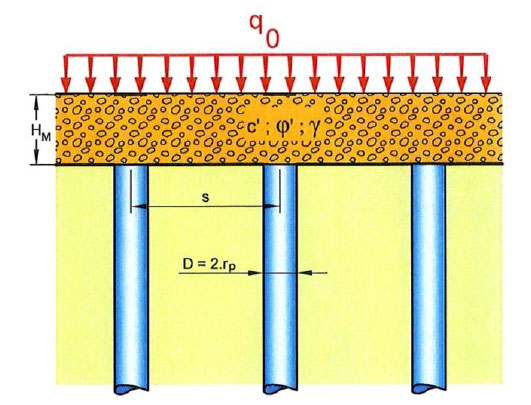
El comportamiento de esta capa depende de diversos factores:

Espaciamiento entre las inclusiones.
Presencia o no de una losa /solera rígida de cimentación.
Grado de compactación (módulo de deformación).
Ángulo de rozamiento interno del material empleado.

Tal y como se indicaba en el artículo anterior, para describir los mecanismos de transferencia conviene distinguir el caso de un terraplén, una losa, una solera o una zapata.

Según los ensayos y comprobaciones llevadas a cabo en el programa ASIRI, la eficacia y comportamiento de esta capa depende de dos mecanismos diferentes:

Mecanismo de rotura de Prandtl, que se desarrolla en casos donde la LTP se sitúa bajo un elemento estructural rígido (soleras, losas o zapatas) o en terraplenes donde se desarrolla el arco completo de transferencia de carga entre inclusiones.
Mecanismo de rotura por punzonamiento del cono invertido, con formación de un cono de cizallamiento centrado bajo la inclusión, y que se desarrolla en caso de terraplenes de poco espesor, donde se cumple la relación: HM< 0,7 (s-D).

2.1. Mecanismo de rotura de Prandtl

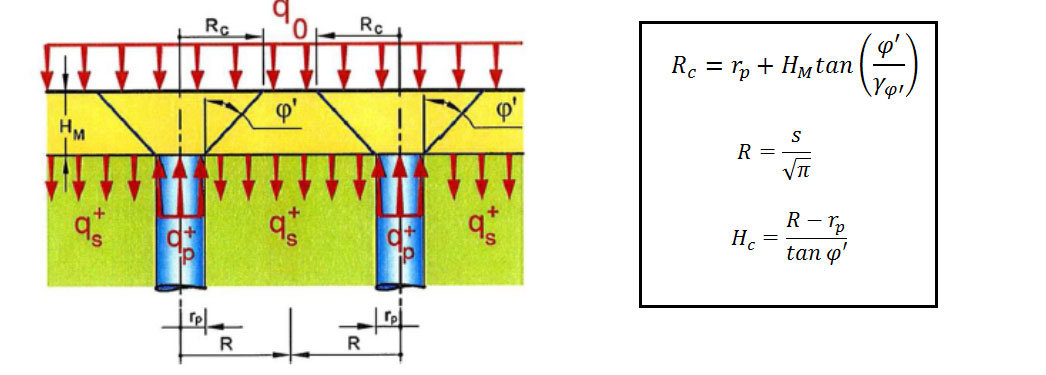
Sin entrar en detalles sobre el criterio de rotura de Prandtl, que se describe ampliamente en la literatura geotécnica, el mecanismo de rotura presenta tres dominios diferentes tal y como se muestra en la figura nº2:

Dominio activo de Rankine (dominio I) justo encima de la cabeza de la inclusión.
Dominio limitado por un arco espiral logarítmico (Dominio II)
Dominio pasivo de Rankine (Dominio III) dentro de la LTP fuera de la influencia de la inclusión.

Figura nº 2. Mecanismo de rotura de Prandtl.

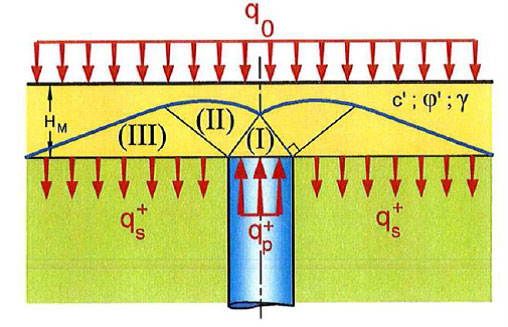
Siendo, (q_p⁺) la carga que recoge la cabeza de la inclusión, (q_s⁺) la carga que se transmite al terreno y (q₀) la carga repartida transmitida por la estructura.

La tensión límite en cabeza (q_p⁺) puede obtenerse a partir de la tensión aplicada al suelo (q_s⁺) y los parámetros intrínsecos de LTP (cohesión, ángulo de rozamiento y densidad) a partir de la siguiente expresión:

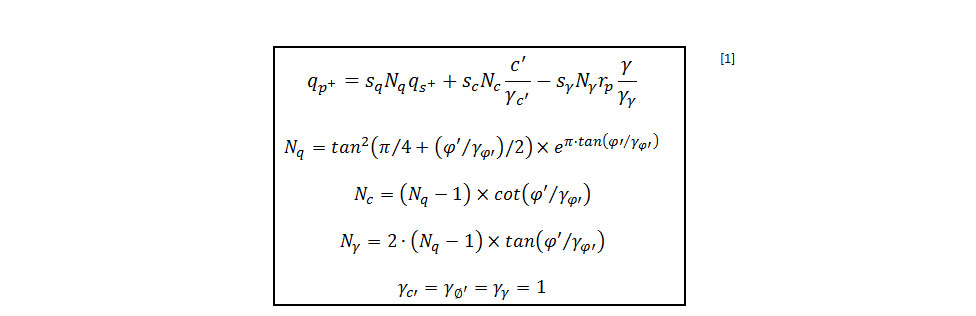
Dicha expresión se reduce en dos de sus términos debido a la escasa incidencia del peso de la LTP y a una cohesión nula de los suelos puramente granulares, reduciéndose la expresión al primer término:

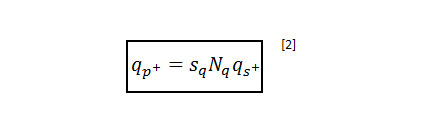
En condiciones de modelos asimétricos o planares de deformación, el valor S_q =1, resultando:

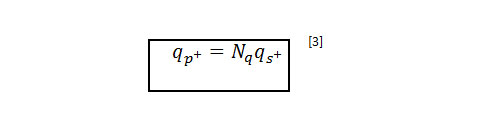
Si consideramos la igualdad de equilibrio de cargas, se obtiene la distribución de cargas del sistema en función del ángulo de rozamiento del material PLT:

2.2 Mecanismo de rotura por punzamiento de cono

El segundo mecanismo, corresponde a un cono vertical desde el borde de la inclusión hasta la parte superior de la LTP (figura nº3), este mecanismo se relaciona con tratamientos que se sitúan bajo rellenos de pequeña altura y donde no hay ningún elemento rígido por encima.

La tensión límite de la cabeza de la inclusión (q_p⁺) se determina a partir de la carga externa aplicada (q_o), el espesor de la capa de reparto (H_m) y los parámetros intrínsecos del material utilizado en el LTP, diferenciándose dos situaciones:

El caso donde el espesor del colchón de reparto (LTP) no llega a desarrollar toda la difusión del cono H_m<H_c:

Figura nº 3. Mecanismo de rotura del cono invertido sin solapes para rellenos de pequeña altura.

La tensión en cabeza (q_p⁺) es el peso del cono más la carga externa aplicada en la parte superior, y se expresa a partir de la siguiente expresión:

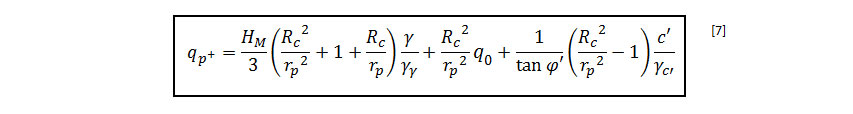
Caso donde el espesor de PLT implique el solape de la difusión del cono, es decir, el espesor del colchón cumple H_m>H_c:

Figura nº 4. Mecanismo de rotura del cono invertido solapado.

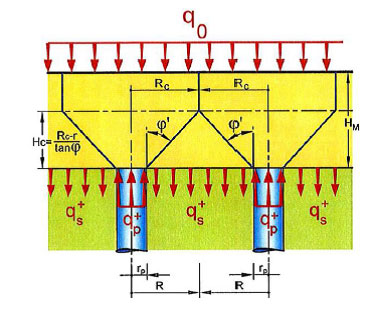
La carga de la cabeza de la inclusión, q_p⁺ es igual al peso del cono más el peso del cilindro de suelo por encima y la carga externa, y se expresa a partir de la siguiente expresión:

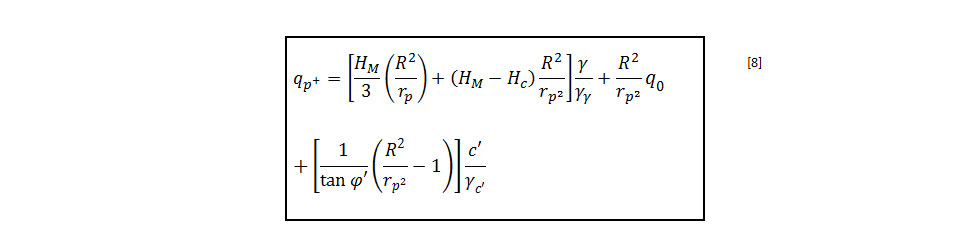
Dominio de esfuerzos según ELU

En las estructuras apoyadas sobre suelos reforzados es común verificar únicamente los estados límites últimos (ELU), relacionados con:

Rotura interna o deformaciones excesivas de los elementos de la estructura en los que la resistencia de los materiales contribuya significativamente a la resistencia global (STR).
Rotura o deformación excesiva del terreno, en los que la resistencia del terreno interviene (GEO).

La máxima carga que puede ser aplicada sobre la cabeza de la inclusión se calcula considerando los ELU los cuales, según el Eurocódigo nº7 (Enfoque 2), combinan los siguientes factores parciales: A1 + M1 + R2

Los factores parciales se aplican a las acciones (A1) o a los efectos de las acciones (acciones permanentes 1,35 y las acciones variables 1,5), los factores de los materiales (M1) a los parámetros del suelo (c, φ, Cu y ϒ) toman el valor de 1 y los factores parciales de resistencia (R2) se definen según el caso:

Cimentaciones superficiales:

Estabilidad: γ_R;v = 1,4
Deslizamiento: γ_R;h = 1,1

Cimentaciones profundas:

Punta: γ_b = 1,1
Fuste: γ_s = 1,1

Junto a estos coeficientes de minoración, las normas NFP francesas también incluyen los factores de incertidumbre del modelo considerando los siguientes valores:

Para proyectos de cimentaciones profundas NF P 94262: γ_R;d= 1,25
Para proyectos de cimentaciones superficiales NF P 94261: γ_R;d = 1,20

La tensión aplicada al suelo (s_vd) en ELU, se limita a la tensión última o de hundimiento sobre el suelo in situ (q_s⁺) según las normas en vigor. Por ejemplo, considerando el método presiométrico y la normativa francesa, se establece según un valor de:

La carga límite aplicada en la cabeza de la inclusión (q_p⁺) está limitada por la capacidad portante de la inclusión (según EC7) y por la tensión admisible en el material empleado, fcd (según EC2), y queda definida por la siguiente expresión:

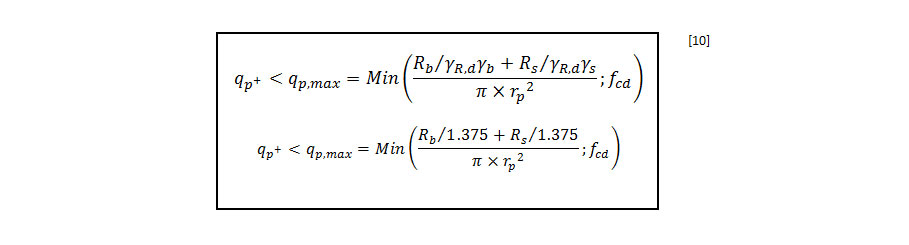
Donde,

R_b es la resistencia última del suelo en punta de la inclusión
R_s es la resultante última de rozamiento lateral bajo el punto neutro.
ϒ_b=ϒ_s=1.1 en ELU
ϒ_{R, d}=1.25
F_cd, la resistencia del hormigón según la siguiente expresión

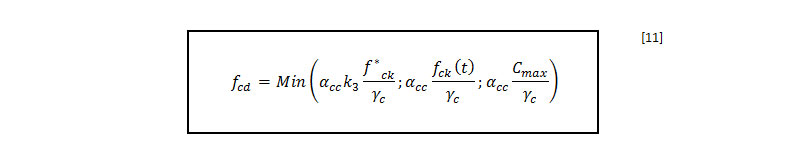
3. Métodos de cálculo de diseño de una solera/losa en un sistema de inclusiones rígidas

En estos casos, el espesor de la capa de reparto o LTP, no permite el desarrollo del arco completo de transferencia, esto provoca una distribución de la tensión no uniforme que genera una tensión adicional que debe tenerse en cuenta en el cálculo estructural.

Para establecer este comportamiento y su interacción en el cálculo estructural, se han llevado a cabo diversos ensayos a escala y modelizaciones con EF proporcionando nuevos métodos para la adaptación del cálculo estructural al sistema de inclusiones rígidas.

a) Método del coeficiente de balasto diferencial

Se trata de un método simplificado para calcular los momentos de flexión en la losa debido a la presencia de las inclusiones rígidas, a partir de establecer los coeficientes de reacción característicos en la zona de influencia de la inclusión y en el terreno entre inclusiones tal y como se muestra en la figura nº10.

Figura nº 10. Modelo del método del coeficiente de balasto ponderado.

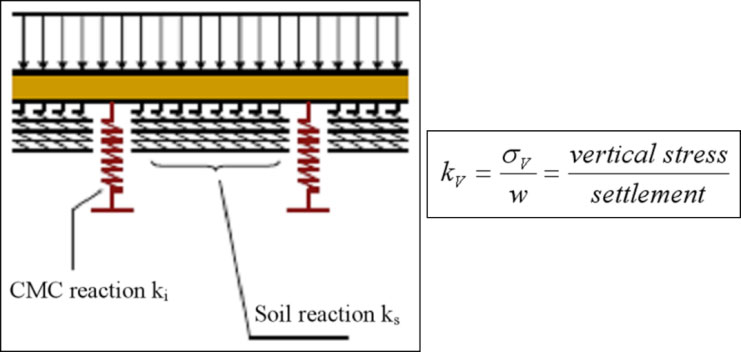
El método se desarrolla en dos etapas, primero se determina la reacción del sistema mediante modelos axisimétricos de elementos finitos (EF) con la parte proporcional de la celda unidad y, en una segunda fase, se ponderan por calibración los coeficientes de balasto a considerar para el cálculo estructural, en función de los resultados de la primera etapa.

Se establece primeramente la distribución de tensiones verticales en la cara inferior de la losa según la malla de separación entre inclusiones y se determina el momento de flexión máximo de referencia (Msup, valor positivo) directamente encima de la inclusión y momento de flexión mínimo (Minf, valor negativo) en la parte central entre inclusiones, tal y como se muestra en la figura nº11.

Figura nº 11. Cálculo axisimétrico con EF para la obtención de la distribución de tensiones y momentos del sistema.

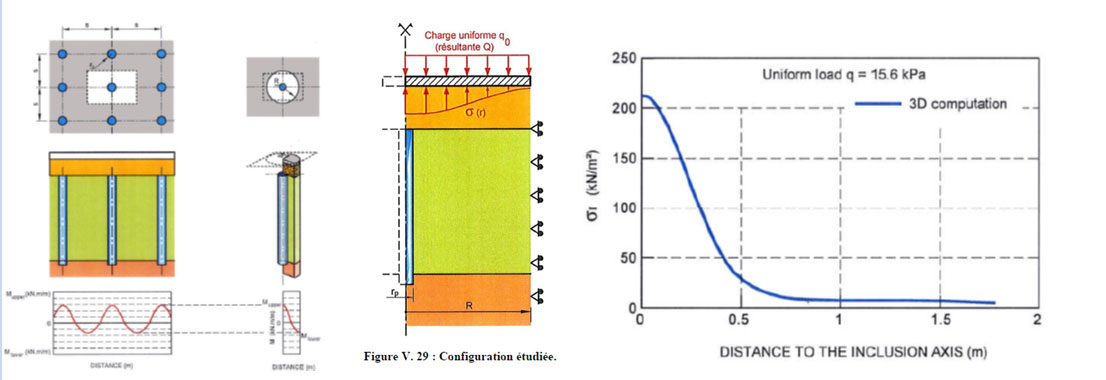
Una vez establecido dichos valores, se procede a la calibración de los coeficientes de balasto. Para ello, en el modelo se establecen dos coeficientes de balasto diferentes: K_i sobre una longitud R_k (influencia de la inclusión) desde el centro de la inclusión, y K_s en el resto de la superficie de cada celda unitaria (K_i> K_s).

Figura nº 12. Estimación de los coeficientes de balasto ponderados.

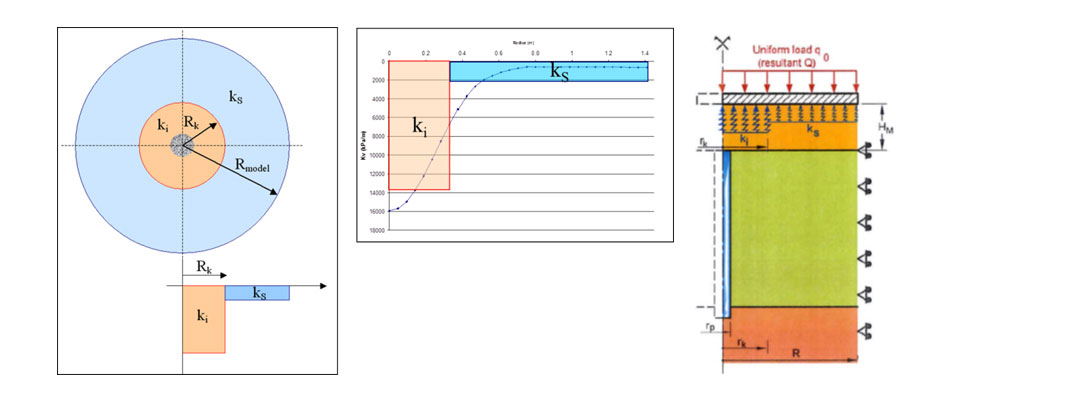
Los momentos en la losa son evaluados utilizando los dos módulos K_i y K_s. La influencia de la inclusión R_k se cambia hasta que haya una estrecha relación entre el valor calculado con los coeficientes de balasto y el cálculo de referencia mediante elementos finitos, para ello se establece la siguiente metodología:

k_s, se calcula considerando el valor mínimo de la tensión aplicada sobre el suelo σ_s en la cara inferior de la losa y el asiento medio de la losa.
Para un valor de R_k, elegido en el intervalo [r_p, r_p +H_m], K_i se calcula con la tensión σi a partir de la ecuación de conservación de la carga total aplicada Q en la malla:

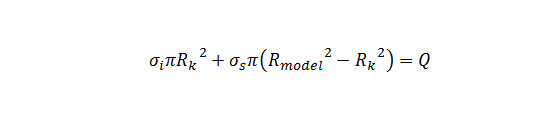
Se calcula la distribución de los momentos a flexión para una carga uniformemente distribuida Q para una placa circular de radio R que apoya sobre los muelles de ki intervalo [0, R_k] y ks en [R_k, R_model].
El valor R_k a obtener es el que mejor se adapte a la curva de momentos establecida en la etapa 1 tanto para el valor Minf como Msup.

En la siguiente figura se muestra un ejemplo de esta metodología realizada mediante FLAC3D, comprobando como el momento máximo tiende a disminuir cuando aumenta R_k. En este caso, para R_k=0,5 se obtienen los valores Minf y Msup acorde con los valores de cálculo con EF.

Figura nº 13. Distribución de coeficientes de reacción para diferentes valores Rk

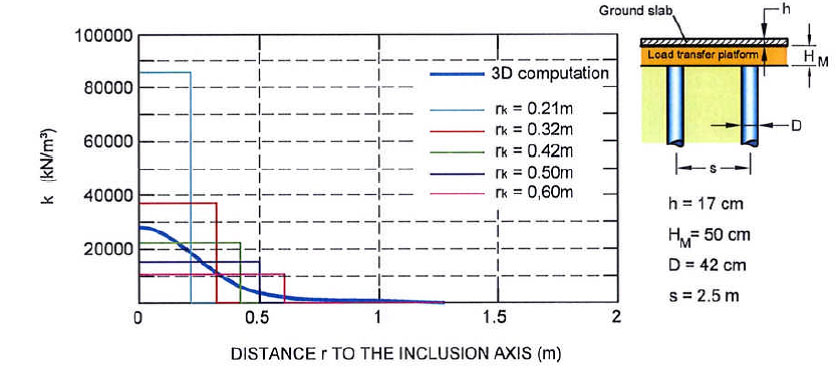
Una vez establecidos los valores correctos de Ki y el Ks, se comprueba el diseño para las diferentes cargas y configuraciones de juntas, comprobando para cada configuración posible los momentos (Msup, Minf) resultantes.

Este método es de aplicación a las zonas centrales cargadas, fuera de las zonas de borde y es necesario examinar las configuraciones de carga más pésimas.

b) Método de los Momentos Adicionales

Este método de optimización del diseño de losas, tiene en cuenta los diferentes tipos de carga y configuraciones (carga uniforme o alterna, estanterías, cargas vivas, …), posiciones relativas de las juntas de construcción y la distribución o malla de inclusiones.

El método consiste en definir términos correctivos ligados a la presencia de las inclusiones rígidas que se añaden a las solicitaciones de la losa (momentos flectores) calculados sobre un suelo homogéneo equivalente.

Se descompone la problemática de diseño en tres términos, denominados:

(ma): resultante del cálculo de una losa sobre un suelo homogéneo equivalente.
(mb): influencia de las inclusiones rígidas sobre una losa continua.
(mc): interacción entre las inclusiones y las juntas

Cada uno de estos términos se evalúa por separado.

Por definición, para cualquier tipo de posibles cargas, se tendrían los siguientes parámetros:

S_oed (NJ): resultante de cálculo de una losa continua que reposa sobre un suelo homogéneo equivalente
S_oed (WJ): resultante de cálculo de una losa con juntas que reposa sobre un suelo homogéneo equivalente
IR (NJ): resultante de cálculo de una losa continua que reposa sobre una red de inclusiones
IR (WT): resultante de cálculo de una losa con juntas que reposa sobre una red de inclusiones

Independientemente del tipo de carga considerada, se puede escribir la siguiente igualdad:

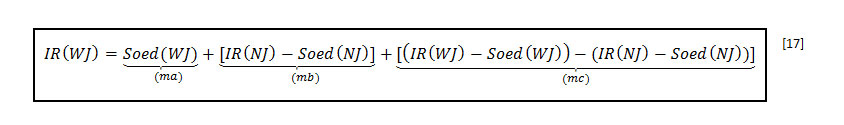
Para establecer los valores de los diferentes términos, se recomienda las siguientes metodologías:

1) El término ‘ma’: cálculo de una losa sobre suelo homogéneo equivalente

El término S_oed (WJ) representa el impacto de la configuración de cargas en una losa con juntas sobre un suelo homogéneo equivalente (reacción uniforme), sin considerar el efecto de los asientos diferenciales que se generan en un sistema de inclusiones rígidas como se ha visto en los apartados anteriores del artículo. Estos valores son proporcionados por el diseñador de la losa para todas las configuraciones y posiciones relativas entre las cargas y las juntas.

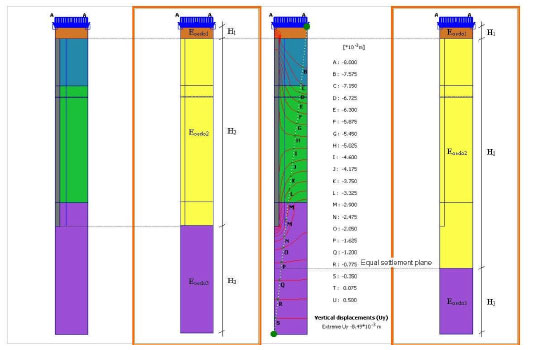
En términos de deformación, un suelo reforzado con inclusiones rígidas puede representarse como un suelo equivalente según la mejora del terreno a través de un módulo de Young equivalente, y un coeficiente de poisson (ver figura nº14). Se puede establecer a partir de modelos de cálculo axisimétricos que permiten obtener el asiento y el módulo de deformación.

Figura nº 14. Modelos equivalentes de suelos reforzados mediante inclusiones rígidas.

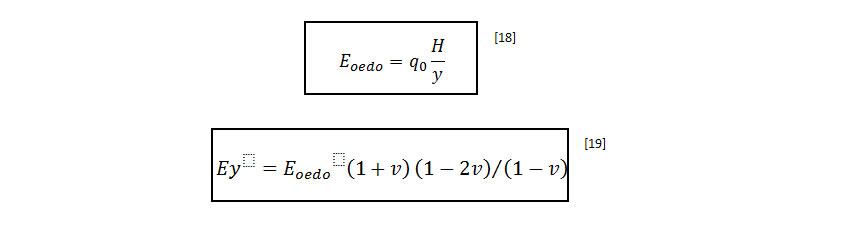
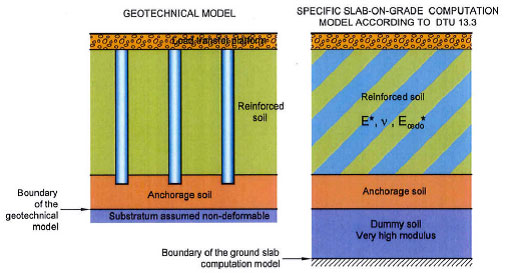
Este módulo se descompone en un mínimo de tres términos relativos a las tres capas que descansan sobre un sustrato supuesto indeformable:

Capa de reparto: altura h1, módulo E1
Suelo reforzado: altura h2, módulo E2
Suelo bajo el suelo reforzado: altura h3, módulo E3

Los valores E1 y E3 son comunes, y el módulo E2 se deduce de la fórmula:

Figura nº 15. Estimación de los módulos equivalentes según método de cálculo axisimétrico.

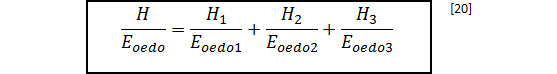
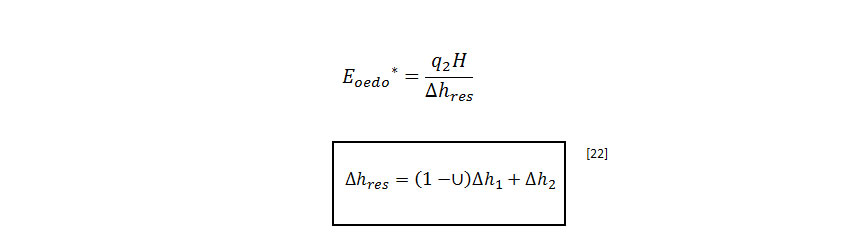
Debe destacarse que, según la norma DTU13.3, los módulos equivalentes para el estudio específico se evalúan a partir de los asientos residuales antes de la construcción (es decir, es necesario tener en cuenta la velocidad de consolidación) y se aplicaran a la carga de explotación (q₂).

2) El término ‘mb’: influencia de las inclusiones en una losa continua

El termino - [IR (NJ) - _soed (NJ)] representa la contribución de las inclusiones rígidas a una losa sin tener en cuenta las juntas.

Para cualquier tipo de carga, el término ‘mb’ se evalúa según modelos axisimétricos sometidos a una carga q_o. Tal y como se reflejaba en la figura nº11, se establece el valor de los momentos Msup y Minf, teniendo en cuenta:

El momento Msup representa el momento radial obtenido en la vertical de la inclusión Mr (r=0)
El momento Minf igual representa el momento radial obtenido en el borde del modelo asimétrico Mr (r=√(A/π)) donde A es la superficie de la malla.

3) El término ‘mc’: interacción entre las inclusiones rígidas y las juntas

El termino [(IR (WJ) - _soed (WJ)) - (IR (NJ) - _soed (NJ))] representa la influencia de la interacción de las inclusiones rígidas y las juntas articuladas. El efecto principal de las juntas es un momento nulo y una redistribución del diagrama de momentos de flexión que se desplaza en las proximidades de las juntas.

El peor de los casos es que una junta y una inclusión rígida estén alineadas. En este caso, el momento encima de la inclusión M_supes 0, y un desplazamiento neto de -M_sup. De manera similar, si la articulación está situada exactamente en la mitad entre dos inclusiones, entonces los momentos cambian, M_infes 0 (y un desplazamiento de M-_inf).

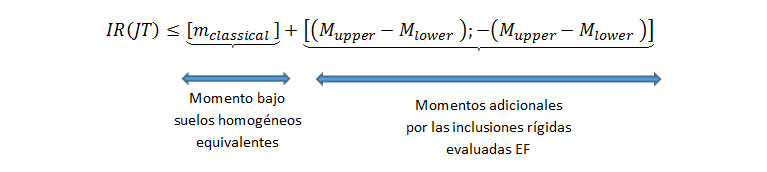
Por lo tanto, podemos definir una envolvente de momentos [mc] = [M-_inf; - M _sup]. Esto permite la asignación de un rango seguro y una gama de valores que pueden ser afinados teniendo en cuenta la peor configuración de las inclusiones rígidas con respecto a las juntas.

En la figura nº16 se muestra la posición de las juntas (líneas verdes) en las zonas donde se tiene un M=0 según la disposición de las inclusiones.

Figura nº 16. Ejemplo de valores parámetro mc.

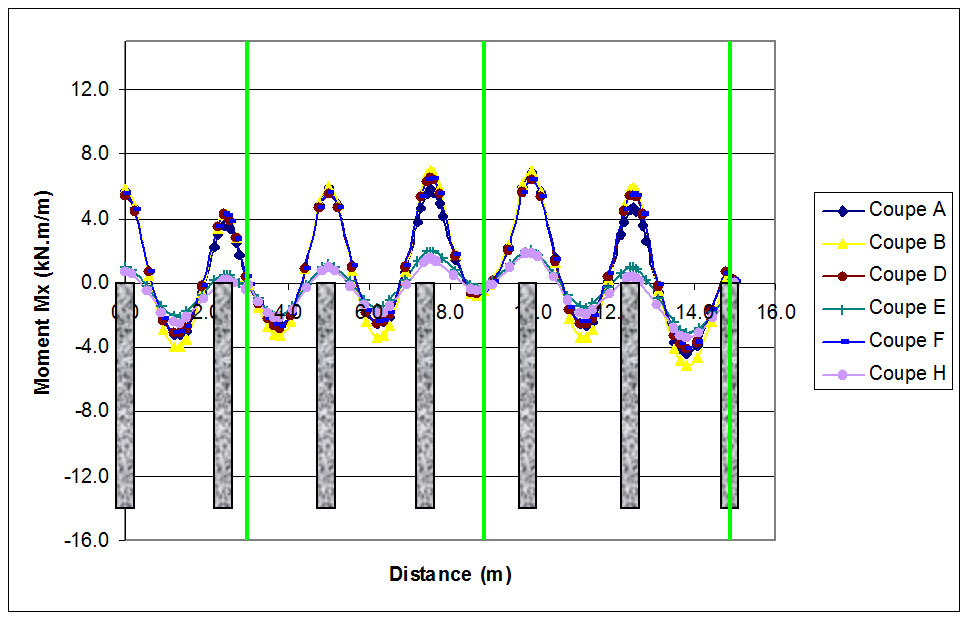
Por lo tanto, es posible determinar una envolvente de momentos que delimita la distribución del momento real, a través de cálculos simples se introduce en el cálculo estructural los efectos de la influencia de las inclusiones en los momentos parásitos que se generan como consecuencia de la reacción no uniforme de los asientos.

Conclusiones

La mejor manera de determinar las deformaciones de un sistema de mejora del suelo con inclusiones rígidas es a través del uso de elementos finitos o de diferencias finitas.

Si bien los cálculos axisimétricos se usan principalmente en configuraciones simétricas (por ejemplo, un patrón de inclusiones en la parte central de una losa), muchas situaciones requieren de modelizaciones más avanzadas, que permiten el estudio de las condiciones no uniformes en el borde del modelo, y situaciones de disimetría de cargas.

Se ha comprobado que en la cabeza de las inclusiones el fenómeno predominante es la transferencia de carga a través del cizallamiento, por ello es fundamental establecer los parámetros y leyes de comportamiento de los materiales que constituyen el colchón de reparto o LTP.

Por último, se han descrito dos métodos de diseño geotécnico que permiten evaluar el comportamiento de la interacción estructura-tratamiento por inclusiones rígidas a través de una ponderación en el coeficiente de reacción o de balasto y envolvente de momentos adicionales.

En los casos en los que la constitución del colchón de reparto conlleve una excavación o retirada de elementos existentes estructurales, es necesario facilitar el fenómeno de transmisión de cargas con elementos flexibles en la cabeza de inclusiones.

Así, a menudo, se ejecutan columnas hibridas o ‘Bi-modulo’ las cuales presentan comportamiento y características de inclusiones rígidas con una cabeza granular flexible que permite la transferencia de cargas acorde a los descrito en el presente artículo.

En próximos artículos describiremos la ejecución y dimensionamiento de las mismas.

Nomenclatura

A_c:Superficie o área de la inclusión	F_ck(f): Valor de cálculo de la resistencia a la compresión del hormigón, lechada o mortero a los t días.	K_3:Coeficiente para determinar el valor de la resistencia a compresión del hormigón según el tipo de control	R: Radio de la malla equivalente	α: Tasa de sustitución.	g_R;v:Factor parcial por la capacidad de carga (resistencia).
A_s:Superficie o área del suelo flojo	F_ck^:*Valor de cálculo de la resistencia a la compresión del hormigón, lechada o mortero usada en una inclusión.	N_c, N_q, N_g:Factores de capacidad de carga.	R_b:Resistencia en punta de la inclusión	α_cc:Coeficiente para el cálculo de la resistencia característica del hormigón.	g_b:Factor parcial por la resistencia en punta de la inclusión.
C_max:Valor máximo de resistencia a compresión del hormigón teniendo en cuenta la construcción y el método de ejecución	f_c28:Valor característico de la resistencia a la compresión a 28 días.	p_l^:*Presión limite neta o corregida.	R_C:Radio máximo de la difusión del cono.	Ф’: Ángulo de rozamiento interno efectivo.	g_c’:Factor parcial para la cohesión efectiva
c’: Consistencia (en términos de tensión efectiva)	H: Altura del terreno compresible.	p_lim:Valor final de la presión lateral del suelo contra una inclusión.	R_k:Valor característico de la resistencia.	g: Unidad de peso del suelo.	g_S:Factor parcial de resistencia por fuste de la inclusión.
D: Diámetro de inclusión	H_M ou h_m:Altura o espesor de la plataforma.	Q: Carga vertical neta del sistema de carga.	R_s:Resistencia final movilizada por fuste de la inclusión	g^’:Unidad de peso sumergido del suelo.	g_Ф’:Factor parcial para el ángulo de fricción interno (tan_Ф’).
E: Eficacia de la carga	h: Espesor de la losa/solera.	q_0:Tensión aplicada	r_k:Radio que define la distribución de los coeficientes de reacción subrasante k_iy k_s	g_C : Coeficiente parcial relativo del hormigón.	g_g:Factor parcial para la unidad de peso.
Ey: Módulo de Young, Módulo de Elasticidad	k_sou k_s:Coeficiente de Reacción subrasante de suelos	q_p^+:Tensión aplicada a la cabeza de la inclusión.	s_s:Esfuerzo vertical uniforme bajo una losa en el intervalo r_k≤r≤R	g_G:Factor parcial para una acción permanente	v: Coeficiente de Poisson.
E_oed:Módulo Edométrico	K_p:Factor de carga presiométrica.	gs: Unidad de peso del suelo.	r_p:Radio de inclusión.	g_Q:Factor parcial de acciones variables	s: Tensión total.
f_cd:Valor de cálculo de la resistencia de compresión del hormigón, lechada o mortero usado en una inclusión.	k_i:Coeficiente de Reacción subrasante en la parte inferior de la losa adyacente al eje de las inclusiones rígidas (rk).	q_p,d^+:Valor límite de cálculo de la tensión aplicada a la cabeza de la inclusión.	S_c,s_g, s_q:Coeficientes de forma para el cálculo de capacidad portante.	g_R;h:Factor parcial frente al deslizamiento	s_i:Tensión vertical asumida uniformemente sobre el disco r ≤ r_ken la parte inferior de la placa
fck: Valor de cálculo de la resistencia a la compresión del hormigón, lechada o mortero a los 28 días.	k_s:Coeficiente de Reacción subrasante del suelo blando en la parte inferior de apoyo de la losa en la zona fuera de la inclusión (r>r_k).	q_s^+:Tensión aplicada a los suelos blandos.	U: Grado de consolidación.	g_R;d:Factor parcial por el nivel de incertidumbre	s_v,d:Valor de cálculo final de la tensión vertical en la superficie del terreno.

Referencias bibliográficas

ASIRI, ”Recommendations for the design, construction and control of rigid inclusions ground improvements”. Presses des Ponts et Chaussées. IBN 978-2-85978-462-1.
BUSCHEMEIER B, MASSE F “Discussion of differences in design methodology between granular and grouted inclusions”. XXVI Reunión Nacional de Mecánica de suelos e Ingeniería Geotécnica, Cancún, México Nov 2012.
VARAKSIN S, HAMIDI B, RACINAIS J “The thin line between Deep foundations and soil improvement” Proceeding of the international Conference on Integrate Use and Protection of underground spaces, Kungur Ice Cave, Perm Region, Russian, May 2014.