Automatización
Efectos dinámicos de los elementos activos de los manipuladores en la resolución del problema dinámico inverso
S. Provenzano1, V. Mata2 and M. Vergar1, 1Universidad de Los Andes ,
Fac. de Ingeniería, Mérida 2 Universidad Politécnica de Valencia,
D. de Ingeniería Mecánica y Materiales, Valencia 46022, España15/06/2004
Fac. de Ingeniería, Mérida 2 Universidad Politécnica de Valencia,
D. de Ingeniería Mecánica y Materiales, Valencia 46022, España15/06/2004
En este trabajo se desarrolla una formulación O(n) que permite resolver el problema dinámico inverso de robots de tipo cadena abierta, tomando en cuenta los efectos inerciales debidos al movimiento de los rotores de los actuadores. La formulación se obtiene de manera natural a partir de las ecuaciones de la dinámica de Gibbs-Appell. Para validar los resultados, se emplea un ejemplo de un manipulador tres grados de libertad, el cual es resuelto por medio de la formulación propuesta en este trabajo y comparada con otra conocida formulación.
La mayoría de los nudos en los robots industriales son accionados por motores con elevadas relaciones de transmisión. Usualmente no es tomado en cuenta el efecto del movimiento de los rotores en las ecuaciones de la dinámica de los manipuladores, pero es evidente que si se emplean altas relaciones de transmisión y el sistema se mueve a elevadas velocidades, este efecto podría ser relevante. La incorporación, en la ecuación que modela la dinámica de robots manipuladores, de los efectos de los rotores de los actuadores, genera cambios en las formulaciones empleadas para resolver tanto el problema dinámico inverso (PDI) como el directo. Las formulaciones que resuelven estos problemas de manera eficiente han sido desarrolladas por diferentes autores empleando diversos principios de la dinámica, encontrándose que las formulaciones que dan como resultado algoritmos eficientes, son los de tipo recursivo [1, 2]. Usualmente, la incorporación de los efectos de los elementos activos en las ecuaciones de la dinámica se efectúa de manera simplificada [3]. Sin embargo, se ha demostrado que el método simplificado puede ocasionar errores significativos en nudos de manipuladores que cuentan con relaciones de transmisión elevadas [4]. En el desarrollo de las formulaciones que toman en cuenta el movimiento de los elementos activos, los autores han empleado fundamentalmente las ecuaciones de Lagrange y las de Newton-Euler [4,5]. Pocos autores han publicado trabajos en los cuales se emplean otros principios de la dinámica para tomar en cuenta el efecto de los elementos activos en las ecuaciones que modelan el movimiento de un manipulador. Por ejemplo, en [6] los autores resuelven el PDI de manipuladores, tomando en cuenta el efecto de los elementos activos, a través de una formulación de orden O(n2) basada en las ecuaciones de Gibbs-Appell. La mayoría de los algoritmos eficientes desarrollados para resolver el PDI, sin importar en cual principio de la dinámica se basen, son recursivos y suelen ser aplicables a una gran variedad de robots industriales. Esto último es posible gracias a que una gran parte de los manipuladores poseen estructuras del tipo cadena abierta y los nudos que unen sus barras son pares de revolución o prismáticos, reduciendo de esta manera la cantidad de factores a tomar en cuenta. Estas ventajas, en cuanto a la similitud de configuraciones cinemáticas, desaparece cuando se toman en cuenta los elementos activos, ya que los motores que accionan los nudos en los diferentes robots manipuladores se instalan en una gran variedad de configuraciones, obligando a desarrollar formulaciones específicas para cada manipulador. Es por lo tanto un paso ineludible, antes de desarrollar una formulación para resolver cualquiera de los problemas dinámicos, definir una configuración cinemática genérica para desarrollar una formulación que pueda ser posteriormente modificada con poco esfuerzo para adaptarla a las diferentes configuraciones de manipuladores existentes. En este trabajo se emplean las ecuaciones de Gibbs-Appell para desarrollar un algoritmo recursivo de orden O(n) para resolver el PDI de robots manipuladores, tomando en cuenta el efecto causado por el movimiento de los rotores de los actuadores.
Notación
Típicamente, los manipuladores son cadenas abiertas formadas por n+1 cuerpos rígidos unidos entre sí por medio de n nudos de revolución o prismáticos. Los actuadores que mueven los diferentes nudos se instalan sobre cuerpos que componen la cadena abierta. En el desarrollo de la formulación que se propone en este trabajo se emplea una configuración simple en la cual el motor que acciona cada barra se encuentra instalado en la barra precedente, accionando un nudo de revolución, tal y como se muestra en la Figura 1. Para la colocación e identificación de los sistemas coordenados ligados a los cuerpos y a los rotores se emplea una notación basada en la de Denavit-Hartenberg (D-H) modificada [7]. En la notación empleada, cada i-ésimo motor está rígidamente unido a la barra i-1. En cada motor se considera un sistema de referencia ligado a la parte fija del propio motor,
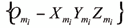
El sistema coordenado ligado a la barra i-1 está relacionado al sistema ligado al motor i mediante una matriz de rotación i-1R mi, mientras que el rotor i y la barra i se relacionan mediante la relación de transmisión
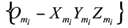
La definición del sistema de referencia se hace de
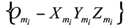
acuerdo con la notación de D-H modificada [8] con respecto al sistema de referencia ligado a la propia barra i-1, esto es, el
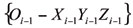
(Figura 2).
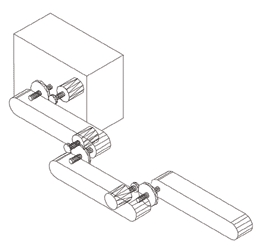
Figura 1.- Disposición de motores
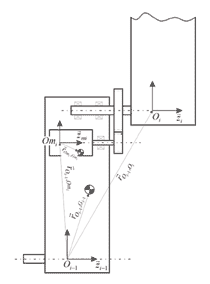
Figura 2.- Notación empleada
La relación entre ambos sistemas de referencia se establecerá mediante los 4 parámetros siguientes:
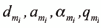
Obsérvese que los primeros tres parámetros son constantes, dependientes de la geometría de la barra i y de la localización del motor. La siguiente matriz de transformación homogénea relaciona ambos sistemas coordenados:
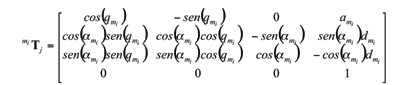
A continuación se definen las ecuaciones cinemáticas recursivas que permiten calcular las velocidades y aceleraciones de los rotores, en función de las velocidades y aceleraciones de las barras:
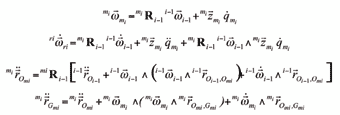
donde la matriz de rotación miR i-l se extrae de la matriz de transformación homogénea (1), al igual que el vector
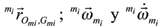
y son los vectores velocidad y aceleración angular del rotor i (el cual acciona a la barra i),
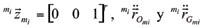
y son los vectores aceleración del origen y del centro de masas del rotor i, todos ellos expresados en base al sistema coordenado ligado al rotor i; igualmente
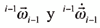
y son los vectores velocidad y aceleración angular de la barra i-1,
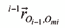
es el vector posición que relaciona el origen del sistema coordenado ligado a la barra i-1 con el origen del sistema coordenado ligado al rotor i,
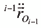
es la aceleración del origen del sistema coordenado ligado a la barra i-1, estos últimos expresados en el sistema coordenado ligado a la barra i-1. La relación de transmisión _i relaciona la posición, velocidad y aceleración del nudo i, con la posición, velocidad y aceleración del rotor i:
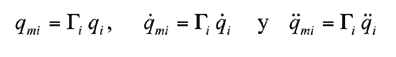
Resolución del problema dinámico inverso
En esta sección se emplean las ecuaciones de Gibbs-Appell y la notación descrita en la sección anterior para desarrollar una formulación recursiva de orden O(n) que permite resolver el problema dinámico inverso de robots manipuladores tomando en cuenta la inercia de los rotores de los actuadores. El empleo de las ecuaciones de Gibbs-Appell proporciona una manera muy simple de incorporar al modelo del sistema el efecto dinámico causado por la rotación de los rotores. Las ecuaciones de Gibbs-Appell parten de la definición de la función de Gibbs, también conocida como energía de las aceleraciones, la cual escrita en su forma original para un sólido arbitrario compuesto por n partículas elementales [9]:
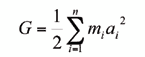
El efecto inercial de la rotación de los rotores en el movimiento de un manipulador puede tomarse en cuenta sumando la función de Gibbs debida al movimiento de las barras y la función de Gibbs debida a la de rotación de los rotores:
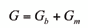
Estas dos funciones pueden ser calculadas de manera separada, para ello es necesario conocer la cinemática de las barras. Se hallan entonces las fuerzas generalizadas debidas al movimiento de las barras y a éstas se suman las fuerzas generalizadas debidas al movimiento de los rotores [9]:
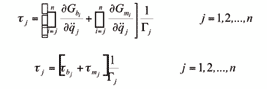
La participación del movimiento de las barras en las fuerzas generalizadas, empleando las ecuaciones de Gibbs-Appell, puede ser calculada eficientemente por medio de procedimientos recursivos que han sido obtenidos anteriormente [10]. Dichos procedimientos recursivos se basan en la ecuación:
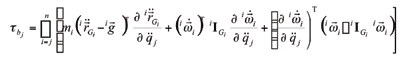
donde mi es la masa de la barra i, iI Gi es el tensor de inercia con respecto al centro de masa de la barra i
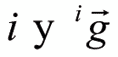
y es el vector aceleración de gravedad, los dos últimos expresados en el sistema de coordenadas ligado a la barra i. Por otro lado, la participación de la inercia de los rotores en las fuerzas generalizadas puede ser calculada por medio de la siguiente expresión:
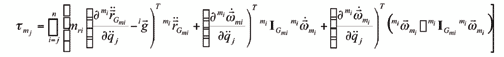
donde mri es la masa del rotor i, mi IGmi es el tensor de inercia con respecto al centro de masa del rotor i expresado en el sistema de coordenadas ligado al rotor i. La expresión (12) permite hallar la contribución de la inercia de los rotores a las fuerzas generalizadas por medio de una formulación de orden O(n2). Como se observa, es necesario hallar las derivadas parciales de las aceleraciones angulares y de los centros de masas de los rotores con respecto a las aceleraciones de los nudos. Estas expresiones pueden ser halladas de manera algebraica para sistemas compuestos por pares de revolución y/o prismáticos, derivando las expresiones recursivas con las que se calculan las aceleraciones angulares y las aceleraciones de los centros de masa. A continuación se muestran las expresiones algebraicas que permiten calcular las derivadas parciales indicadas en la expresión (12), las cuales corresponden a nudos de revolución:
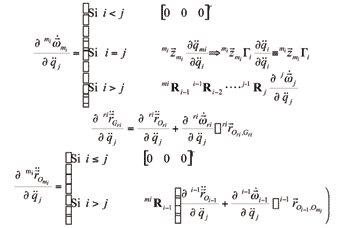
En virtud de las expresiones (13), (14) y (15), la ecuación (12) puede calcularse por medio de un algoritmo sencillo de orden O(n).
La mayoría de los nudos en los robots industriales son accionados por motores con elevadas relaciones de transmisión
Ejemplo
En esta sección se aplica el algoritmo propuesto en la sección anterior para resolver el PDI del manipulador de tres grados de libertad mostrado en la Figura 1. Para ello, el algoritmo ha sido ejecutado en Matlab[11], al igual que el algoritmo propuesto por Murphy[4]. El problema a resolver consiste en hallar los pares que deben suministrar los motores para que el manipulador se mueva, bajo el efecto de la aceleración de gravedad, partiendo de las siguientes posiciones de nudo: q1=0, q2=0, q3=0; con las siguientes velocidades iniciales de nudo
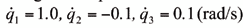
y las siguientes aceleraciones de nudo constantes
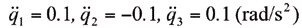
Los nudos del manipulador se mueven durante 0.2 s siguiendo un movimiento uniforme acelerado, esto es:
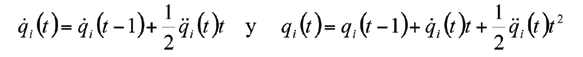
el cómputo del PDI se realiza a intervalos de 0.01 s. Con la finalidad de validar los resultados obtenidos del algoritmo propuesto, éstos se comparan con los resultados obtenidos empleando el algoritmo propuesto por Murphy. Los parámetros D-H y las características del manipulador se muestran en las tablas 1 y 2, es de hacer notar que los orígenes de los sistemas coordenados ligados a los motores se encuentran ubicados en el centro de masas de los mismos. Los resultados obtenidos de ambos algoritmos no presentan diferencias relevantes, tal y como se puede observar en la Tabla 3. En ésta se muestran los valores máximos de las diferencias relativas entre los resultados arrojados por cada uno de los algoritmos, donde se evidencia que las diferencias entre los resultados producidos por ambos algoritmos son prácticamente insignificantes.

Tabla 1 Datos de los barras del robot

Tabla 2 Datos de los motores del robot
Conclusiones
En este trabajo se ha desarrollado una formulación O(n) que permite resolver el PDI de robots manipuladores, tomando en cuenta los efectos inerciales debidos a la rotación de los rotores de los actuadores. La formulación ha sido desarrollada de manera simple empleando las ecuaciones de Gibbs-Appell. Para validar la formulación se resuelve el PDI de un robot genérico de tres grados de libertad empleando la formulación propuesta y la formulación propuesta por Murphy, demostrándose que el algoritmo propuesto en este trabajo proporciona excelentes resultados.

Tabla 3 Diferencias en los pares
En este trabajo se ha desarrollado una formulación O(n) que permite resolver el PDI de robots manipuladores, tomando en cuenta los efectos inerciales debidos a la rotación de los rotores de los actuadores
Referencias
- J. Angeles. Fundamentals of Robotic Mechanical Systems, Nueva York: Springer Verlag, 1997.
- R. Featherstone and D. E. Orin, "Robot Dynamics: Equations and Algorithms", Proc. Of the 2000 IEEE Int. Conf. On Robotics & Automation, San Francisco, Apr. 2000pp. 826-834.
- M. W. Spong, "Modelling and control of elastic joint robots", Journal of Dynamic Systems, Measurement and Control, Vol. 109, Dec, 1987, pp. 310-319.
- Murphy, S. H., Modelling and simulation of multiple cooperating manipulators on a mobile platform 1990. Tesis doctoral,Rensselaer Polythecnic Institute.
- L. Sciavicco, B. Siciliano, and L. Villiani, "Lagrange and Newton-Euler dynamic modelling of gear driven rigid robot manipulator with inclusion of motor inertia effects", Advanced Robotics, Vol. 10, 1996, pp. 317-334.
- K. Desoyer, P. Lugner, and H. Springer, "Dynamic effects of active elements in manip and their influence upon the controlling drives", IUTAM/IFFToMM Symp, Udine, 1985, pp. 44-51.
- J. Angeles and O. Ma, "Dynamic Simulation of n-Axis Serial Robotic Manipulators Using a Natural Orthogonal Complement", Int. Journal of Robotic Research, Vol. 7, 1988, pp. 32-47.
- J. Angeles, O. Ma, and A. Rojas, "An algorithm for the inverse dynamics of n-axis general manipulators using Kane's equations", Computers Math. Applic., Vol. 17, 1989, pp. 1545-1561.
- L. Pars. A Treatise on Analytical Dynamics, Connecticut: Ox Bow Press, 1972.
- V. Mata, S. Provenzano, J. L. Cuadrado, and F. Valero, "Inverse dynamic problem in robots using Gibbs-Appell equations", Robotica, Vol. 20, 2002, pp. 59-67.
- The Mathwork Inc., MATLAB R12, en http:\www.mathwork.com