Diseño optimizado de piezas de plásticos
1. Introducción
Cuando se plantea la creación de una pieza, el diseñador debe tener especial cuidado en considerar todas las variables cuya influencia puede ser importante en el desarrollo del proyecto. Estas variables son las involucradas en cada uno de los pasos intermedios existentes entre la aparición del concepto inicial del producto y su fabricación. Por lo tanto, el diseñador debe conocer las particularidades de los materiales con los que trabaja, las condiciones operativas de la pieza, las que impone el método de fabricación y la viabilidad económica del proyecto.
La tarea es a menudo compleja y, en muchas ocasiones, los resultados no siempre concuerdan con la idea original o bien esta idea debe ser replanteada ante la imposibilidad de su puesta en práctica.
La forma tradicional de abordar el diseño de una pieza de plástico inyectada parte de una propuesta básica junto con la elección de un determinado material. A continuación, y siguiendo etapas secuenciales, el modelo se depura a fin de conseguir las características de rigidez y consistencia deseadas.
Sin embargo, cuestiones como la influencia de las condiciones de transformación sobre el comportamiento posterior de la pieza o la consideración de las acciones externas que la misma pudiera soportar a lo largo de su vida útil -extremadamente difíciles de evaluar a priori- obligan a trabajar con un elevado nivel de incertidumbre y a emplear factores de seguridad elevados. Esto lleva a fabricar artículos sobredimensionados o con grandes espesores de pared.
Por otra parte, el máximo espesor de los artículos inyectados está limitado por el proceso de inyección y las contracciones que sufre el material en el interior del molde. Así pues, para obtener idénticas prestaciones mecánicas con espesores reducidos, la pieza debe nerviarse de forma abundante con los procesos tradicionales.
La propia naturaleza iterativa del diseño en ingeniería ha hecho que la consecución de un diseño óptimo requiera de la realización de numerosas pruebas, pues cada cambio efectuado en una etapa puede eventualmente afectar al resto. Así mismo, la presencia de un equipo experto ha sido condición imprescindible para acometer con garantías de éxito la construcción del molde de inyección, asegurar la fiabilidad de la pieza y pasar a su fabricación en serie.
En el mercado actual, la calidad o la ausencia total de defectos en un proyecto es un requisito insoslayable para cualquier fabricante. Conseguirlo implica destinar mayores recursos al mismo; esto es, el empleo de más dinero, personal y tiempo. Así ocurre que los costes de desarrollo aumentan considerablemente y por tanto se pierde competitividad.
La solución a este problema radica en una utilización efectiva de los recursos, y es aquí donde las nuevas tecnologías CAD/CAE para el diseño de piezas [1] encuentran su mayor aplicación.
Hasta hace relativamente pocos años, estos programas veían limitada su aplicación por la necesidad de invertir grandes sumas en la adquisición de complejos equipos informáticos. En la actualidad y gracias a los continuos avances de la microinformática, la aparición de ordenadores más rápidos y potentes a bajo precio ha hecho posible su generalización. Sin embargo, mientras las técnicas y programas de diseño asistido por ordenador (CAD) son de uso común en casi todas las empresas, las técnicas de ingeniería asistida por ordenador (CAE) no han alcanzado, todavía, la difusión de las anteriores. Es importante destacar que la verdadera ventaja competitiva se obtiene de la utilización conjunta de ambas técnicas y de su aplicación paralela al diseño [2].
La mayoría de los paquetes de software se basan en técnicas de discretización por elementos finitos y son de aplicación general a todo tipo de materiales, aunque en el caso de los plásticos existen programas específicos que simulan las condiciones del proceso de inyección y que disponen de una muy amplia librería de familias, variedades y grados de plásticos así como de todas sus características [3].
Este artículo se centra en el proceso de cálculo mecánico de piezas, para lo cual se expone, a modo de ejemplo, el cálculo de la carcasa de una bomba periférica para agua en plástico.
2. El método de elementos finitos
Los principios matemáticos en que se basa el método de los elementos finitos están bien descritos en la literatura [4-6] y son ampliamente utilizados en ingeniería [7-8]. En realidad, su filosofía es muy sencilla. La idea principal del método consiste en sustituir la pieza como entidad continua por una serie de partes o porciones pequeñas de geometría sencilla, sobre las que se aplican las ecuaciones de la mecánica. De este modo se reduce un problema con infinitos grados de libertad a uno que tiene un número de variables finito.
Cada porción o elemento en que se subdivide la pieza (ver la figura 1) posee sus mismas características, como material, propiedades o espesor. Los puntos de interconexión entre elementos se conocen como puntos nodales o nodos.
Figura 1 Nodos y elementos
La evolución de cada elemento queda determinada por un numero de parámetros o grados de libertad, que se asocian a los nodos y por una función de interpolación. Así, el comportamiento de un elemento se extrae o interpola a partir de lo que sucede en cada uno de sus nodos. La respuesta de la pieza completa quedará determinada por asociación de sus elementos componentes.
Podemos concluir, por lo tanto, que el análisis por elementos finitos es un método aproximado de cálculo que, aplicado a un modelo idealizado, permite averiguar su comportamiento. Dicho comportamiento se obtiene por la resolución de un sistema de ecuaciones matemáticas con número finito de variables que se utiliza para describir el modelo.
3. Etapas de análisis
Los programas de cálculo por elementos finitos son herramientas de programación muy potentes y versátiles. De ahí que para su mejor comprensión se suelen estructurar en una serie de etapas básicas que, a su vez, se desglosan en más pasos simples. En la figura 2 se distiguen las diversas partes que configuran un proceso de diseño mediante elementos finitos: preprocesa, análisis y postprocesado.
3.1. Preprocesado
El preprocesado incluye todas aquellas acciones que son necesarias para la formulación unívoca del problema. Así, el programa genera una serie de archivos de datos en los que se guardan las características de la pieza, datos que pueden ser actualizados o cambiados con facilidad en cada iteración.
3.1.1. Geometría
En un proceso lógico, la primera necesidad es generar la geometría del problema. Esta concepción preliminar del proyecto debe crearse considerando las limitaciones, condicionantes y requerimientos funcionales del artículo (figura 3). No tiene ningún sentido tratar de optimizar una pieza cuya forma no concuerda con las especificaciones formuladas, pues obtendremos un diseño excelente para una solución errónea.
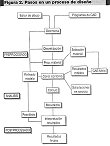Figura 2 Pasos en un proceso de diseño
La geometría puede importarse desde programas específicos de CAD a través de módulos que interpretan automáticamente las entidades, puntos, curvas o superficies del modelo o bien puede generarse a través de un editor de dibujo del propio programa.
Es conveniente aprovechar las simetrías y evitar, por ejemplo, detalles en zonas a priori no importantes o no críticas. En definitiva, debe eliminarse todo aquello que en esta primera fase pueda suponer un gasto de tiempo y esfuerzos innecesario. Del cálculo con un modelo sencillo podremos ver cuales serán los lugares más comprometidos y que requerirán de mayor atención y detalle. Incluso puede ocurrir que este primer cálculo ocasionara cambios importantes en la forma de la pieza, con lo que nada se hubiera ganado con una definición muy exhaustiva, antes al contrario, hubiera supuesto una pérdida importante de dinero. Así, la primera regla del modelado consiste en comenzar con una estructura sencilla para con posterioridad optimizarla.
Figura 3 Requerimientos funcionales de una pieza
Las figuras 4 y 5 muestran la geometría de la carcasa y tapa de la bomba. Ambas partes se han analizado conjuntamente para tener en cuenta su influencia mutua.
Figura 4 Geometrína del cuerpo de bomba
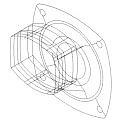Figura 5 Geometría de la tapa de bomba
El estudio que se lleva a cabo tiene como objetivo comprobar la viabilidad de la sustitución del material con el que se fabrica la carcasa (poliarialmida IXEF 1022 de Solvay) por otro material plástico de prestaciones semejantes y menor precio. En este sentido se ha determinado que el polipropileno cargado con un 30% de fibra de vidrio puede resultar válido para este propósito.
Una de las especificaciones de funcionamiento de la carcasa consiste en mantener la estanqueidad entre sus dos partes constituyentes. De esta constatación, la máxima flecha admisible es de 0,5 mm. Esta flecha es la que absorbe la junta estanca que se monta entre cuerpo y tapa de la bomba. Otra de las condiciones del fabricante es mantener invariable la geometría, puesto que de este modo puede aprovecharse el molde de inyección con el que se fabrican las bombas actuales.
Figura 6 Modelo de discretización
Figura 7 Efecto de la temperatura y velocidad sobre los materiales plásticos
3.1.2 Discretización
Una vez concluida la etapa de modelización debe realizarse la discretización, es decir, la división del medio continuo en elementos sencillos. Es en la generación de la malla de elementos donde mejor se aprecian las ayudas que el preprocesador suministra al usuario. Dichas ayudas van desde la generación de la misma por introducción de sus coordenadas hasta procedimientos totalmente automáticos.
Comúnmente es aceptado que una mayor densidad de división se corresponde con la obtención de mejores resultados. Si bien esto es así, existe la limitación del tiempo y capacidad de cálculo del ordenador que aumentan rápidamente conforme lo hace el número de nodos y elementos. La solución más acertada para un primer cálculo consiste en construir un mallado grueso para, en posteriores análisis, adaptarlo, esto es, hacerlo poco tupido en las zonas no comprometidas y fino en las zonas con gradientes importantes de las propiedades. En cualquier caso, no existe una discretización ideal: depende de su efectividad, de las particularidades de la pieza y de la experiencia del diseñador.
En la figura 6 se muestra la discretización definitiva de la carcasa. Se ha preferido una división en base a elementos triangulares puesto que en otro caso (malla de paralelepípedos) la topología compleja de las regiones a mallar implicaba operar con elementos muy deformados.
Figura 8 Valores de tensiones (MPa.)
3.1.3. Propiedades del material
La siguiente etapa del proceso es introducir las propiedades físicas del grado de polipropileno que se prevé utilizar. En el caso de materiales cuyo comportamiento puede considerarse básicamente lineal e isótropo basta con suministrar al programa características como densidad, módulo de elasticidad, coeficiente de Poisson, etc. Sin embargo, los plásticos, como consecuencia de su naturaleza viscoelástica, ven su comportamiento modificado por variables como la temperatura, velocidad de deformación y tiempo de aplicación de la tensión.
En la figura 7 se muestra el efecto de la temperatura y velocidad de deformación. Puede observarse que con el aumento de la temperatura disminuye el módulo elástico y la tensión de cedencia, aumentando la elongación a rotura. La velocidad por su parte tiene consecuencias opuestas.
No puede olvidarse la importante influencia del tiempo sobre los materiales plásticos que presentan fenómenos de fluencia y relajación de tensiones. Asimismo, la relación tensión-deformación es diferente según la pieza se encuentre traccionada o comprimida, y deberán aplicarse criterios diferentes en cada caso o utilizar los de tracción que son más conservadores.
La realidad puede complicarse todavía más si consideramos la anisotropía en la distribución de las fibras que, como en el caso de la carcasa, puede producirse en el interior del molde de inyección.
Todos los fenómenos anteriores se han tenido en cuenta en la modelización del ejemplo que nos ocupa. De la simulación de la inyección [3] se ha concluido la no existencia de orientaciones definidas en la distribución de la fibra. Por tanto, el material se ha considerado isotrópico y de módulo elástico ponderado por:
Ec = Módulo elástico del sistema fibra-matriz.
K1 = Factor de corrección según la orientación de las fibras.
Ef = Módulo elástico de la fibra.
Vf = Fracción en volumen de fibra.
Em= Módulo elástico de la matriz.
Para considerar el comportamiento del material se introduce la curva tensión-deformación y los datos para el polipropileno cargado con un 30% de fibra de vidrio, utilizándose los del Hostacom tipo G3 U01 de Hoechst [9].
3.1.4. Condiciones de entorno
El último paso antes de proceder al cálculo mecánico de la pieza es establecer sus condiciones de contorno, por consiguiente, las fuerzas o presiones actuantes sobre el cuerpo y también las restricciones o ligaduras que se oponen al libre desplazamiento del mismo.
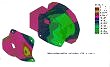Figura 9 Corriemientos axiales en el eje z (mm.)
Sobre la carcasa, las acciones exteriores son las efectuadas por la presión del agua al pasar por la bomba. Dicha presión se reparte uniformemente por toda la carcasa y su magnitud no supera los 0,3 MPa.
Las condiciones de ligadura impiden el desplazamiento relativo entre cabeza y cuerpo de la bomba en los cuatro puntos que se utilizan para unirlas. A continuación se restringe el desplazamiento y la rotación de los nodos correspondientes a la unión entre bomba y tubería. Esta unión se realiza a través de un inserto metálico de latón.
3.2. Procesado
El módulo de procesado es el encargado de resolver el sistema de ecuaciones resultado del anterior planteamiento físico. El programa que se utiliza permite realizar cálculos de muy diversas clases: estáticos, dinámicos, térmicos, vibratorios y otros.
El análisis que se lleva a cabo es de tipo estático. Se determinan los desplazamientos de los nodos consecuencia de la solicitación aplicada y posteriormente las tensiones y deformaciones de la pieza. El cálculo evaluará las condiciones de la pieza a tiempo de funcionamiento de 2 años (T=2 años).
3.3. Postprocesado
Los resultados del programa, al igual que los parámetros de entrada, son una serie de archivos que contienen numerosos datos. Sin una adecuada elaboración resulta prácticamente imposible extraer conclusiones válidas. El postprocesador recoge los datos de salida del programa y los transforma en gráficos que muestran los desplazamientos, tensiones y deformaciones de la pieza. También se extrae información muy útil de la comparación entre la figura inicial y la deformada y de la animación virtual del modelo. Con estos gráficos y animaciones se puede prever cuál será el comportamiento de la pieza y eventualmente detectar errores.
3.4. Resultados
El valor máximo de la tensión en la carcasa, con la bomba en funcionamiento y para las condiciones especificadas con anterioridad, resulta ser de 3,65 MPa (figura 8). Este valor se localiza a la entrada de la bomba y corresponde al lugar donde el fluido cambia de dirección y va hacia la tapa de salida. El valor obtenido está bastante por debajo del que puede resistir el tipo de polipropileno seleccionado al cabo de dos años de funcionamiento ininterrumpido.
La máxima separación entre cuerpo y tapa de la carcasa se da axialmente en la dirección del eje z, resultando ser de 0,11 mm (figura 9). Se puede asegurar, pues, que no se producirán fugas en servicio ya que esta separación es menor que la admisible (0,5 mm). Los valores de las deformaciones son prácticamente despreciables (del orden del 0,15%), por lo que no existirán deformaciones permanentes en la pieza.
Los resultados obtenidos en este estudio aseguran el buen comportamiento mecánico del Hostacom G3 U01 como material alternativo a la poliarilamida IXEF en la fabricación de la carcasa de la bomba periférica.
4. Ventajas y limitaciones de la simulación CAE
Las ventajas del uso de las herramientas CAE al diseño de piezas resultan evidentes. Su gran versatilidad permite resolver problemas de carácter multidisciplinar y gran complejidad con precisión ajustada y con conocimiento de la magnitud del error cometido en las aproximaciones.
No sólo proporcionan más y mejor información que los métodos tradicionales sino que se obtienen grandes ahorros en los costes y en el tiempo de desarrollo de los proyectos, lo que permite evaluar rápidamente cualquier modificación que se introduzca.
Del mayor acercamiento a la realidad se consiguen piezas más ajustadas y ahorro de material. Por otro lado, mediante la simulación numérica se obtiene un conocimiento detallado y profundo del producto antes de su existencia física y, bajo condiciones de funcionamiento extremas, se reduce en gran medida la posibilidad de que se produzcan problemas a posteriori.
El inconveniente más importante del método es la creencia absoluta en los datos que proporcionan los programas. Desde el momento en que es el usuario quien plantea correcta o incorrectamente el programa se debe ser crítico con los resultados y someterlos a una discusión exhaustiva antes de aceptarlos como válidos.
La conclusión final es que el método de los elementos finitos es una potente herramienta siempre que sea utilizada por manos expertas.
Nota: Los autores agradecen a la CICYT la financiación del proyecto MAT93-03431 en cuyo marco se ha realizado este trabajo.
