Límites actuales de la simulación numérica de los procesos de fabricación de plásticos y plásticos reforzados
Laboratoire de Mécanique des Systèmes et des Procédés (LMSP)01/02/2007
Actualmente puede, sin lugar a dudas, decirse que se ha alcanzado un gran dominio en lo que se refiere al diseño y utilización de los materiales compuestos en los que existe un control sobre la disposición del refuerzo. Por el contrario no existe todavía una experiencia clara y contrastada en lo que se refiere al diseño y fabricación de los materiales compuestos con refuerzo a base de fibras cortas. Las razones de este retraso son diversas, y entre ellas pueden considerarse las siguientes:
Las piezas con una finalidad fundamentalmente resistente son en general concebidas utilizando refuerzos en forma de tejidos, fibras continuas, ..., donde se obtiene un gran control en todos lo casos de su orientación durante el proceso de fabricación. De este modo se obtiene una gran reproductibilidad de los resultados, así como una predicción fiable del comportamiento mecánico.
En general, el campo de aplicación de los termoplásticos reforzados con fibras cortas se ha restringido a las aplicaciones con un nivel reducido de exigencias mecánicas. Ello ha sido sobre todo debido a la difícil predicción y control de la disposición (orientación) de las fibras en el producto conformado, obtenido en general mediante procesos de inyección, extrusión y termoformado, entre otros. En todos estos procesos pueden distinguirse dos fenómenos físicos: el flujo del material y la
evolución de la orientación de las fibras inmersas en él. Puede asimismo comprenderse que ambos fenómenos se hayan íntimamente acoplados, esto es, la existencia de las fibras y su orientación afectan al régimen del flujo, y es éste último quien a su vez gobierna la evolución de la orientación de las fibras. De este modo puede hablarse de una anisotropía inducida por el proceso de conformado.
Hoy en día los escenarios industriales evolucionan rápidamente, y comienza a percibirse un interés incipiente en el control de la disposición del refuerzo en materiales reforzados con fibras cortas. Este es el caso de todas las industrias que emplean termoplásticos reforzados, pero con la finalidad de aportar mayor concreción sobre el interés industrial, nos centraremos en las próximas líneas en un ejemplo bien conocido por los autores, relativo a la problemática del diseño en las industrias del sector del juguete.
La modelización de estos procesos deberá pues aportar soluciones a las cuestiones siguientes:
Dadas las condiciones del proceso, predecir la orientación final de las fibras en cada punto de la pieza.
Dado un estado de orientación de las fibras en la pieza, predecir el comportamiento mecánico cuando ésta sea sometida a las acciones de diseño.
La optimización mecánica puede abordarse mediante el control de la anisotropía inducida por el flujo, accesible mediante una adecuada modificación geométrica y/o de las condiciones y parámetros del proceso.
Actualmente la predicción precisa de la aniotropía inducida en piezas 3D no es posible mediante la utilización de programas de simulación comerciales. Consecuentemente la posibilidad de un control es un objetivo raramente planteado, al margen de casos extremadamente sencillos y por tanto alejados de nuestro interés. Estas limitaciones no se deben sólo a aspectos numéricos o de computación, sino que además existen numerosas limitaciones que afectan directamente a la modelización mecánica. Los habituales modelos mecánicos han sido desarrollados en el marco de la mecánica de los medios continuos, mediante el uso de técnicas de homogeneización para introducir la microestructura asociada a la orientación de las fibras. Estas modelizaciones hacen uso de no pocas hipótesis, muchas de ellas sensiblemente alejadas de la realidad industrial. En este caso se ha de suponer que los modelos mecánicos, fuera de las condiciones en que fueron deducidos, siguen siendo formalmente similares, si bien los parámetros involucrados deberan identificarse mediante una adecuada experimentación.
Este ha sido el contexto de nuestras actividades de investigación durante los últimos diez años.
Puesto que ni la problemática, ni la metodología, son exclusivas de la industria del plástico, las soluciones aportadas han sido extendidas a otros sectores con la misma problemática, como es la fabricación de estructuras con hormigón de alta resistencia reforzado con fibras cortas metálicas.
Anisotropia inducida por los procesos de conformado
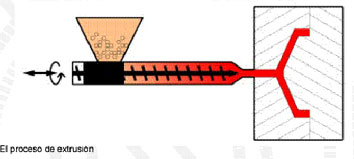
El proceso de inyección
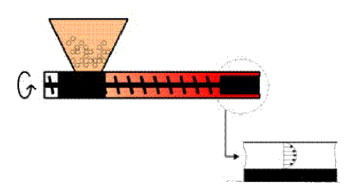
El proceso de extrusión
Análisis de la anisotropía inducida
• Un proceso de flujo de la suspensión que induce una orientación en las fibras.
• Una evolución en la orientación de las fibras que afecta a la cinemática del flujo.
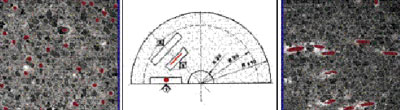
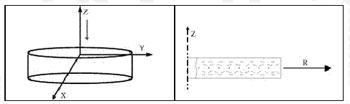
El primer fenómeno es intuitivo desde el punto de vista físico. Para ponerlo en evidencia supongamos que se inyecta un disco (Fig. 3-a), situando el punto de inyección en el centro geométrico de su base superior, con una suspensión de fibras muy alargadas (p.e. de longitud 0.1 mm y diámetro 0.001 mm). Si una vez conformada la pieza, se secciona por un plano definido por el eje del disco y un diámetro, y se observa al microscopio, se apreciará una clara evolución de la orientación de las fibras a través del espesor (Fig. 3-b). Así, en las proximidades de las bases del disco (paredes del molde) encontramos las fibras sensiblemente alineadas en la dirección radial (dirección del flujo durante el llenado del molde), mientras que en las proximidades del plano medio del molde las fibras quedan sensiblemente alineadas en la dirección circunferencial (perpendicularmente a la dirección del flujo durante llenado). En la transición entre estas zonas encontramos regiones donde las fibras se disponen de forma aleatoria, resultando un estado de orientación isótropo.

A partir de las conclusiones cualitativas obtenidas del análisis de los anteriores flujos simples, podemos tratar ahora de justificar la distribución de orientaciones obtenida durante el proceso de inyección del disco. Así, dadas las condiciones de adherencia del fluido al molde y la simetría del flujo respecto al plano medio, se tendrá un flujo fundamentalmente de cortadura cerca de las bases, mientras que en la vecindad del plano medio la cortadura será prácticamente despreciable frente al régimen de elongación inducido por el flujo radial. Ello justifica plenamente el haber encontrado las fibras sensiblemente alineadas con el flujo cerca de las bases y orientadas en la dirección circunferencial (perpendicular a la dirección del flujo) en las proximidades del plano medio. En las regiones de transición entre el régimen de elongación y el de cortadura las fibras quedarán orientadas aleatoriamente al no existir un carácter preferencial en el flujo.
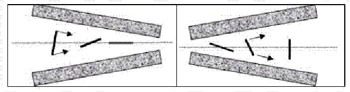
A continuación vamos a tratar de poner de manifiesto la dependencia inversa, esto es, que la presencia de las fibras, y su orientación, afectan a la cinemática del flujo.
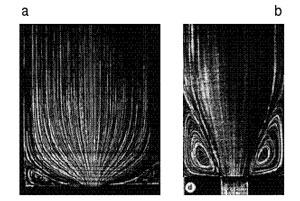
Para ello consideramos el flujo a través de una contracción capilar a muy bajos números de Reynolds (de modo que los efectos inerciales son despreciables frente a los efectos viscosos). Si suponemos la relación de diámetros en la contracción 4:1, en ausencia de fibras (y siendo el fluido newtoniano) las líneas de corriente del flujo se muestran en la figura Fig. 6-a. Se puede apreciar una recirculación de tamaño muy reducido en las inmediaciones de la esquina de la contracción. Este resultado experimental es perfectamente previsible a partir de la resolución del problema de Stokes que gobierna el flujo.
Por el contrario cuando al fluido se le agrega una cierta cantidad de fibras cortas (aun manteniendo la concentración de estas inferior al 1 por ciento) el régimen del flujo cambia drásticamente según se aprecia en la figura Fig. 6-b. Con este ejemplo hemos puesto asimismo de manifiesto que la existencia de fibras en suspensión afecta sensiblemente al régimen del flujo.
Hacia una previsión de la anisotropía inducida
Podría pensarse que una posible solución consistiría en la determinación experimental de la orientación de las fibras en un prototipo. Sin embargo esta posibilidad no resulta factible en la práctica por cuanto (i) entraña un coste elevado, (ii) precisa de un tiempo considerable, (iii) no es compatible con un diseño automatizado, y (iv) hace prohibitiva cualquier estrategia de optimización.
Por todo ello se impone una adecuada modelización mecánica y numérica a fin de poder resolver el modelo acoplado flujo-orientación de las fibras, y poder así simular numéricamente el estado final de la orientación de las fibras y con ello establecer previsiones sobre el comportamiento mecánico de la pieza en servicio. El estado actual de las investigaciones en este campo abordan el establecimiento de esta modelización mecánico-numérica, la propuesta de ensayos aptos para la identificación de los parámetros involucrados en el modelo así como para la validación experimental de las predicciones numéricas obtenidas.
Hacia un control de la anisotropía inducida
Si el perfil tubular estuviera sometido en servicio a solicitaciones de tipo traccion-flexion, podriamos concluir que el propio proceso de fabricación ha inducido en la pieza una adecuada anisotropía (fibras orientadas en la dirección de las tensiones normales). Por el contrario si suponemos que la pieza va a estar sometida en servicio a presiones internas, entonces podremos afirmar que el proceso de fabricación ha inducido una anisotropía con escasa incidencia sobre las propiedades mecánicas de la pieza en servicio.
La cuestión que se impone es saber si se puede diseñar una boquilla en vistas a alinear las fibras precisamente en la dirección circunferencial (más adecuada desde el punto de vista resistente a la presión interna). La respuesta a esta cuestión entra de lleno en la temática del control de la anisotropía inducida.
Modelado numérico
Esta homogeneización se lleva a cabo asumiendo diferentes hipótesis, entre ellas el carácter newtoniano del fluido matriz (en el cual se hayan inmersas las fibras) y la ausencia de interacciones de contacto entre las fibras. Ambas hipótesis alejan claramente el marco de la modelización, del ámbito de su aplicación industrial, que opera con termoplásticos con un marcado carácter no newtoniano y concentraciones de fibras de hasta el treinta por ciento en volumen, muy por encima del límite de validez de los desarrollos teóricos. En este caso asumiremos tácitamente que los modelos a aplicar son formalmente idénticos, si bien todos los parámetros involucrados deberán determinarse mediante una adecuada experimentación.
Respecto a la identificación experimental de los parámetros reológicos involucrados en la ecuación constitutiva, para regímenes de concentración como los encontrados en las aplicaciones industriales, existen pocos precedentes.
En lo que respecta a la segunda modelización, de carácter fundamentalmente numérico, existen antecedentes de discretizaciones 2D, 2D-axisimétrica, 3D-placa (geometrías tridimensionales con una dimensión -el espesor- muy reducida frente al resto de dimensiones representativas de la pieza, y que permiten importantes simplificaciones en su tratamiento numérico). Este último caso es de un gran interés industrial puesto que numerosas piezas pueden considerarse como el ensamblado de placas y/o laminas. Actualmente existen diferentes programas de simulación comerciales capaces de simular el llenado de moldes de reducido espesor, y predecir el estado final de orientación de las fibras. Las predicciones numéricas han sido ampliamente contrastadas con los resultados experimentales, siendo en general los resultados satisfactorios.
Recientemente son numerosas las aplicaciones que requieren pequeñas piezas de geometría compleja que no pueden ser consideradas como un ensamblado de placas y/o láminas. En este caso la única solucion factible pasa por una verdadera modelización tridimensional. En la actualidad no existe ningún programa comercial que efectue este tipo de simulaciones, si bien son numerosos los grupos que en la actualidad trabajan en su desarrollo, por lo que se puede afirmar que previsiblemente en breve existirán diferentes prototipos comerciales disponibles.
Aportaciones científicas significativas de los autores
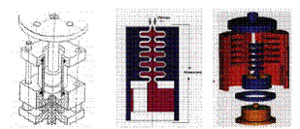
• Proponer nuevas estrategias numéricas adaptadas al tratamiento numérico del modelo acoplado flujo-orientación.
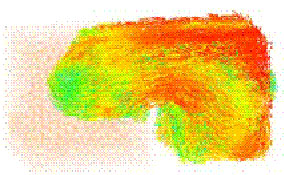
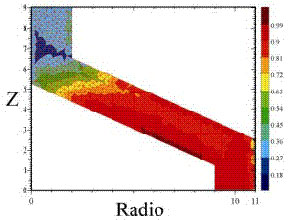
• Elaborar un programa de simulación 3D para el conformado de termoplásticos reforzados con fibras cortas. Un ejemplo de simulación de llenado de un molde se presenta en la figura 8. En la figura 9 se ilustra la orientacion más probable de las fibras en un determinado instante del proceso de inyeccion. En esta figura el vector denota la direccion de orientacion de las fibras más probable en cada punto, y su longitud (color) la magnitud de dicha probabilidad.