Obtención automática de un modelo sólido a partir de una perspectiva bocetada

Este trabajo ha sido desarrollado como parte de una aplicación que permite la obtención de modelos tridimensionales a partir de bocetos que representan una perspectiva del modelo. El boceto es realizado mediante una tableta gráfica LCD, donde el usuario va esbozando su diseño que mediante un proceso de reconstrucción 2D permite de forma automática el reconocimiento de la entidad dibujada y su ajuste inteligente con las entidades que se muestren próximas a ella. La acción de borrar es tan sencilla como rayar las entidades que deseamos eliminar.

En la actualidad nuestra aplicación exporta el modelo de superficies en formato DXF y VRML [3]. El objetivo de este trabajo es generar, a partir del modelo de superficies un modelo sólido B-rep permitiendo generar un formato STEP (ISO 10303) para permitir su reutilización en otras aplicaciones CAD. Para este último paso se ha elegido el protocolo de aplicación 203, que en la actualidad está presente en la mayor parte de las aplicaciones CAD comerciales.

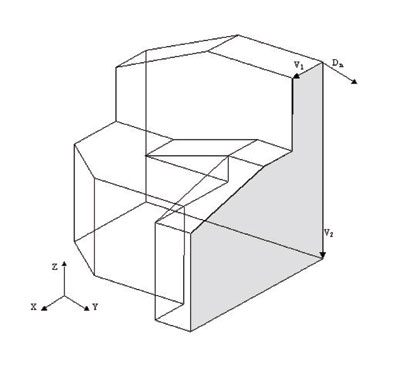
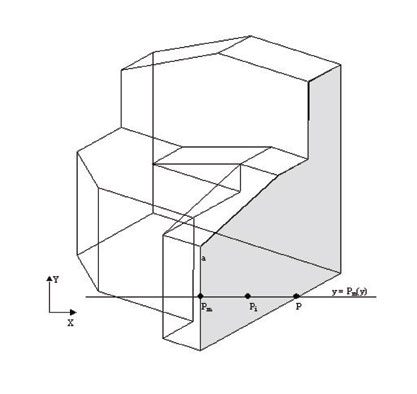
• Entre todos los vértices de la cara seleccionamos aquel que, no perteneciendo a ninguna arista horizontal, tenga menor coordenada “x” en la proyección de la imagen.
• Tomamos una arista de la cara que concurra en dicho vértice (a) y obtenemos su punto medio Pm (x,y).
• Obtenemos el punto (P) de menor coordenada “x” de las intersecciones de la recta definida en la forma y = Pm(y) con el resto de las aristas de la cara.
• Se define como punto interior a la cara (Pi), el punto medio de Pm y P.

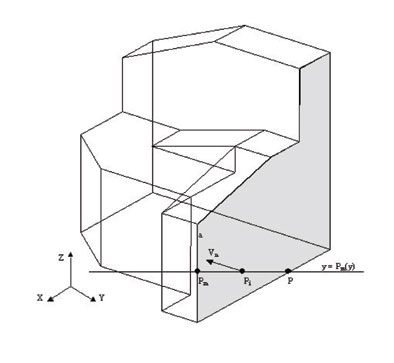
Determinado el vector normal a la cara queda por comprobar si su sentido apunta hacia el exterior del modelo. Tal evaluación se realiza de acuerdo con el siguiente algoritmo:

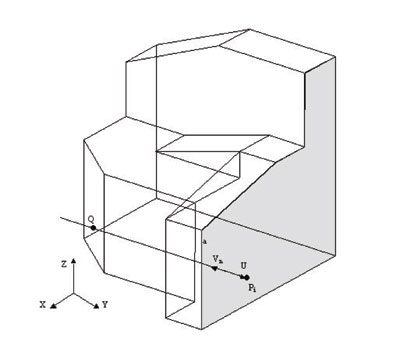
• Determinamos la arista definida por el punto interior y el vector normal al plano de la cara del modelo.
• Obtenemos los puntos de intersección de dicha arista con el resto de las caras definidas en el modelo (Q).
• Determinamos los vectores definidos por los puntos de intersección y el punto interior de la cara, de manera que: si el número de dichos vectores que tienen el mismo sentido que el vector V es par o nulo, se modifica el sentido del vector normal.

Una vez conocidas las orientaciones del vector normal de cada cara, se dispone de la información necesaria para generar un modelo B-rep que represente al sólido, utilizando el formato STEP [3].

Para ello se ha utilizando la entidad Manifold_Solid_ Brep la cual queda definida a través de la entidad Closed Shell. Ésta última sirve como frontera para una región finita del espacio R3 que está definida por una colección de caras orientadas.

En nuestro caso, estas caras, son superficies planas por lo que puede utilizarse en su definición otra entidad denominada, Poly_Loop , compuesta por una lista ordenada de los vértices que componen cada una de las caras. (El orden en el que se recorren es indiferente). Estos recorridos cerrados se asocian a las entidades Face_Bound y Face_Surface, que nos permiten definir la orientación de la cara, mediante el uso de la cadena “.T.” o “.F.” para designar si el recorrido de los vértices en cada cara es coherente con el sentido del vector normal (True) o es opuesto (False). El contenido de parte del fichero STEP según la definición de la parte 21 tendría el siguiente aspecto:

• #33=POLY_LOOP((#3,#4,#1,#2));.
• #39=FACE_BOUND(#33,.T.);
• #40=FACE_SURFACE((#39),#27,.F.);
• #51=CLOSED_SHELL((#40,#42,#44,#46,#48,#50));
• #52=MANIFOLD_SOLID_BREP(#51);