Requisito fundamental para la inspección geométrica de piezas industriales

El diseño actual de la mayoría de las piezas industriales se realiza con la ayuda de los sistemas CAD de modelado tridimensional. El resultado de un modelado geométrico de pieza es un fichero informático. A partir de este se elaboran los planos con la definición explícita de la pieza incluyendo, vistas, cortes, detalles, elementos de acotación, tolerancias geométricas y dimensionales, especificaciones de acabado de superficies etc. La valoración de la magnitud real de las especificaciones geométricas de definición es fundamental para la homologación de los procesos de fabricación. A continuación se pretende realizar una aproximación a la problemática del proceso de medición, precisamente a la fase de alineación de piezas, debido a la importancia que tiene esta en la obtención de resultados de confianza

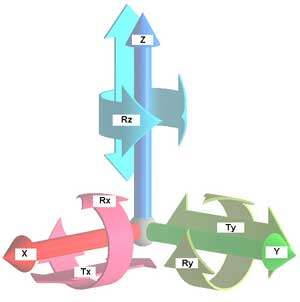
El análisis geométrico de piezas complejas se realiza con la ayuda de las máquinas de medir tridimensionales. Para iniciar este proceso es necesario fijar la muestra representativa en el entorno de trabajo de la máquina. Se pretende conseguir así el bloqueo de todos y cada uno de los seis grados de libertad que tiene la pieza en el espacio.

Figura 1 Grados de libertad

Figura 2 Pieza en inspección sobre útil de fijación

Para piezas definitivas a producir en miles de unidades se dispone normalmente de un útil de verificación. Se trata de un artefacto mecánico que asegura rigidez, accesibilidad y repetibilidad. Esto significa que las piezas de poco grosor van a ganar la consistencia necesaria para la exploración por contacto discreto; la forma y la orientación del útil permiten acceder de una sola estacada a todas las zonas de interés y durante el proceso de "pone/quita" de la pieza no se genera ningún error geométrico. Sobre estos útiles se definen y se marcan elementos de referencia que ayudan a crear el sistema de coordenadas necesario para la inspección.

Figura 3. Útil de fijación RAPID FIT

Estos útiles suelen ser caros y para las piezas en fases de desarrollo o de series pequeñas no son disponibles.

Para estos casos son preferibles los útiles de fijación de bajo coste que se consiguen a corto plazo. En el Departamento de Metrología de la Fundación ASCAMM proponemos la solución RAPID FIT. Este sistema ofrece la posibilidad de construir columnas de apoyo y fijación , que conectan la pieza con una base de fijación de estructura modular. En estas columnas, la zonas de apoyo para la pieza se consigue mediante técnicas de rapad prototiping, utilizando el modelo CAD de esta. Un ejemplo se puede ver en la Figura 3.

Figura 4. Útil de fijación modular sobre AIRBASE

También disponemos de un conjunto de útiles de fijación de estructura modular en cuya composición entran: bases de fijación sobre cojín de aire, articulaciones esféricas con tres giros perpendiculares, mordazas, plataformas etc que ofrece la posibilidad de construir fijaciones con muy buena repetibilidad y accesibilidad. Una composición de estos elementos modulares se puede ver en la Figura 4.

Existen normas como ISO 1101 - 1983 o ASME Y 14.5M-1994 que recomiendan como se deben alinear las piezas industriales. Las normas asignan al diseñador de la pieza la responsabilidad de definir el sistema de referencia, mediante características representativas y restricciones sobre estas. Tal información se va a reflejar en los planos, mediante una simbología, cuya lectura e interpretación permiten al metrólogo reproducir el razonamiento del diseñador.

¿Es posible alinear por sólo tres puntos? Encontrar respuesta a esta pregunta ha sido un reto importante para los programadores de software de medición geométrica

Figura 5. Definición gráfica de elementos de referencia

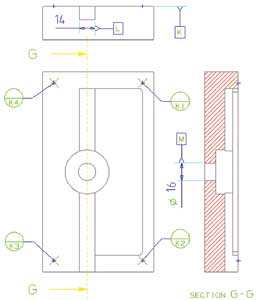
En este método se implica la característica más representativa para bloquear 3 de los grados de libertad. Lo más habitual es utilizar para este propósito un plano. Seguidamente se explora una línea, situada o proyectada sobre el plano anterior, mediante la cual se pueden bloquear otros 2 grados de libertad. Hay que remarcar que el incumplimiento de las exigencias de forma (planicidad, rectitud) descalifica las características en atención para su uso en alineación. Finalmente solo falta 1 punto para bloquear el último grado de libertad del sistema de coordenadas. Si alguna de las características implicadas en alineación incumple exigencias de forma es necesario, antes de seguir, consultar al beneficiario de la pieza para encontrar una solución alternativa. También se pueden implicar en procesos de alineación otras primitivas geométricas como: cilindros, conos, ranuras, toros o superficies parabólicas. A la característica más comprometida la llamamos, datum primarium. Esta define el primer eje del sistema de referencia. El segundo eje lo define la característica que llamamos datum secundarium. El tercer eje es implícito, siendo perpendicular al plano definido por los anteriores dos ejes. El origen del sistema de coordenadas lo define la característica que llamamos datum terciarium. Los elementos de referencia se ven señaladas con las letras K, L, M en la Figura 5.

El orden alfabético de las letras con las que se señalan los elementos de referencia corresponde con el orden de importancia de estos en la definición del sistema de coordenadas, siendo la letra mas alta la que corresponde al datum primarium.

En este proceso el software de medición calcula la matriz de transformación que resulta al relacionar unos puntos representativos, medidos sobre la pieza con sus respectivas coordenadas teóricas.

Tras la primera transformación se procede a iteraciones en las cuales se vuelven a medir los mismos puntos en el nuevo sistema de coordenadas para conseguir una alineación más acertada, procurando minimizar las desviaciones de los puntos. Señalamos que no siempre este método converge hacía resultados mejorados. Además ninguno de los puntos resulta plenamente colocado. La repetibilidad del método es baja. No obstante se utiliza para la evaluación de la calidad de las superficies libres en las cuales los puntos de anclajes definitivos no están decididos.

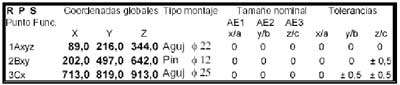
T1 Tabla de restricciones RPS

¿Es posible alinear por sólo tres puntos? Encontrar respuesta a esta pregunta ha sido un reto importante para los programadores de software de medición geométrica. En algunos de estos existe implementada una función que cumple esta necesidad. Los constructores de automóviles requieren que en el proceso de alineación se asegure el bloqueo de los grados de libertad de piezas individuales o conjuntos de forma similar al proceso de montaje que se realiza con la ayuda de la robótica industrial. Estos requerimientos se expresan en tablas RPS que marcan la tolerancia de posicionamiento admisible para los puntos representativos implicados en el montaje.

Aquellas coordenadas que tienen valor "0" para la tolerancia de posición cumplirán obligatoriamente el valor nominal, mientras que las otras podrían oscilar dentro del campo de tolerancia asignado. La tabla T1 presenta un ejemplo de restricciones RPS para los puntos de nombre A, B y C. Se puede remarcar una similitud con el anterior método 3, 2, 1. A los tres puntos se les bloquea la coordenada x. Esto significa conseguir el primer eje como dirección X. Los puntos A y B, obligados a cumplir las coordenadas en y van a definir el segundo eje como dirección Z, perpendicular al anterior. El punto A, el más comprometido va a definir mediante dimensiones básicas el origen del sistema de coordenadas. Hay que señalar que los puntos que se implican en este proceso de alineación tienen que ser centros de primitivas geométricas de confianza como: esferas, colisos, ranuras, toroides etc.

En el Laboratorio de Metrología dimensional de la Fundación ASCAMM se ha desarrollado un programa capaz de dar respuesta a este problema. Se trata de un modulo de calculo escrito en formato ".xls " de Microsoft Excel que permite una continua interacción con el usuario. Para empezar se tienen que llenar las zonas de las coordenadas nominales y reales de los puntos A, B, C. Para cada uno se marcan las restricciones y las libertades, según la tabla RPS. Con símbolo "0" se ven marcadas en la tabla T2 las obligaciones y con "1" las libertades.

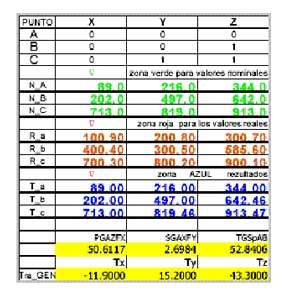
T2 Tabla de cálculo de transformaciones

En el mismo libro Excel, a continuación a la hoja principal, hay 21 hojas más que calculan todas las versiones que se pueden imaginar a partir de los datos y las restricciones de entrada. El sistema señala las soluciones imposibles, las situaciones particulares (puntos colineares, puntos muy dispersos etc.) y si procede recomienda cambios en la tabla de restricciones, para minimizar los errores de posición de los puntos B y C. Estos disponen de libertades en uno y respectivamente en dos de los ejes, mientras que el punto A, que es el más restringido, siempre cumple las tres coordenadas. Al final el programa ofrece la magnitud de los tres traslados y los tres giros necesarios para solapar los puntos reales con los nominales en el sistema de referencia deseado. También se realiza una comparación entre las distancias nominales y las distancias reales, constatadas entre los puntos analizados. Si en una pieza de plástico se constata que todas estas distancias están mas cortas o más largas de lo previsto, estamos en el caso de un error debido al uso de un material con el coeficiente de contracción inapropiado. Si se constatan que dos de estas distancias resultan más pequeñas y la tercera es más grande de lo previsto estamos en el caso de una pieza retorcida. Al no depender de ningún software de medición, este programa puede ofrecer una solución rápida a problemas de alineación en metrología, a problemas de solape de puntos digitalizados sobre superficies en distintos sistemas de referencia, a problemas de cálculo de posiciones en robótica. Su formato tan popular lo hace asequible a multitud de usuarios.