IK4-Tekniker ha desarrollado un modelo teórico que simula conjuntamente la dinámica de la estructura, accionamientos y lazos de control de una máquina-herramienta
Desarrollo de una máquina virtual para el análisis dinámico de máquinas-herramienta de gran tamaño
IK4-Tekniker ha desarrollado un modelo teórico en el que se engloban las capacidades dinámicas de las máquinas-herramienta, tanto estructurales como de los accionamientos, y el efecto de la configuración de los lazos de control. Esta ‘Máquina Virtual’ permite analizar el comportamiento dinámico de la máquina en su conjunto pudiendo realizar los mismos ensayos que se realizan en las puestas a punto: posicionamientos, escalones de posición/velocidad, pruebas de circunferencia, etc. En este trabajo se muestra la validación del modelo con dos aplicaciones distintas. La ‘Máquina Virtual’ facilita la realización de un proceso iterativo de diseño en el que se pueda verificar el efecto de modificaciones de una manera sencilla.
1. Introducción
Hoy en día, la competencia del mercado globalizado requiere reducciones en el costo y en el tiempo de desarrollo de las máquinas. Además, los fabricantes de máquina-herramienta ya no pueden permitirse la fabricación y ensayo de prototipos físicos para poder detectar puntos débiles y, en base a ellos, realizar la optimización del diseño. La globalización de los mercados ha llevado a estas empresas a especializarse principalmente en dos familias de productos: máquinas especiales (principalmente para la industria del automóvil) y grandes máquinas para la energía eólica o la industria aeronáutica. Ambas familias de productos se caracterizan porque pocas veces dos máquinas son iguales y, prácticamente, se realiza un nuevo diseño en cada máquina producida.
En general, estas máquinas tienen cinemática cartesiana y accionamientos con husillo de bolas o piñón-cremallera. Durante el proceso de diseño es habitual realizar un análisis de Elementos Finitos empleando un software como MSCNASTRAN y durante ese proceso se suele realizar la optimización dinámica y estática de la parte estructural de la máquina. Este análisis no contempla la interacción de la estructura con el accionamiento/control, y para diseñar máquinas con gran ancho de banda, generalmente requeridos en la industria de automoción, es necesario tener en cuenta dicha relación. Otro de los campos donde es necesario tener en cuenta esta interacción es en el campo de las máquinas de gran tamaño donde las fuerzas de corte pueden ser de gran magnitud y las máquinas pueden verse afectadas por problemas de chatter. Por todo esto, es importante analizar el amortiguamiento que puede dar el sistema de control a cada modo de vibración, por lo que, es necesario realizar un modelo completo de la máquina donde se tengan en cuenta de forma conjunta tanto el control, como los accionamientos y la estructura. Este tipo de modelo se conoce como máquina virtual [1].
IK4-Tekniker ha desarrollado un modelo teórico que simula conjuntamente la dinámica de la estructura, accionamientos y lazos de control de una máquina-herramienta. Primeramente se describe el modelo realizado y, seguidamente, se validará mediante dos aplicaciones diferentes.
2. Descripción del modelo
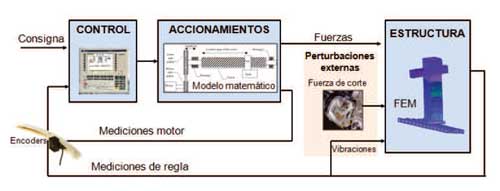
La Figura 1 muestra un esquema del modelo realizado integrando el control los accionamientos y la estructura de la máquina a analizar. El modelo se ha integrado en un entorno Matlab/Simulink. Para analizar el comportamiento teórico de una máquina se puede estudiar su respuesta frente a una consigna y/o frente a perturbaciones externas (fuerzas de corte y rozamiento). En el caso de querer analizar el comportamiento de la máquina ante una trayectoria real, se puede obtener la misma a partir de ficheros de código G y alimentar el modelo con ella. A continuación se describe cada bloque del modelo por separado.
2.1 Control
El bloque de control diseñado contiene los lazos habituales en aplicaciones motion control: un lazo de posición proporcional (P) y un lazo de velocidad proporciona-integral (PI). El lazo de corriente se considera ideal. Además de esto, existe la posibilidad de activar el feedforward tanto de velocidad como de aceleración. Este es un algoritmo general, sin embargo, existe la posibilidad de adaptarlo a casos especiales. La salida de este bloque es el par del motor que se introduce en el bloque de accionamiento.
2.2 Accionamientos
Se emplean unos modelos dinámicos de varios grados de libertad para los accionamientos desarrollados por IK4-Tekniker [2]. Existen modelos para los tres tipos de accionamientos más habituales: husillo giratorio, tuerca giratoria y piñón-cremallera. Estos se han realizado empleando modelos de parámetros concentrados, donde se obtiene las matrices de masa y rigidez a partir de las ecuaciones de energía o Lagrangianas. Los datos de entrada de estos modelos serán las geometrías, masas, inercias y rigideces de los elementos del accionamiento (casi todos los datos se obtienen de los catálogos). Con las matrices de masa [M] y rigidez [K] se obtiene un sistema de espacio estado que se implementa en el modelo global. Como ejemplo, en la siguiente figura se pueden observar los grados de libertad que se han considerado en el caso del husillo giratorio. A este bloque le llega la señal de salida del bloque de control (Par del motor) y se obtienen las fuerzas transmitidas a la estructura.
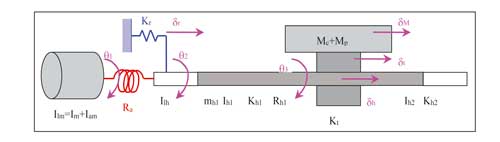
2.3 Estructura
La parte estructural se modeliza usando los resultados obtenidos en el cálculo realizado mediante elementos finitos (MEF), en los puntos de interacción con el bloque de accionamientos, en los que se hacen las medidas para alimentar el control y en el resto de puntos de interés como, por ejemplo, punta de herramienta. Este último análisis no es posible en una máquina real sin emplear material específico. Las entradas de este bloque son las fuerzas generadas en el bloque de accionamientos y la salida de este bloque son velocidades y desplazamientos de los puntos que se han tenido en cuenta en la estructura.
3. Validación con datos experimentales
A continuación, se van a analizar dos casos en los que se ha aplicado el modelo teórico y se han realizado validaciones del mismo mediante mediciones experimentales.
3.1 Ejemplo 1: Eje X de Fresadora de puente móvil
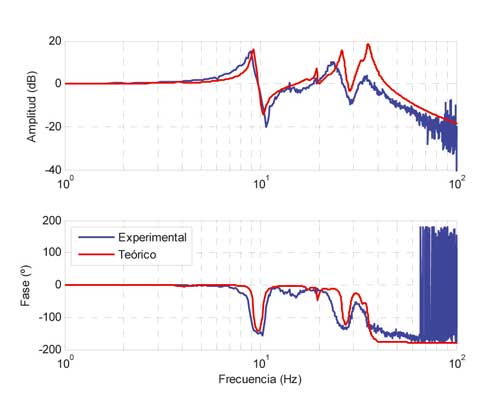
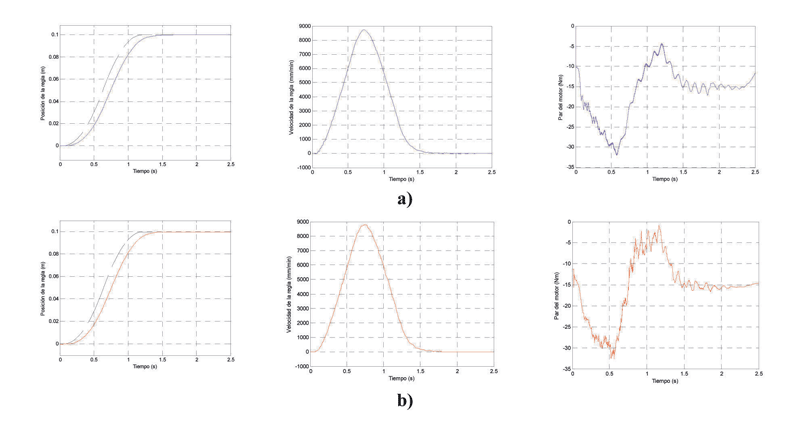
El movimiento del puente de la fresadora estudiada se realiza mediante un sistema Gantry compuesto por dos accionamientos de piñón-cremallera (uno en cada columna). El modelo desarrollado integra estos dos accionamientos (así, como sus correspondientes controles) y un modelo teórico de elementos finitos (MEF) de la parte estructural de la máquina. La Figura 3 muestra el diagrama de Bode entre la velocidad de la regla y la velocidad del motor tanto para el caso teórico como el experimental. El modelo desarrollado capta los tres modos principales de manera correcta. En la Figura 4 se muestran los resultados al realizar el mismo posicionamiento con el modelo y la máquina real. La correlación entre los resultados obtenidos con ambos sistemas es buena. Al emplear la misma configuración de control en el modelo y en la máquina se observa la excitación del primer modo en ambas señales de par. Existen algunas diferencias en las gráficas del par motor que son achacables a errores de modelizado de la fricción de las guías, que en este tipo de máquinas suele ser importante.
3.2 Ejemplo 2: Eje C de torno
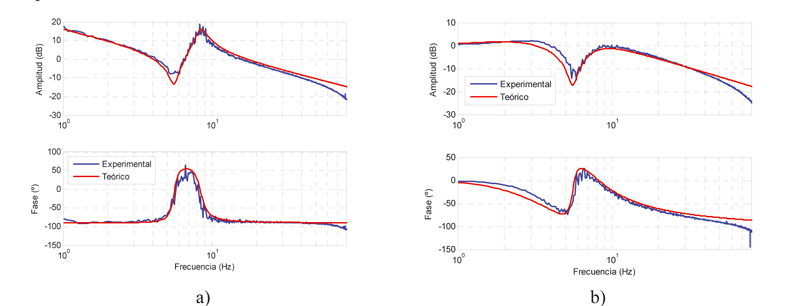
Se ha modelizado el comportamiento del eje C de un torno de grandes dimensiones (tamaño máximo de pieza Ø1.500x1.000 mm o Ø500x5.000 mm). En este caso, no se tiene en cuenta la parte de la estructura de la máquina, ya que se quiere centrar en el comportamiento dinámico del eje C y este tiene una influencia despreciable en la estructura. Así, el modelo consiste en una parte de control y otra de un accionamiento desarrollado específicamente en el que se modeliza el eje C, que consiste en un motor que mueve el plato/pieza a través un reductor comercial y un tren de engranajes, mediante parámetros concentrados. A continuación se compara el diagrama de Bode de lazo abierto entre velocidad y par motor, donde se observa la dinámica del sistema mecánico (Figura 5a). En ambos casos se observa con claridad la existencia de un modo dominante a 5,5/8,5 Hz. El modelo teórico permitió identificar que este modo provenía de una flexibilidad localizada en uno de los ejes del tren de engranajes. Al analizar el diagrama de Bode en lazo cerrado entre velocidad motor y velocidad consigna (Figura 5b), donde entra en juego el lazo de control, se puede observar que el resultado obtenido con el modelo teórico es muy similar al obtenido de forma experimental.
Este tipo de modelos puede ser muy útil ya que los cabezales cada vez tienen que soportar piezas de mayor tamaño y con un modelo de este tipo se puede tener en cuenta la respuesta del cabezal para diferentes tamaños de pieza sin tener que montarlas en máquina. Así, se podría definir el rango de tamaño pieza que la máquina será capaz de mover y la configuración de los lazos de control para que su dinámica sea aceptable.
4. Conclusiones
Se ha presentado un modelo teórico para analizar dinámicamente máquinas-herramientas que engloba control, accionamientos y la parte estructural de las mismas. Se han mostrado dos aplicaciones en el que el modelo replica con fidelidad la respuesta de las máquinas reales modelizadas. El modelo permite analizar la respuesta de máquinas frente a consignas simples, como escalones o posicionamientos, o más complejas, como trayectorias generadas mediante código G. También se puede estudiar el efecto de fuerzas de perturbación, como esfuerzos de corte o fricción.
Este modelo permite la realización de un proceso de diseño en el que se pueden analizar el efecto de las modificaciones en la dinámica sin necesidad de fabricar prototipos. Asimismo, se puede estudiar la dinámica de puntos que en la realidad no son fáciles de medir pero que son de vital importancia en los procesos productivos (punta de la herramienta). Estas ventajas se acentúan en máquinas grandes donde los costes de prototipado y disponibilidad son especialmente restrictivos.
Referencias
[1] Altintas Y, Brecher C, Weck M, Witt S, T.A; “Virtual Machine tool”; In: Annals of the Cirp, Turkey, Aug, 21-27 TC M, 54/2/2005
[2] Egaña F, Ruiz I, Zatarain M, Azpeitia J, T.A; “Simulación de accionamientos en máquina-herramienta y validación experimental”; En XIV Congreso de MH, Tecnologías de Fabricación, San Sebastian, 2002, p 761