Diseño, modelado geométrico y ensayo de una articulación
para un brazo medidor por coordenadas

En el presente artículo se muestra el proceso de diseño, modelado geométrico y ensayo de una articulación para un brazo medidor de coordenadas. El principal objetivo de este trabajo es servir de punto de inicio para un desarrollo futuro de brazos de medida tanto de propósito general como de aplicación concreta. De este modo, lo aprendido en el desarrollo del modelo geométrico de una articulación es de gran utilidad a la hora de una aplicación posterior a un brazo completo. Por otro lado, se ha desarrollado un procedimiento de optimización de parámetros geométricos que puede ser de gran utilidad de cara al desarrollo de procedimientos de calibración de este tipo de sistemas.

El presente trabajo muestra el desarrollo de una articulación para un brazo de medición por coordenadas. Este instrumento de manejo manual proporciona las coordenadas cartesianas de los puntos medidos con respecto a un sistema de referencia fijo.

Las ventajas principales de dicho brazo frente a otros sistemas son su facilidad de manejo, su gran flexibilidad de movimientos, su carácter portátil y su menor tamaño, lo que permite realizar mediciones rápidas sin apenas interferir en otros procesos que se estén llevando a cabo. Este sistema también permite la medición de piezas in situ sin necesidad de tener que trasladarlas al lugar donde se encuentre el instrumento de medición, como sí que ocurre, por ejemplo, con las máquinas de medición por coordenadas (MMC)

El brazo de medida puede poseer múltiples aplicaciones en sectores muy diversos y puede servir de base, mediante pequeñas modificaciones, a dispositivos similares de aplicación más específica. Así, mediante el diseño, la fabricación y el ensayo de una articulación, se pretende conocer la manera de modelar geométricamente este tipo de sistemas, así como determinar sus posibles mecanismos de error. Todo ello orientado a un posible desarrollo futuro de brazos de medida tanto de propósito general como para aplicaciones concretas.

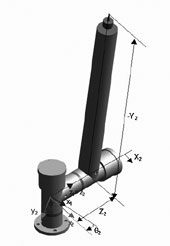
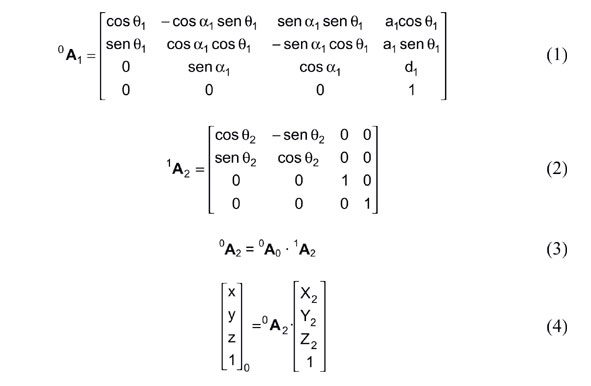
Una parte fundamental del proceso es la implementación del modelo geométrico necesario para transformar las lecturas obtenidas por los sensores en las coordenadas cartesianas del punto medido. Para ello se ha utilizado el método de representación de Denavit-Hartenberg [1] que permite sistematizar el cálculo de las matrices de transformación necesarias.

Por otro lado, se ha desarrollado un procedimiento de optimización de parámetros geométricos orientado a la corrección de los posibles errores de fabricación, de montaje o debidos a otras magnitudes de influencia.

La articulación que se diseña ha de servir de base a un posible desarrollo posterior de un brazo completo de propósito general de seis grados de libertad. Por ello, se decide dotar a dicha articulación de dos grados de libertad. De este modo, simplemente repitiéndola el número necesario de veces se conseguiría el número de grados de libertad deseado.

Se decide que los grados de libertad permitirán un giro con respecto a un eje vertical y otro con respecto a un eje horizontal que se producirán mediante la actuación de rodamientos angulares. Se diseña un sistema de limitación del giro a 720º para no permitir a cada uno de los ejes girar más de dos vueltas completas. Los sensores utilizados para la medición de los giros son encoders angulares de gran número de pasos para obtener una buena resolución en el sistema. El paso de los cables a lo largo de toda la estructura también se tiene en cuenta en el diseño, sobre todo de las carcasas.

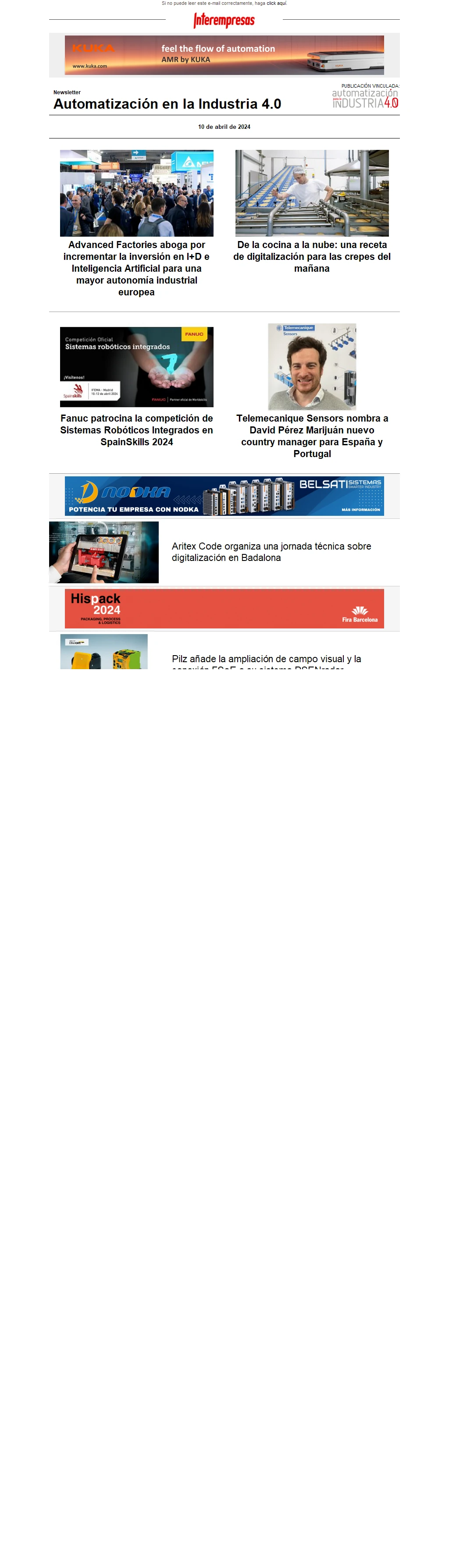
El aspecto externo de la articulación se puede observar en la figura 1. En ella se muestran los cuerpos vertical y horizontal con sus respectivas zonas de alojamiento de los encoders. En el diseño de la articulación se añadió un brazo con una esfera palpadora en su extremo que se utilizó en la fase de ensayo

Figura 1. Aspecto final de la articulación

Una vez diseñada la articulación y conocidos sus parámetros geométricos es necesario establecer un procedimiento para, a partir de dichos parámetros y de las lecturas de los sensores, conocer la posición de la esfera palpadora en cualquier momento con respecto a un sistema de referencia fijo. Para ello se realiza un modelo geométrico del sistema mediante el método de representación de Denavit-Hartenberg [1]. Este método, habitualmente utilizado en robótica, establece unos criterios de ubicación de sistemas de referencia intermedios en las articulaciones y de implementación de las matrices de transformación entre ellos. De este modo, las coordenadas de la esfera palpadora con respecto a un sistema solidario a ella se transformarán mediante rotaciones (donde las lecturas de los sensores son fundamentales) y traslaciones hasta un sistema de referencia fijo que, en este caso, se ha ubicado en el centro de su base.

En la figura 2 se muestra la ubicación de los distintos sistemas de referencia y los parámetros geométricos necesarios para las transformaciones. El sistema de referencia 0 es el que se considera la referencia fija. El sistema 1 gira solidario al eje vertical, por lo que los valores de q1 vendrán dados por las lecturas del encoder que mide ese giro. Del mismo modo, los valores de q2 vendrán dados por las lecturas del encoder que mide el giro con respecto al eje horizontal, eje al cual es solidario el sistema 2.

Figura 2. Sistemas de referencia y parámetros utilizados en el modelo geométrico

Las matrices de transformación entre sistemas se muestran en las siguientes ecuaciones:

La ecuación (1) representa la matriz de transformación entre el sistema 1 y el 0. La matriz de cambio del sistema 2 al 1 se muestra en la ecuación (2). La ecuación (3) indica el modo en el que las matrices anteriores han de combinarse para obtener la matriz global de cambio del sistema 2 al 0. Por último, en la ecuación (4) aparece el modo de transformar las coordenadas X2, Y2 y Z2 a coordenadas con respecto al sistema 0 o sistema fijo. Los parámetros a1, d1 y a1, al igual que X2, Y2 y Z2, se obtienen por medición directa de la geometría de la articulación.

Para la medición de los parámetros geométricos necesarios en el modelo se utiliza una máquina de medición por coordenadas (MMC). Por otro lado, para caracterizar el funcionamiento de la articulación también se utiliza el mismo instrumento de medición. De este modo, con el palpador de la MMC se mide la posición alcanzada por el del brazo y se comparan las coordenadas que proporcionan ambos métodos obtenidas con respecto al mismo sistema de referencia, ya que previamente se llevan a cabo los pasos necesarios para hacerlos coincidir.

La captura de las lecturas de los encoders angulares y su transformación, mediante la implementación del modelo geométrico, a coordenadas cartesianas del punto medido se lleva a cabo mediante un software desarrollado también específicamente.

Los resultados obtenidos inicialmente indican que las incertidumbres de medición en los tres ejes son las que se muestran en la tabla 1.

Tabla 1. Incertidumbres iniciales

Las incertidumbres representadas en la tabla 1 son las globales en cada eje, es decir, las máximas de entre todos los puntos de medición del ensayo. Dichas incertidumbres en cada punto y en cada eje se calculan a partir de la propia del instrumento patrón (MMC) y de las desviaciones típicas de las mediciones.

La determinación de los parámetros geométricos mediante medición es un aspecto crítico del proceso. Durante él mismo se comprueba que existe una gran variabilidad en los resultados de estos parámetros, principalmente debido a que resulta difícil restringir totalmente los movimientos del brazo durante su medición con la MMC.

Para obtener unos parámetros más ajustados se recurre a un proceso de optimización secuencial de los mismos. Su objetivo es minimizar el error medio de las coordenadas proporcionadas por el brazo con respecto a las de la MMC. Para ello se varía secuencialmente el valor de los parámetros en un número de puntos dentro de un intervalo establecido. Con cada combinación de los nuevos parámetros se vuelve a calcular el error medio. Si es menor que el de la etapa anterior se considera que los nuevos parámetros son mejores que los anteriores y se continúa el proceso de optimización con ellos. Tras llevar a cabo este proceso las nuevas incertidumbres obtenidas se muestran en la tabla 2.

Tabla 2. Incertidumbres optimizadas

Dada la resolución de los encoders (5.000 pasos por revolución multiplicados por cuatro en la tarjeta capturadora) estos resultados son razonables si se comparan con los esperados por simulación obtenidos a partir del modelo geométrico al introducir en él valores nominales de los parámetros.

Conclusiones

Los resultados obtenidos y los procedimientos desarrollados para la confección del modelo geométrico y del algoritmo de optimización permiten pensar en la posibilidad de desarrollar procedimientos de calibración [2] destinados a la determinación de las correcciones e incertidumbres necesarias y a la mejora y optimización general de estos sistemas.

[1] K.S. Fu, R.C. González y C.S.G. Lee, Robótica: control, detección, visión e inteligencia, MacGraw Hill, (1988)
[2] Hans Norgaard Hansen; Verification and calibration of co-ordinate measuring machines, Technical University of Denmark, (1997).