Comparación de las diferentes normas para el cálculo de incertidumbre de medición en Tomografía Computarizada

Este trabajo se presentó en el Congreso de Metrología de 2017

La Tomografía Computarizada (TC) ha irrumpido en el campo de la metrología industrial como una nueva técnica de verificación dimensional que permite ser una alternativa a la medición mediante Máquinas de Medir por Coordenadas (MMCs) tanto de tipo táctil, como óptico [1]. La principal ventaja que ofrece esta tecnología sin contacto frente a las técnicas tradicionales es la posibilidad de caracterización de geometrías tanto externas como internas o sin accesibilidad, sin la necesidad de destruir o seccionar una pieza de trabajo. De este modo, es posible llevar a cabo análisis de, por ejemplo, componentes producidos por fabricación aditiva, los cuales cuentan con características internas que no son accesibles a la vista o que se componen de diferentes materiales [2,3]. Sin embargo, a pesar de ser la única tecnología capaz de medir geometrías internas, la TC presenta algunas limitaciones muy significativas. La principal problemática reside en el elevado número y complejidad de las fuentes de error y/o incertidumbre que afectan al proceso de medición [4,5]. Estos errores son debidos a causas de diferente índole, que abarcan tanto al propio hardware, software, pieza de trabajo, operador y condiciones ambientales. Por ese motivo, dada la reciente aplicación metrológica de la TC, aún no existen procedimientos normalizados y ampliamente aceptados para establecer una aproximación confiable del cálculo de la incertidumbre de medida. Son muchos los enfoques que se han planteado a la cuestión de estimación de la incertidumbre de medida con sistemas de TC. Muchos resultados provienen de métodos basados en la aplicación directa de la guía para la expresión de la incertidumbre de medida (GUM) [6] e ISO 14253-2 [7]. Otros autores han considerado los métodos de simulación de la variabilidad, tales como el método de Monte Carlo [8]. Diferentes trabajos han basado el cálculo de incertidumbres con TC en base a la estimación de la variabilidad sistemática y estocástica de forma experimental, adaptando, por ejemplo, la norma ISO 15530-3 [9]. En la actualidad se ha extendido el uso de una adaptación de la norma ISO 15530-3 para Tomografía Computarizada, tal y como se recoge en el estándar alemán VDI 2630-2.1 [10]. No obstante, este cálculo de incertidumbre sólo es posible utilizando mediciones de una pieza similar realizadas con otros equipos de medición 3D, lo cual no siempre es factible. La necesidad de caracterización previa mediante métodos tradicionales impide la caracterización de geometrías internas, por lo que la principal aplicación de la TC no quedaría contemplada en base a este procedimiento.

Basado en la anterior motivación, este trabajo comienza presentando un análisis comparativo entre las diferentes normas consideradas, describiendo sus principales ventajas e inconvenientes sobre su idoneidad de uso para su aplicación en TC. Tras dicho análisis, y para el caso de una pieza micro-inyectada (con dimensiones de muy pocos milímetros), se comparan los resultados de incertidumbre obtenidos en el caso de caracterización con una MMC óptica, la aplicación de la norma más aceptada actualmente y específica para TC (VDI 2630-2.1 [10]) y un método alternativo propuesto que no requiere de la calibración previa de la pieza de trabajo. Esta alternativa para la estimación de la incertidumbre de medida que se presenta, aplica la norma ISO 14253-2 [7] considerando un valor de error máximo permitido (maximum permissible error, MPE) global del sistema de medida, suficientemente representativo para asegurar la trazabilidad del resultado, el cual se ha determinado con diferentes ítems calibrados de varias geometrías, materiales y dimensiones.

La tomografía computarizada es una técnica no destructiva de medición que parte de un volumen con alta densidad de puntos. Al basarse en la emisión y recepción de rayos X, es capaz de determinar geometrías internas y externas con un tiempo de adquisición relativamente corto. Sin embargo, como se justifica a continuación, su principio de medida y las fases necesarias traen consigo un número elevado de fuentes de error que dificultan la definición de un proceso normalizado para el cálculo de la incertidumbre de medida.

2.1 Principio de medida TC

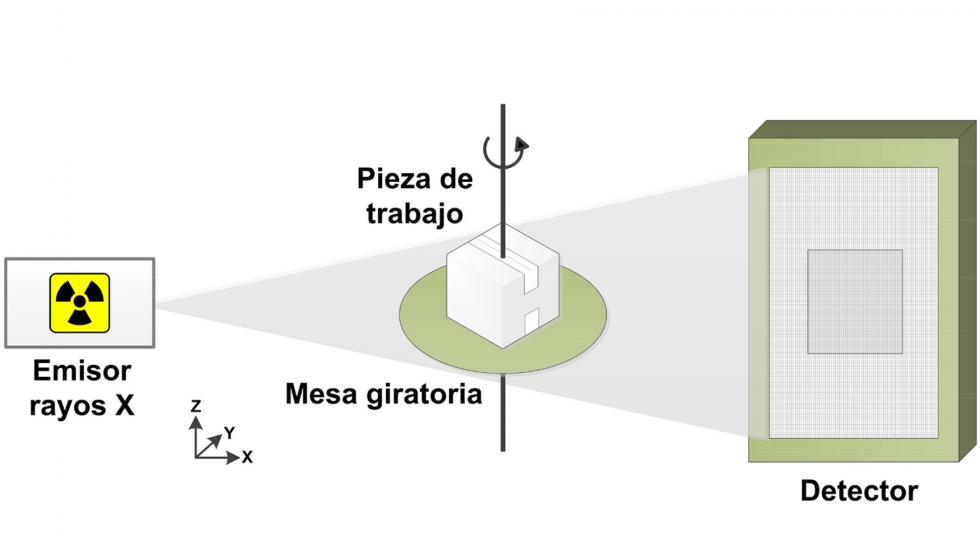
La TC, y más específicamente la micro Tomografía Computarizada con haz cónico, tiene tres elementos principales (ver figura 1): un emisor de rayos X, una mesa giratoria y un detector. La radiación electromagnética producida por la fuente incide sobre la pieza de trabajo que se localiza sobre la mesa giratoria. Al atravesar el objeto, los rayos X emitidos son atenuados y detectados por el sensor, de forma que se genera una imagen bidimensional (2D). Gracias al giro de la mesa, se toman diferentes imágenes de la pieza en estudio, cuyas proyecciones son analizadas para generar un modelo tridimensional (3D) de la misma.

2.2 Fases en TC para aplicaciones de metrología dimensional

El proceso habitual de medición mediante TC establece las siguientes fases. En primer lugar, se captura el conjunto de imágenes procedentes del detector utilizado en las diferentes posiciones de giro de la mesa. En segundo lugar, a través de las imágenes capturadas segenera mediante reconstrucción el modelo 3D de la pieza de trabajo, con información relativa a la atenuación que genera a los rayos X cada punto del volumen de medición. La tercera etapa de segmentación traduce la información del nivel de gris de cada uno de los elementos del volumen 3D en el borde o límites de la pieza, utilizando algoritmos de extracción de superficie. Finalmente, a partir del modelo de superficie obtenido, nube de puntos, etc., es posible determinar los resultados de medición requeridos.

2.3 Fuentes de error en TC

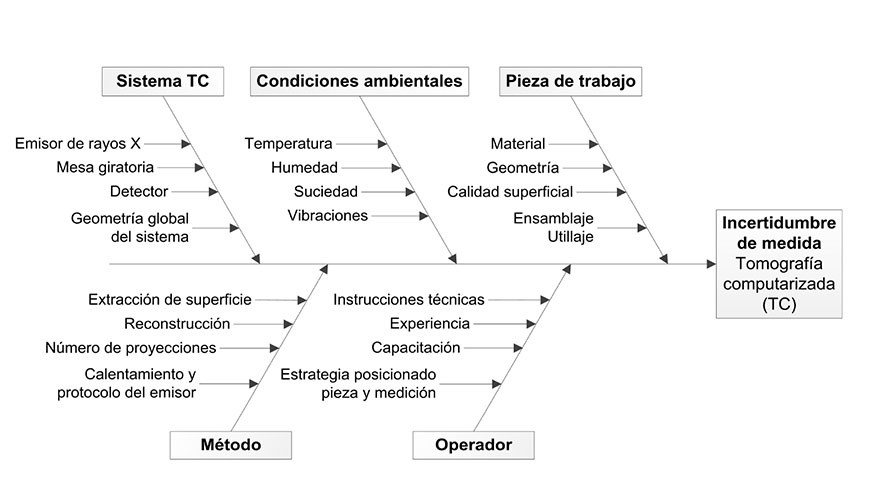
Dados los diferentes elementos que conforman un sistema de medida de TC y las fases requeridas para llevar a cabo la caracterización dimensional de piezas, la medición con tomografía computarizada se caracteriza por estar afectada por multitud de fuentes de error. En la literatura las diferentes causas de incertidumbre se clasifican en relación a diferentes criterios [1,5]. En este trabajo, dichos factores de influencia se esquematizan en la figura 2.

La discusión de los procedimientos disponibles para la evaluación de la incertidumbre de medida con TC se ha presentado en diferentes referencias previas [1, 11, 12]. Nuevos estándares internacionales han ido apareciendo y también han de ser considerados. Otros se encuentran todavía en vías de desarrollo. Los procedimientos normalizados que se usan con MMCs de tipo táctil u óptico no pueden ser aplicados de forma directa debido al método y estrategia de medición de TC. No obstante, organizado por la Universidad de Padua, se llevó a cabo una intercomparación entre laboratorios que proponía a los participantes la evaluación de la incertidumbre de medida de cuatro artefactos calibrados (diferentes geometrías, materiales y dimensiones) para analizar los métodos de cálculo elegidos por los participantes y sus resultados obtenidos [13,14]. Las conclusiones demostraron que no existía un criterio común claro para el cálculo de incertidumbre con TC, y que los participantes tenían grandes dificultades para asegurar la trazabilidad de las medidas, incluso siendo usuarios expertos.

Igualmente, la falta de procedimientos establecidos se une a la dificultad de establecimiento de objetos de referencia. Artefactos con esferas patrón (e.g. barras de bolas) permiten determinar la distancia entre centros e identificar el factor de escala. La medición de la posición entre centros de esferas no está influenciada por los diversos factores que afectan a las imágenes escaneadas (detección de bordes, umbral, desplazamiento de la superficie, etc.). Otras referencias de medidas longitudinales como bloques patrón o pirámides escalonadas con dimensiones conocidas sirven para definir el tamaño de píxel o voxel con la unidad de longitud.

Sin embargo, el material, geometría y demás condiciones afectan a la medida y de allí que tampoco existan patrones de referencia definidos. A continuación, se resumen y describen los diferentes métodos utilizados para el cálculo de incertidumbre con TC. Muchos de ellos se apoyan en las normas internacionales que consideran MMCs. Solamente la VDI 2630-2.1 se considera el caso específico de sistema de medida de TC. Otros procedimientos son combinaciones de los métodos mencionados anteriormente y consecuencia de la experiencia.

3.1 Cálculo de incertidumbres basado en modelos de medición

Los métodos de cálculo basados en la aplicación directa de la guía para la expresión de la incertidumbre de medida (GUM) [6] e ISO 14253-2 [7] necesitan el modelo matemático de la medición y la aplicación de la ley de propagación de errores. Para los sistemas de TC, la problemática de estas normas reside en la complejidad del proceso de medición, los numerosos factores de influencia, su compleja cuantificación e interacción, y su variabilidad en el tiempo. Una solución analítica para describir la incertidumbre de medición supone un trabajo complejo que puede resultar inviable. En esta línea, sólo se han analizado enfoques simplificados del problema de medida en diferentes trabajos:

• Según la GUM [6], se ha evaluado la influencia de la orientación de la pieza de trabajo, magnificación y número de proyecciones [15] y la incertidumbre asociada al número y tamaño de voxel [16].
• El método iterativo y simplificado de acuerdo con la norma ISO 14253-2 [7] tiene un uso más extendido y es el considerado en [17,18].

3.2 Métodos basados en la simulación de la variabilidad

Los métodos numéricos como el método de Monte Carlo [8] basan su cálculo de incertidumbre en las funciones de distribución de probabilidad de las diferentes fuentes de error consideradas, por lo que deben ser completos y los factores no incluidos en el modelo también deben estimarse por otros medios. Además, los resultados tienen que ser validados experimentalmente. Debido a la complejidad de las mediciones con TC (gran número de parámetros de influencia) y el coste computacional de la simulación, han sido escasos los intentos de evaluación de incertidumbres con este enfoque:

• Una máquina TC virtual se ha desarrollado en [5] para estudiar las influencias en la calidad de la imagen y la geometría de la pieza escaneada mediante el modelado numérico de las proyecciones del haz de rayos X.
• Otro método de simulación se ha presentado en [19], basado en Monte Carlo pero que presenta mayores ventajas en la estimación de incertidumbres.

3.3 Métodos basados en el uso y medición previa de piezas de trabajo calibradas

Los métodos empíricos según ISO 15530-3 [9] y la norma específica para TC VDI 2630-2.1 [10] se basan en la evaluación de la incertidumbre de medición mediante el uso de una pieza similar a la que se analiza que se encuentre previamente calibrada. Esta calibración realizada con otros equipos de medición tridimensional no siempre es factible. Del mismo modo, otro inconveniente que aparece con este procedimiento es la pérdida de la capacidad de caracterización de características internas, ventaja más prometedora de los sistemas de tomografía computarizada. Sólo pueden medirse de este modo geometrías exteriores y usando la misma estrategia y condiciones durante el proceso que en el caso de caracterización de la pieza de trabajo a inspeccionar. A pesar del gran número de experimentos de repetición necesarios para la validación, este procedimiento está considerado actualmente como el más aceptado para la evaluación de incertidumbres con TC:

• La norma ISO 15530-3 [9] se ha aplicado en las referencias [12,20–22].
• El estándar alemán VDI 2630-2.1 [10] que se publicó en Junio se publicó 2015 y que considera las medidas externas realizadas con sistemas específicos de TC aparece considerado en [23].

El análisis previo realizado sobre las diferentes normas aplicables al cálculo de incertidumbres de medida con sistemas de tomografía computarizada concluye con la necesidad de definición de un procedimiento acorde a la tecnología utilizada. El elevado número de fuentes de influencia hace que los métodos de cálculo mediante el uso del modelo de medición y los métodos numéricos basados en simulación sean difíciles de abordar. Igualmente, la limitación de la norma VDI 2630-2.1 sólo aplicable a geometrías externas deja patente la necesidad de un nuevo enfoque para la evaluación de la incertidumbre mediante TC. Así, el método que a continuación se presenta trata de obtener un procedimiento que no requiera la caracterización previa de piezas similares con un sistema de medición más preciso permitiendo así la medición de geometrías internas, geometrías tridimensionales complejas 3D, etc. El método se basa en la estimación del error máximo permitido (MPE) del sistema de TC, determinado experimentalmente mediante varios artefactos calibrados de referencia. El objetivo es, por tanto, disponer de un valor global y de fácil aplicación en el cálculo que asegure la trazabilidad de la medición.

4.1 Procedimiento MPE

El cálculo de la incertidumbre expandida en base al procedimiento alternativo que aquí se presenta se realiza de acuerdo a la norma 14253-2 [7], considerando las fuentes de error específicas que recoge la versión vigente de la VDI 2630-2.1 [10]:

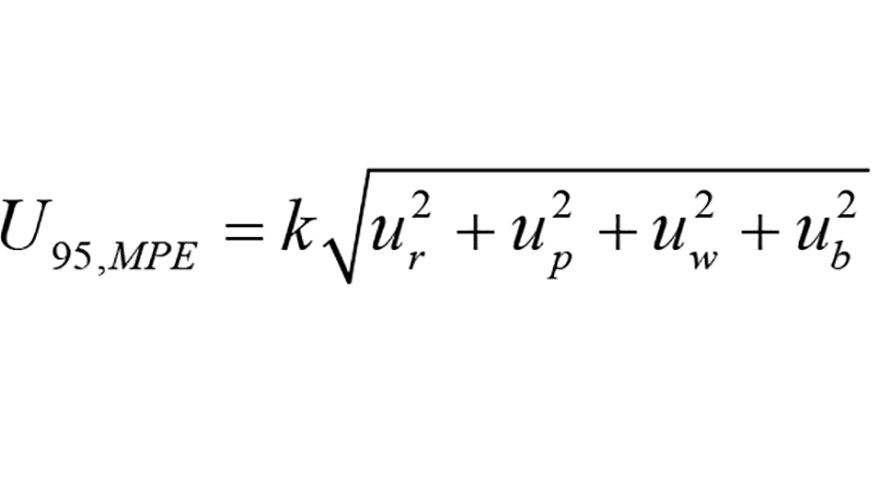
El término k es el factor de cobertura (k=2), ur es la varianza asociada al MPE estimado, up es la varianza asociada a la repetibilidad del método, uw es la varianza asociada derivada de desviaciones en la pieza de trabajo y ub es la varianza asociada al error sistemático. En particular, el término del error máximo permitido es igual a MPE = 6.6 µm + (L/5.4) µm, L en mm. Este valor considera no sólo la influencia de diferentes geometrías, tamaños, materiales, posiciones y orientaciones de estos patrones de referencia, sino también la reproducibilidad de los parámetros de operación, procesamiento de datos y condiciones ambientales, por lo que se considera suficientemente representativo y conservador.

Para validar los resultados que se obtienen con el método planteado la pieza de trabajo que a continuación se presenta se ha considerado:

• La medición previa de la pieza de trabajo con un sistema de medir por coordenadas óptimo (denominado como MMCO).
• El cálculo de incertidumbres obtenido tras la aplicación de la norma VDI 2630-2.1, mayormente aceptada por la comunidad científica.

4.2 Pieza en estudio

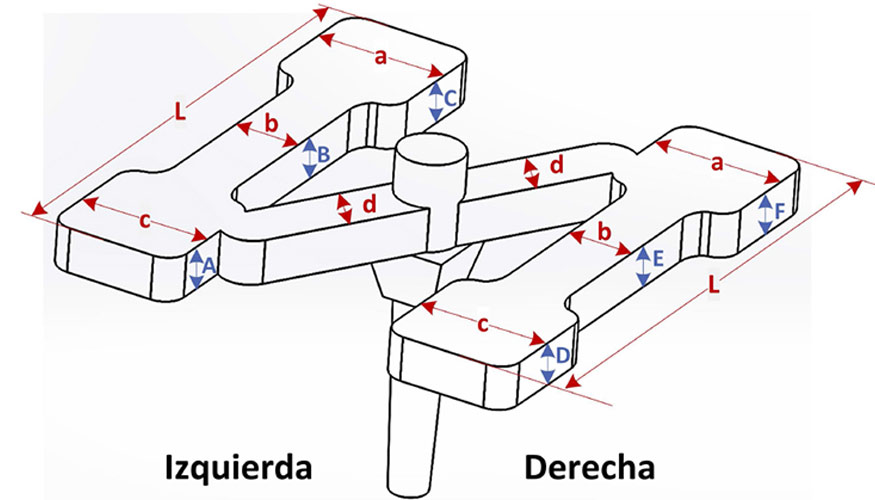
La pieza de trabajo que se ha caracterizado se muestra en la figura 3. Se denomina ‘Dog Bone’, ha sido fabricada en Polioximetileno de Acetal (POM) y se utiliza para aplicaciones micromecánicas. Sus dimensiones de interés son las siguientes: la anchura de la pieza en ocho zonas distintas (a, b, c, d); la longitud de los dos cuerpos laterales (L); y los seis espesores de los dos cuerpos laterales (A, B, C, D, E, F).

4.3 Resultados de incertidumbre obtenidos

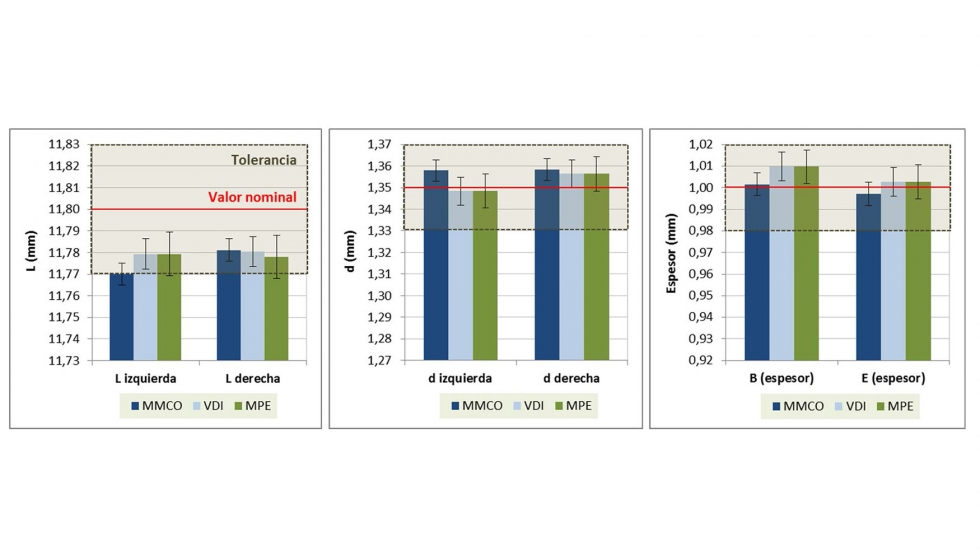
Los resultados de incertidumbre obtenidos se muestran en la figura 4, donde se comparan tanto los resultados con la MMCO, los de aplicación de la noma VDI 2630-2.1 y los obtenidos tras la consideración de la alternativa de cálculo con el MPE global del sistema de TC. Se muestra, en particular, el caso de los parámetros d (anchura, d=1,35±0,02 mm), L (longitud, L=11,80±0,03 mm) y B y E (espesores, B, E=1,00±0,02 mm) de una de las cuatro piezas que se han evaluado y que se considera como representativa de dicha muestra. Como técnica de extracción de superficies para los resultados con TC, para la identificación del valor de umbral se ha utilizado el método del ISO 50%.

Tal y como se representa en la figura 4, los resultados obtenidos mediante los tres procedimientos son similares. En términos de incertidumbre, el nuevo procedimiento basado en el MPE es prácticamente análogo al obtenido mediante la norma VDI 2630-2.1. La máquina de medir por coordenadas óptica destaca como sistema más preciso, aunque su resultado de incertidumbre podría parecerse más al obtenido mediante el nuevo procedimiento si el ajuste del MPE se hace de forma menos conservadora. Igualmente, en la figura 4 se muestra el valor nominal de cada parámetro y su rango de aceptación. Según lo observado, los tres procedimientos aseguran la tolerancia micrométrica especificada, resultando comparables.

La Tomografía Computarizada, a pesar de sus importantes ventajas metrológicas, todavía presenta limitaciones a la hora de establecer una aproximación confiable en el cálculo de la incertidumbre de medida. Los procedimientos que requieren del modelo de medición o la simulación por métodos numéricos de las fuentes de influencia son imprecisos dado el elevado número de factores a considerar. Modelos que necesitan de una pieza de referencia previamente calibrada, aunque son los más aceptados, no permiten la caracterización de geometrías internas o complejas. Como solución, este trabajo ha planteado un método de cálculo de incertidumbre basado en el MPE del sistema que, de acuerdo a los resultados obtenidos, podría tener aplicabilidad en la prometedora técnica de medición mediante TC.

Referencias

[1] J.P. Kruth, M. Bartscher, S. Carmignato, R. Schmitt, L. De Chiffre, A. Weckenmann, Computed tomography for dimensional metrology, CIRP Ann. - Manuf. Technol. 60 (2011) 821–842.

[2] L. De Chiffre, S. Carmignato, J.-P. Kruth, R. Schmitt, A. Weckenmann, Industrial applications of computed tomography, CIRP Ann. - Manuf. Technol. 63 (2014) 655–677.

[3] F. Borges de Oliveira, A. Stolfi, M. Bartscher, L. De Chiffre, U. Neuschaefer-Rube, Experimental investigation of surface determination process on multi-material components for dimensional computed tomography, Case Stud. Nondestruct. Test. Eval. 6 (2016) 93–103.

[4] V. Andreu, B. Georgi, H. Lettenbauer, J.A. Yague, Analysis of the error sources of a Computer Tomography Machine, in: Proc. Lamdamap Conf., 2009: pp. 462–471.

[5] J. Hiller, L.M. Reindl, A computer simulation platform for the estimation of measurement uncertainties in dimensional X-ray computed tomography, Measurement. 45 (2012) 2166–2182.

[6] Guide to the Expression of Uncertainty in Measurement (GUM), (2008).

[7] ISO 14253-2:2011. Geometrical product specifications (GPS). Inspection by measurement of workpieces and measuring equipment. Part 2: Guidance for the estimation of uncertainty in GPS measurement, in calibration of measuring equipment and in product verification, (2011).

[8] Evaluation of measurement data — Supplement 1 to the “Guide to the expression of uncertainty in measurement” — Propagation of distributions using a Monte Carlo method, JCGM 101:2 (2008).

[9] ISO 15530-3. Geometrical product specifications (GPS). Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement. Part 3: Use of calibrated workpieces or measurement standards, (2011).

[10] VDI/VDE 2630 Part 2.1 Determination of the uncertainty of measurement and the test process suitability of coordinate measurement systems with CT sensors, (2015).

[11] M. Bartscher, M. Neukamm, U. Hilpert, U. Neuschaefer-Rube, F. Härtig, K. Kniel, K. Ehrig, A. Staude, J. Goebbels, Achieving Traceability of Industrial Computed Tomography, Key Eng. Mater. 437 (2010) 79–83.

[12] R. Schmitt, C. Niggemann, Uncertainty in measurement for x-ray-computed tomography using calibrated workpieces, Meas. Sci. Technol. 21 (2010) 54008.

[13] S. Carmignato, A. Pierobon, P. Rampazzo, M. Parisatto, E. Savio, CT for Industrial Metrology – Accuracy and Structural Resolution of CT Dimensional Measurements, Conf. Ind. Comput. Tomogr. (2012) 161–172.

[14] S. Carmignato, Accuracy of industrial computed tomography measurements: Experimental results from an international comparison, CIRP Ann. - Manuf. Technol. 61 (2012) 491–494.

[15] A. Weckenmann, P. Krämer, Assessment of measurement uncertainty caused in the preparation of measurements using computed tomography, in: 19th IMEKO World Congr. 2009, Quality Management and Manufacturing Metrology, University Erlangen-Nuremberg, Erlangen, Germany, 2009: pp. 1787–1791.

[16] W. Dewulf, K. Kiekens, Y. Tan, F. Welkenhuyzen, J.P. Kruth, Uncertainty determination and quantification for dimensional measurements with industrial computed tomography, CIRP Ann. - Manuf. Technol. 62 (2013) 535–538.

[17] P. Müller, A. Cantatore, J.L. Andreasen, J. Hiller, L. De Chiffre, Computed tomography as a tool for tolerance verification of industrial parts, in: Procedia CIRP, 2013: pp. 125–132.

[18] A. Stolfi, M.K. Thompson, L. Carli, L. De Chiffre, Quantifying the Contribution of Post- Processing in Computed Tomography Measurement Uncertainty, Procedia CIRP. 43 (2016) 297–302.

[19] J. Hiller, G. Genta, G. Barbato, L. De Chiffre, R. Levi, Measurement uncertainty evaluation in dimensional X-ray computed tomography using the bootstrap method, Int. J.Precis. Eng. Manuf. 15 (2014) 617–622.

[20] D. Chiffre, P. Müller, J. Hiller, A. Cantatore, L. De Chiffre, L. De Chiffre, A study on evaluation strategies in dimensional X-ray computed tomography by estimation of measurement uncertainties, Int. J. Metrol. Qual. Eng. 3 (2012) 107–115.

[21] J. Hiller, M. Maisl, L.M. Reindl, Physical characterization and performance evaluation of an x-ray micro-computed tomography system for dimensional metrology applications, Meas. Sci. Technol. 23 (2012) 85404.

[22] P. Müller, J. Hiller, Y. Dai, J.L. Andreasen, H.N. Hansen, L. De Chiffre, Estimation of measurement uncertainties in X-ray computed tomography metrology using the substitution method, CIRP J. Manuf. Sci. Technol. 7 (2014) 222–232.

[23] A. Kraemer, G. Lanza, Assessment of the Measurement Procedure for Dimensional Metrology with X-ray Computed Tomography, Procedia CIRP. 43 (2016) 362–367.

Agradecimientos

Este trabajo ha sido financiado por el proyecto de investigación DPI2015-69403-C3-1-R (MINECO) y por el proyecto UZCUD2016-TEC-09 (Universidad de Zaragoza y Centro Universitario de la Defensa Zaragoza). Asimismo, agradecer al departamento de Ingeniería Mecánica de la DTU (Technical University of Denmark) su colaboración.