Sencillo algoritmo para seleccionar los puntos significativos tras un escaneo de un perfil o de una superficie

Después de digitalizar un perfil o una superficie se dispone de un elevado número de coordenadas de puntos agrupados según la estrategia seguida para la digitalización [1]. Pero no todos los puntos tienen el mismo peso. En las zonas donde la curvatura es grande se precisan más puntos que donde es pequeña [2]. Aquí se presenta un método sencillo, basado en el cálculo de un ángulo o de un coseno, que permite seleccionar los puntos que aportan información significativa para la reconstrucción de la forma mediante un programa de CAD o su mecanizado en una máquina de CN. Para ello se ha usado el programa Matlab, pero igualmente se puede realizar desde Excel con una macro en Visual Basic.

Hay varios métodos para digitalizar un perfil o una superficie:

• Utilizando una fresadora de CN con un palpador acoplado a su cabezal.
• Con la máquina de medir de coordenadas. El sistema es semejante al anterior pero con más precisión.
• Sustituyendo el palpador mecánico de la máquina de coordenadas por un láser [3].
• Utilizando directamente un mecanismo Láser Tracker.

En todos los casos cuando el número de puntos escaneado en muy alto conviene realizar un filtrado de los mismos para descartar aquellos que aportan menor peso para la identificación de la forma digitalizada.

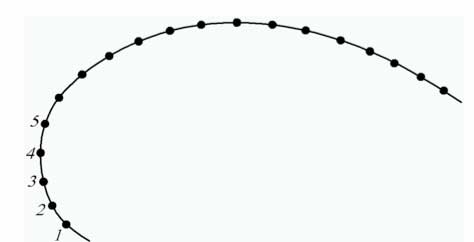
Los puntos que aportan más peso son los situados en las zonas de más curvatura y los que menos los situados en las zonas de menor curvatura. En la figura 1 se muestra un perfil aerodinámico.

Seguidamente se va a describir un sencillo algoritmo para utilizar solamente los puntos más significativos o que aportan más peso al trazado de una curva, con ello, además de la limpieza del proceso de reconstrucción se va a ganar en velocidad de proceso en el sistema informático.

Figura 1. Viendo el peine de curvatura, los puntos de tramo próximos al borde de ataque aportan más peso a la gráfica.

Figura 2. Simulación de un escaneado de puntos en el extradós de un perfil aerodinámico en el intervalo {0, 1} en pasos de 0.01.

Figura 3. El polígono de la derecha se aproxima mejor a la circunferencia.

En el desarrollo de nuestras experiencias mecanizando hélices de aeromodelos, observamos que sería interesante disponer de un algoritmo que seleccionara la cantidad y calidad de los puntos obtenidos tras escanear una superficie con la máquina de coordenadas.Observando la figura 1, correspondiente a un perfil aerodinámico [5], se llega a la conclusión de que en las proximidades del borde de ataque serán precisos más puntos para su definición que en puntos del extradós. Ello es debido a que la curvatura en el primero es mayor que en segundo, como se aprecia al observar al peine de curvatura representado.

En la figura 2 se ha dibujado una simulación de posibles puntos de escaneo realizando una variación constante en el eje cordal del perfil. Obviamente, como se analizará a continuación, no son precisos todos los puntos para definirlo con una precisión requerida.

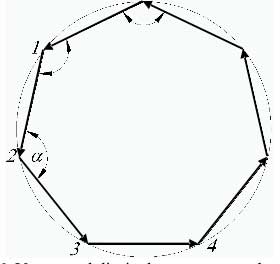
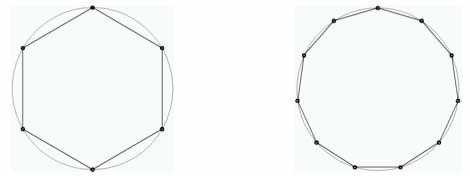
En la figura 4 se muestran dos circunferencias, con dos aproximaciones poligonales. Cuantos más lados tiene el polígono más aproximado será éste a la circunferencia.

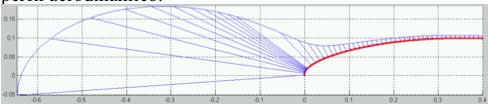
Se observa que en el caso de la figura 3 el paso de 0.01 es amplio para la zona próxima al borde de ataque mientras que para el resto es estrecho. Ello significa que, en un escaneado continuo, debemos utilizar un paso muy reducido. ¿Pero qué hacer con los puntos obtenidos? Seguidamente veremos que se pueden filtrar con un simple algoritmo que se puede realizar en Excel o Matlab y quedarnos con un número muy inferior de puntos que serán más fáciles de manipular en la reconstrucción de la pieza.

La relación que hay entre el número de segmentos de la poligonal que aproxima la circunferencia y el error cometido en la figura 4 se puede deducir fácilmente de la figura 5, donde e representa el error cordal.

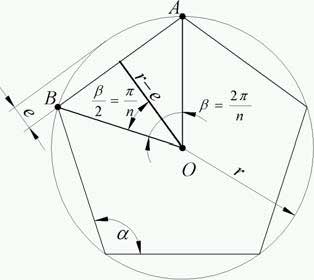
Por otro lado, el ángulo que forman los lados del polígono está relacionado con el ángulo ≤ que forman los radios por:

Es decir, el error finalmente está relacionado con el coseno del ángulo ≤/2, el cual a su vez se puede obtener a partir del ángulo que forman las cuerdas o lados del polígono que aproximan la circunferencia.

Si ahora los lados del polígono los convertimos en vectores, figura 6, resulta que el ángulo que forman los lados esta definido por el producto escalar de los vectores:

Como se ha indicado en la figura 6, los puntos que delimitan los vectores pueden corresponder a puntos escaneados. Pues, a la vista de la figura 7, si los puntos escaneados están lo suficientemente próximos, cada tres puntos determinan una circunferencia. Así, tendremos las circunferencias definidas por los puntos (1, 2, 3), (2, 3, 4) y así sucesivamente.

De esta forma es posible preparar un algoritmo que estudie los puntos (1, 2, 3), si el coseno dado por la expresión (*) es superior a un valor podemos descartar el punto intermedio 2. Si no se descarta este punto, se pasa a verificar los puntos (2, 3, 4). En el caso de desechar el punto 2, se pueden dar varias posibilidades de continuar con el algoritmo:

a) Repetir lo anterior con los puntos (1, 3, 4) y así sucesivamente. El punto que se puede ahora desechar es el 3.

b) Realizar el algoritmo con los puntos (3, 4, 5). Siendo el objetivo desechar o no el punto 4.

Tras diversas comprobaciones, la variante que mejor resultado ha dado es la segunda. En cuyo caso se ha optado por repetir el algoritmo total hasta que no aparece ningún punto a descartar.

El algoritmo se muestra comentado en el siguiente listado de Matlab. Entre las líneas 13 y 17 el programa lee las coordenadas de los puntos escaneados. En la línea 28 se realiza el producto escalar y los módulos de los vectores con las funciones disponibles para ello en Matlab.

Figura 4. Principio matemático

El programa anterior se ha aplicado a puntos de la función para diversos incrementos de la variable independiente x. Así, es posible realizar un text sobre la validez del algoritmo explicado

Para terminar, el algoritmo también se ha aplicado a un perfil escaneado de hélice de aeromodelismo. El resultado se muestra en la figura 9

De la observación de los resultados se llega a las siguientes conclusiones:

• En las zonas donde la curvatura es reducida prácticamente coincide el número de puntos que la define aunque aumentemos la precisión (disminución del paso) del escaneado.
• El número de puntos de definición, para una precisión de coseno dada, aumenta en la zona de más curvatura a medida que disminuimos el paso de escaneo.
• A partir de una disminución de paso de escaneo (aumento de la precisión para definir el perfil) el número de puntos converge para una precisión de coseno dada.
• El procedimiento se ha mostrado válido para un escaneo con MMC, como se vio en la figura 9

El algoritmo presentado también es posible implementarlo sobre el propio programa de medición en la MMC. De tal manera que el paso de escaneo se adapte a la curvatura. Con ello se puede mejorar el tiempo de utilización de la MMC cuando el escaneo es punto a punto (en continuo bastará con aplicar el algoritmo a la tabla de puntos obtenida).

El algoritmo se pude utilizar para detectar imperfecciones puntuales, al detectar cambios bruscos en la curvatura. Con lo que se desecharían los puntos que están en el intervalo de cambio de dicha curvatura, figura 9

También es posible utilizar el algoritmo para obtener los puntos de mecanizado de una función conocida. Con ello no sería necesario conocer las derivadas primera y segunda de la función.

[1] M.W. Cho, T.I. Seo. Inspection Planning Strategy for the On-Machine Measurement Process Based on CAD/CAM/CAI Integation.

[2] J.L. Huertas, F. Torres, F. Floren, V. Hernández. Obtaining a Program of Mechanizing of an Aerodynamic Profile Using Matlab. The International Journal of Advanced Manufacturing Technology. ¿?2005, 19:607-617

[3] F.J. Shiou, T. Pfeifer. Strategies and Processes to Measure the Dimensional Geometry of Sheet Metal Parts for Exact Laser Cutting. The International Journal of Advanced Manufacturing Technology. 2002, 19:106-116.

[4] H.W. Corley, Jay Rosenberger, Wei-Chang Yeh, T.K. Sung. The cosine simplex algorithm. The International Journal of Advanced Manufacturing Technology. 2005, 10:106-116.

[5] E.N. Jacobs. K.E. Ward, R.M. Pinkerton. The characteristics of 78 related airfoil sections form tests in the variable-density wind tunnel. Report nº 460. NACA.

[6] Solid Edge the CAD 3D of EDS.

Figura 5. Vectores delimitados por puntos de escaneo.

Figura 6. Sucesión de puntos escaneados